
中值定理 第二章我们讨论了微分法,解决了曲线的切线、 法线及有关变化率问题。这一章我们来讨论导数的 应用问题。 我们知道,函数y=f(x)在区间<x,x,+c> 上的增量y=f(x,+x)-f(x)可用它的微分 少=f'(x)△k来近似计算其误差是比x 高阶的无穷小 即 4少≈f',)是近似关系(充分小
中值定理 第二章我们讨论了微分法,解决了曲线的切线、 法线及有关变化率问题。这一章我们来讨论导数的 应用问题。 我们知道,函数 ( ) ( ) 0 x0 y = f x + x − f y = f (x) 在区间 x0 , x0 + x 上的增量 可用它的微分 dy = f (x0 )x 来近似计算 其误差是比 x 高阶的无穷小 ( ) x0 f x y 即 是近似关系 (| x |充分小)

而im 少=f(x)是极限关系,都不便应用 c-→0 我们的任务是寻求差商与导数的直接关系,既 不是极限关系,也不是近似关系。对此,Lagrange 中值定理给出了圆满的解答: Ay=f(xo+04x)Ax 导数应用的理论基础 本章我们先给出Rolle定理(它是Lagrange定 理的特殊情况),由特殊过渡到一般来证明 Lagrange定理和Cauchy定理,有了Cauchy定理 就可以给出Taylor中值定理及L,Hospital法则, 这就是本章理论部分的主要内容
lim ( ) 0 0 f x x y x = → 而 是极限关系,都不便应用 我们的任务是寻求差商与导数的直接关系,既 不是极限关系,也不是近似关系。对此,Lagrange 中值定理给出了圆满的解答: y = f (x0 +x)x ——导数应用的理论基础 本章我们先给出Rolle定理(它是Lagrange定 理的特殊情况),由特殊过渡到一般来证明 Lagrange定理和Cauchy定理,有了Cauchy定理 就可以给出Taylor中值定理及L, Hospital法则, 这就是本章理论部分的主要内容
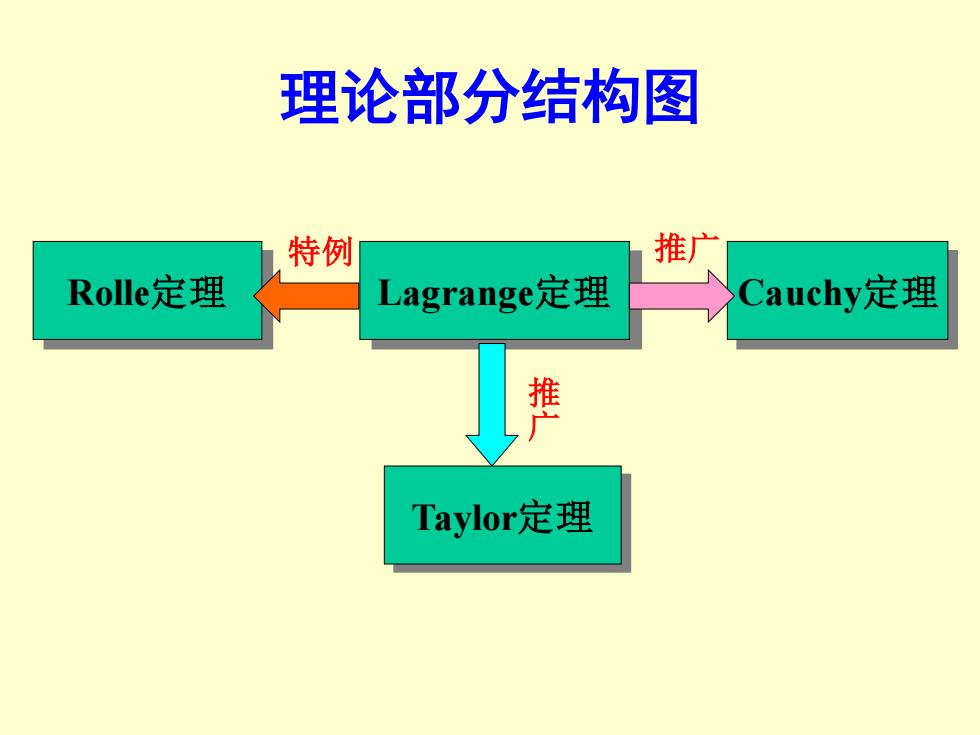
理论部分结构图 特例 推广 Rolle定理 Lagrange定理 Cauchy定理 推 Taylor定理
理论部分结构图 Lagrange定理 特例 Rolle定理 推广 Cauchy定理 推 广 Taylor定理

本章的导数应用部分就是以此为基础展开讨论 的,利用Lagrange定理给出了可导函数的单调性和 凹凸性的判定法则,可以讨论可导函数取得极值的 条件;有了L'Hospital法则,可以进一步讨论 0'00-0,0-o,0,co',1 000 等各种类型的未定式的极限;此外利用中值定理和 单调性还可证明一些不等式。 重点 微分中值定理 L,'Hospital法测 Taylor公式 求函数的极值和最值
本章的导数应用部分就是以此为基础展开讨论 的,利用Lagrange定理给出了可导函数的单调性和 凹凸性的判定法则,可以讨论可导函数取得极值的 条件;有了L, Hospital法则,可以进一步讨论 − , ,0 , ,0 , ,1 0 0 0 0 等各种类型的未定式的极限;此外利用中值定理和 单调性还可证明一些不等式。 重点 微分中值定理 L, Hospital法则 Taylor公式 求函数的极值和最值

维点 中值定理 L'Hospital法则的运用 利用中值定理证明不等式 基车要求 ①正确理解和掌握R、L、C、T定理及它们之 间的关系 ②熟练运用L一法则求未定式的极限 ③掌握函数展开成Taylor公式的方法,熟记 e*,sinx,cosx,In(1+x),(1+x) 的Taylor公式
难点 中值定理 L, Hospital法则的运用 利用中值定理证明不等式 基本要求 ①正确理解和掌握R、L、C、T定理及它们之 间的关系 ②熟练运用L—法则求未定式的极限 ③掌握函数展开成Taylor公式的方法,熟记 e ,sin x,cos x,ln(1 x),(1 x) x + + 的Taylor公式