
第三节函数的极限 数列极限的定义 二、收敛数列的性质
第三节 函数的极限 一、数列极限的定义 二、收敛数列的性质

一、函数极限的定义 (一)自变量趋于有限值时函数的极限 定义.设函数f(x)在点x的某去心邻域内有定义 若V8>0,38>0,当0<x-<8时,有f(x)-A<8 则称常数A为函数f(x)当x→x,时的极限,记作 1imf(x)=A或f(x)→A(当x→xo) x→x0 即 1imf(x)=A三V8>0,38>0,当x∈U(xo,δ) x→x0 时,有f(x)-A<8
一、函数极限的定义 (一)自变量趋于有限值时函数的极限 定义 . 设函数 在点 的某去心邻域内有定义 , 0, 0, 当 0 x − x0 时, 有 f (x) − A 则称常数 A 为函数 当 时的极限, f x A x x = → lim ( ) 0 或 即 当 时, 有 若 记作
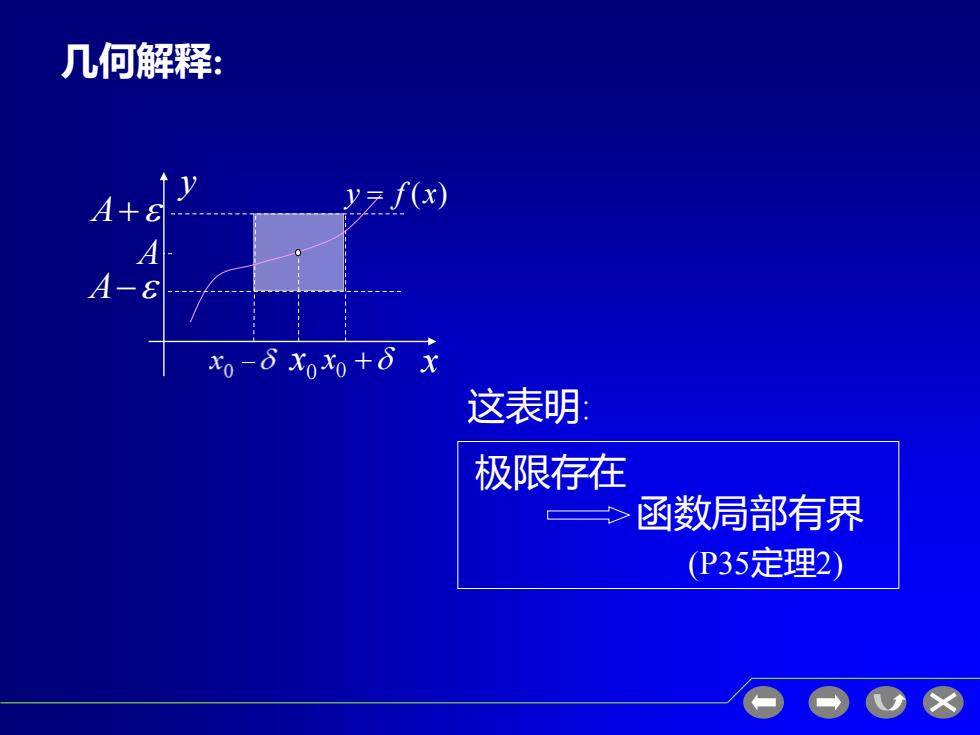
几何解释: A+8 f(x A A- x0-δX0x0+0x 这表明 极限存在 函数局部有界 (P35定理2)
几何解释: x0 + A+ A− A x0 x y y = f (x) 极限存在 函数局部有界 (P35定理2) 这表明:

例1、 证明 limC=C(C为常数) x→X0 证: |f(x)-A=C-C=0 故V8>0,对任意的δ>0,当0<x-x<8时, 总有 C-C=0<8 因此 lim C=C x->xo
例1、 证明 证: f (x) − A 故 0, 对任意的 0, 当 时 , 因此 总有

例2、 证明lim(2x-1)=1 x1 证: f(x)-A=(2x-1)-1=2x-1 V8>0欲使f()-A<c,只要x-1<2, 取8=2,则当0<x-1<8时,必有 f(x)-A=(2x-1)-1<6 因此 1im(2x-1)=1 x->1
例2、 证明 证: = 2 x −1 0, 欲使 取 , 2 = 则当 0 x −1 时 , 必有 因此 只要