
注意:(1)直线的曲率处处为零; (2)圆上各点处的曲率等于半径的倒数,且 半径越小曲率越大. 2.曲率的计算公式 设y=f(x)二阶可导,:tana=y, y” 有a=ar心stany,da=1中y, 凼=T+.k= 3 (1+y2)2
2.曲率的计算公式 注意: (1) 直线的曲率处处为零; (2) 圆上各点处的曲率等于半径的倒数,且 半径越小曲率越大. 设y = f (x)二阶可导, tan = y , , 1 2 dx y y d + = . (1 ) 2 3 2 y y k + = 有 = arctan y , 1 . 2 ds = + y dx
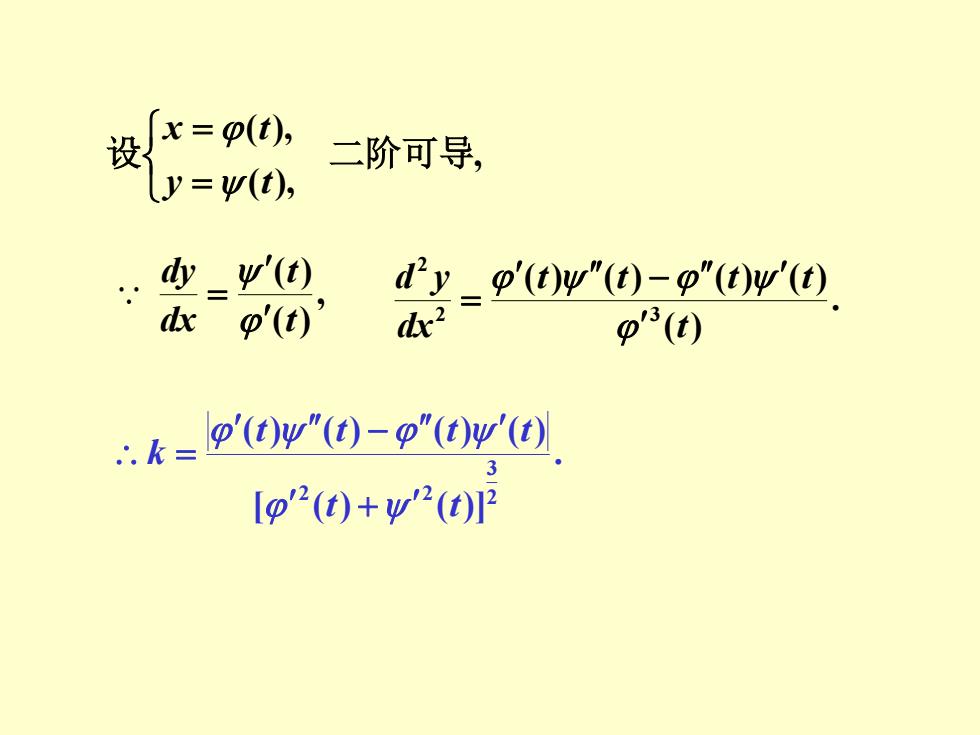
设 x=p(t), 二阶可导, (y=v(t), =V四 'y=p'y"()-p"(w'@ dx o'(t)' d21 p'3(t) k='w-p")w) [p2(t)+w'2(t)
, ( ), ( ), 设 二阶可导 = = y t x t . [ ( ) ( )] ( ) ( ) ( ) ( ) 2 3 2 2 t t t t t t k + − = , ( ) ( ) t t dx dy = . ( ) ( ) ( ) ( ) ( ) 2 3 2 t t t t t dx d y − =