
定积分的概念 前一章我们从导数的逆运算引出了不定积 分,系统地介绍了积分法,这是积分学的第一类 基本问题。本章先从实例出发,引出积分学的第 二类基本问题一定积分,它是微分(求局部量 )的逆运算(微分的无限求和一求总量),然 后着重介绍定积分的计算方法,它在科学技术领 域中有着极其广泛的应用。 重点 定积分的概念和性质,微积分基本公 式,定积分的换元法和分部积分法 难点 定义及换元法和分部法的运用
定积分的概念 前一章我们从导数的逆运算引出了不定积 分,系统地介绍了积分法,这是积分学的第一类 基本问题。本章先从实例出发,引出积分学的第 二类基本问题——定积分,它是微分(求局部量 )的逆运算(微分的无限求和——求总量),然 后着重介绍定积分的计算方法,它在科学技术领 域中有着极其广泛的应用。 重点 定积分的概念和性质,微积分基本公 式,定积分的换元法和分部积分法 难点 定义及换元法和分部法的运用

基车要求 ①正确理解定积分的概念及其实际背景 ②记住定积分的性质并能正确地运用 ③掌握变上限定积分概念,微积分基本定理, 并会用N-L公式计算定积分, ④能正确熟练地运用换元法和分部积分法 计算定积分 ⑤正确理解两类广义积分概念, 并会用定义计算一些较简单的广义积分
基本要求 ①正确理解定积分的概念及其实际背景 ②记住定积分的性质并能正确地运用 ③掌握变上限定积分概念,微积分基本定理, 并会用N-L公式计算定积分, ④能正确熟练地运用换元法和分部积分法 ⑤正确理解两类广义积分概念, 并会用定义 计算一些较简单的广义积分。 计 算定积分
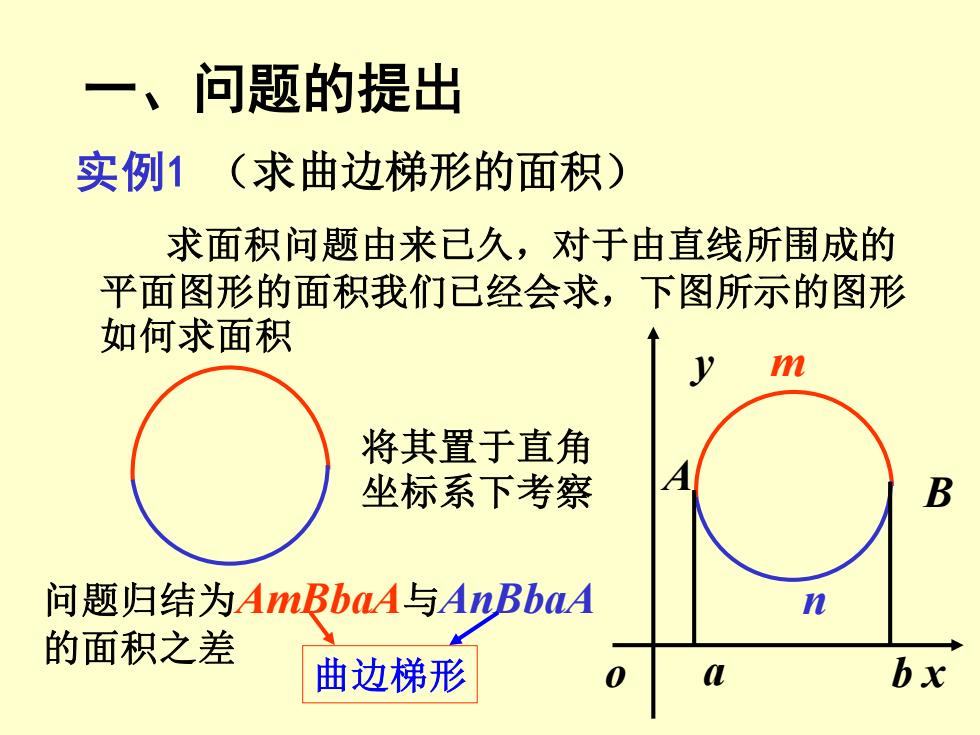
一、问题的提出 实例1(求曲边梯形的面积) 求面积问题由来已久,对于由直线所围成的 平面图形的面积我们己经会求,下图所示的图形 如何求面积 m 将其置于直角 坐标系下考察 B 问题归结为AmBbaA与AnBbaA n 的面积之差 曲边梯形 0 bx
实例1 (求曲边梯形的面积) 求面积问题由来已久,对于由直线所围成的 平面图形的面积我们已经会求,下图所示的图形 如何求面积 将其置于直角 坐标系下考察 o x y a b A B m 问题归结为AmBbaA与AnBbaA n 的面积之差 曲边梯形 一、问题的提出
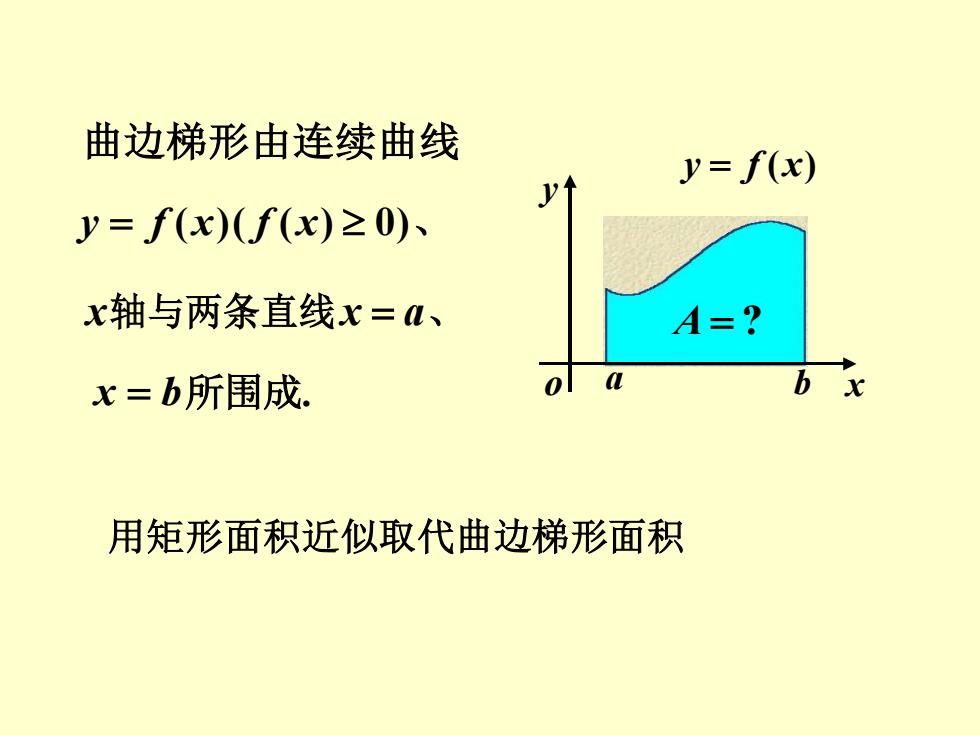
曲边梯形由连续曲线 y=f(x) 11 y=f(x)(f(x)≥0)、 x轴与两条直线x=M、 A=? x=b所围成. 用矩形面积近似取代曲边梯形面积
曲边梯形由连续曲线 y = f (x)( f (x) 0)、 x轴与两条直线x = a、 x = b所围成. a b x y o y = f (x) A = ? 用矩形面积近似取代曲边梯形面积
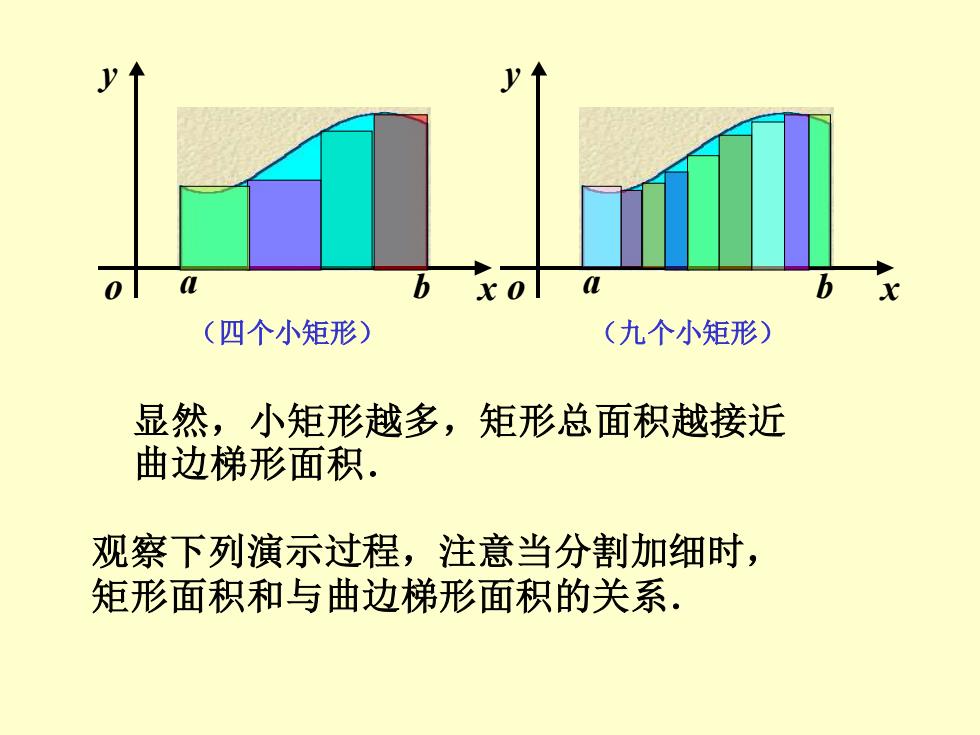
(四个小矩形) (九个小矩形) 显然,小矩形越多,矩形总面积越接近 曲边梯形面积. 观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系
a b x y o (四个小矩形) a b x y o (九个小矩形) 显然,小矩形越多,矩形总面积越接近 曲边梯形面积. 观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系.