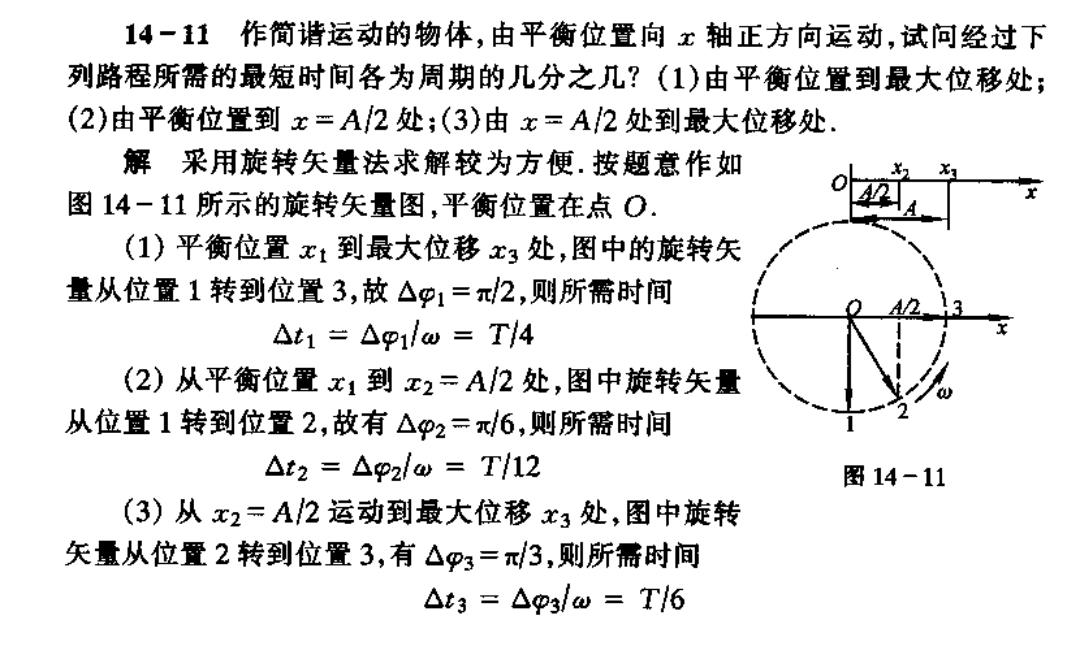
14一11作简谐运动的物体,由平衡位置向x轴正方向运动,试问经过下 列路程所需的最短时间各为周期的几分之几?(1)由平衡位置到最大位移处; (2)由平衡位置到x=A2处:(3)由x=A/2处到最大位移处, 解采用旋转矢量法求解较为方便.按题意作如 图14-11所示的旋转矢量图,平衡位置在点0. (1)平衡位置x1到最大位移x3处,图中的旋转矢 量从位置1转到位置3,故△g1=π2,则所需时间 △t1兰△p1/w=T4 (2)从平衡位置x1到x2=A/2处,图中旋转矢量 从位置1转到位置2,故有△p2=6,则所需时间 △t2=△p2/w=T/12 图14-11 (3)从x2=A/2运动到最大位移x3处,图中旋转 矢量从位置2转到位置3,有△3=3,则所需时间 △t3=△p3/w=T6

14-12在一块平板下装有弹簧,平板上放一质量为1.0kg的重物.现使 平板沿竖直方向作上下简谐运动,周期为 0.50s,振幅为2.0×10-2m.求:(1)平板到 最低点时,重物对平板的作用力;(2)若频率 不变,则平板以多大的振幅振动时,重物会 跳离平板?(3)若振幅不变,则平板以多大 的频率振动时,重物会跳离平板? 分析按题意作示意图14-12.物体 77777元 在平衡位置附近随板作简谐运动,其间受重 力P和板支持力FN作用,FN是一个变力 按牛顿定律,有 图14-12 F =mg FN m dt (1) 由于物体是随板一起作简谐运动,因而有a=正之=一Awcs(ad+p),贴 式(1)可改写为 FN=mg mAwzcos(at +o) (2) (1)根据板运动的位置,确定此刻振动的相位+P,由式(2)可求板与物 体之间的作用力. (2)由式(2)可知支持力FN的值与振幅A、角频率w和相位(+P)有 关,在振动过程中,当+P=π时FN最小.而重物恰好跳离平板的条件为FN =0,因此由式(2)可分别求出重物跳离平板所需的频率或振幅。 解(1)由分析可知,重物在最低点时,相位+=D,物体受板的支持力 FN mg mAw2 mg mA(2n/T)2 12.96N 重物对木块的作用力与FN大小相等,方向相反 (2)当频率不变时,设振幅变为A'.根据分析中所述,将FN=0及此+中二 π代入分析中式(2),可得 A'=mg ma2=gT214x2=6.2×10-2n (3)当振幅不变时,设频率变为v'.同样将FN=0及t+P=π代人分析中 式(2),可得 =元=盆mg=3.52b