
14-6为了测得一物体的质量,将其挂到一弹笺上,并让其自由振动 测得振动频率1=1.0Hz;若再将另一个质量m'=0.5kg的物体单独挂在该 弹簧上时,测得振动频率y2=2.0Hz.设振动均在弹簧弹性限度内进行,求被测 物体的质量. 分折物体挂在弹簧上组成弹簧振子系统,其振动频率y=m,即 c√1m.采用比较频率y的方法可求出未知物体的质量. 解由分析可知v心√1m,则有y/2=√mTm.根据题中给出的数据可 得物体的质量为 m=m'(zl1)2=2.0kg

14-7在如图14-7(a)所示装置中,一动度系数为k的轻弹簧,一端固定 在墙上,另一端连按一质量为m1的物体A,置于光滑水平桌面上.现通过一质 量m、半径为R的定滑轮B(可视为匀质圆盘)用细绳连接另一质量为m2的物 体C.设细绳不可伸长,且与滑轮间无相对滑动,求系统的振动角期率, ww 777777777 (a) (b) 中c e) 图14-7 分析这是一个由弹簧、物体A、C和滑轮B组成的简谐运动系统.求解系 统的振动频率可采用两种方法,(1)从受力分析着手.如图14-7(b)所示,设系 统处于平衡状态时,与物体A相连的弹簧一端所在位置为坐标原点O,此时弹 簧已伸长x0,且缸0=m2g.当弹簧沿Ox轴正向从原点O伸长x时,分析物体 A,C及滑轮B的受力情况,并分别列出它们的动力学方程,可解得系统作简谐 运动的微分方程.(2)从系统机械能守恒着手.列出系统机械能守恒方程,然后求 得系统作简请运动的微分方程。 解1在图14-7(b)的状态下,各物体受力如图14-7(c)所示.其中F= -(x+x0)t.考惠到绳子不可伸长,对物体A、B、C分别列方程,有 Fn-(x+x0)=m1dr2 (1) m2g-Fn m2 dii (2) (Fa~FnR=a=立mR (3) kxo m2g (4) 方程(3)中用到了Fn=FFn=F2J=mR22及a=a/R.联立式(1)~式 (4)可得 d"x 十 dt2 n1+m2+m2工=0 (5) 则系统振动的角频率为 =√(m1+m2+m2】 解2取整个振动装置和地球为研究系统,因没有外力和非保守内力作功, 系统机械能守恒,设物体平衡时为初始状态,物体向右偏移距离x(此时速度为 口、加速度为α)为末状态,则由机械能守缸定律,有 受6=-m3肛+2m1u2+之m22+四2+(红+xo2 在列出上述方程时应注意势能(重力势能和弹性势能)零点的选取.为运算方便, 选初始状态下物体C所在位置为重力势能零点:弹簧原长时为弹性势能的零 点.将上述方程对时间求导得 0=-m0+m心0+m0+船+(红+)能 将J=mR22、R=v、duldt=fx/dt2和m2g=kru代人上式,可得 x m1+m2+m2x=0 (6) 式(6)与式(5)相同,表明两种解法结果一致

14-8一放置在水平桌面上的弹黄振子,振幅A=2.0×10-2m,周期T =0.50s.当t=0时,(1)物体在正方向端点:(2)物体在平衡位置、向负方向运 动:(3)物体在x=1.0×102m处,向负方向运动;(4)物体在x= -1.0×10-2m处,向正方向运动.求以上各种情况的运动方程. 分析在鞭幅A和周期T已知的条件下,确定初相9是求解简谐运动方 程的关键.初相的确定通带有两种方法.(1)解析法:由振动方程出发,根据初始 条件,即t=0时,x=x0和v=%来确定g值.(2)旋转矢量法:如图14-8(a) 所示,将质点P在Ox轴上振动的韧始位置x0和速度的方向与旋转矢最图 相对应来确定.旋转矢量祛比较直观、方便,在分析中常采用 () (b) 图14-8 解由题给条件知A=2.0×102m,w=2T=4xs',而初相伞可采用 分析中的两种不同方法来求。 解析法:根据简谐运动方程x=Acs(a+p),当t-0时有x0=AcsP, e0=-Awsin单.当 (1)x0=A时,0081=1,则1=0: (2)x0=0时,cs=0,p=±2,因0<0,取%=受: (3)x=1.0×102m时,c089=0.5,93=土弩.由0<0,取9=3: (4)0=-1.0×102m时,608p4=-0.5,P4=r±号,由0>0,取4- 43. 旋转矢量法:分别断出四个不同初始状态的旋转矢量图,如图14-8(b)所 示,它们所对应的初相分别为1=0,2=2,=3,p4=43 振幅A、角频率、初相单均确定后,则各相应状态下的运动方程为 (1)x=(2.0×10-2m)cos(4πs1)t (2)x=(2.0×102m)eo[(4xs1)t+/2] (3)x=(2.0×10-2m)c0s(4r8l)t+/3] (4)x=(2.0×10-2m)co8[(4xs1)t+4/3]
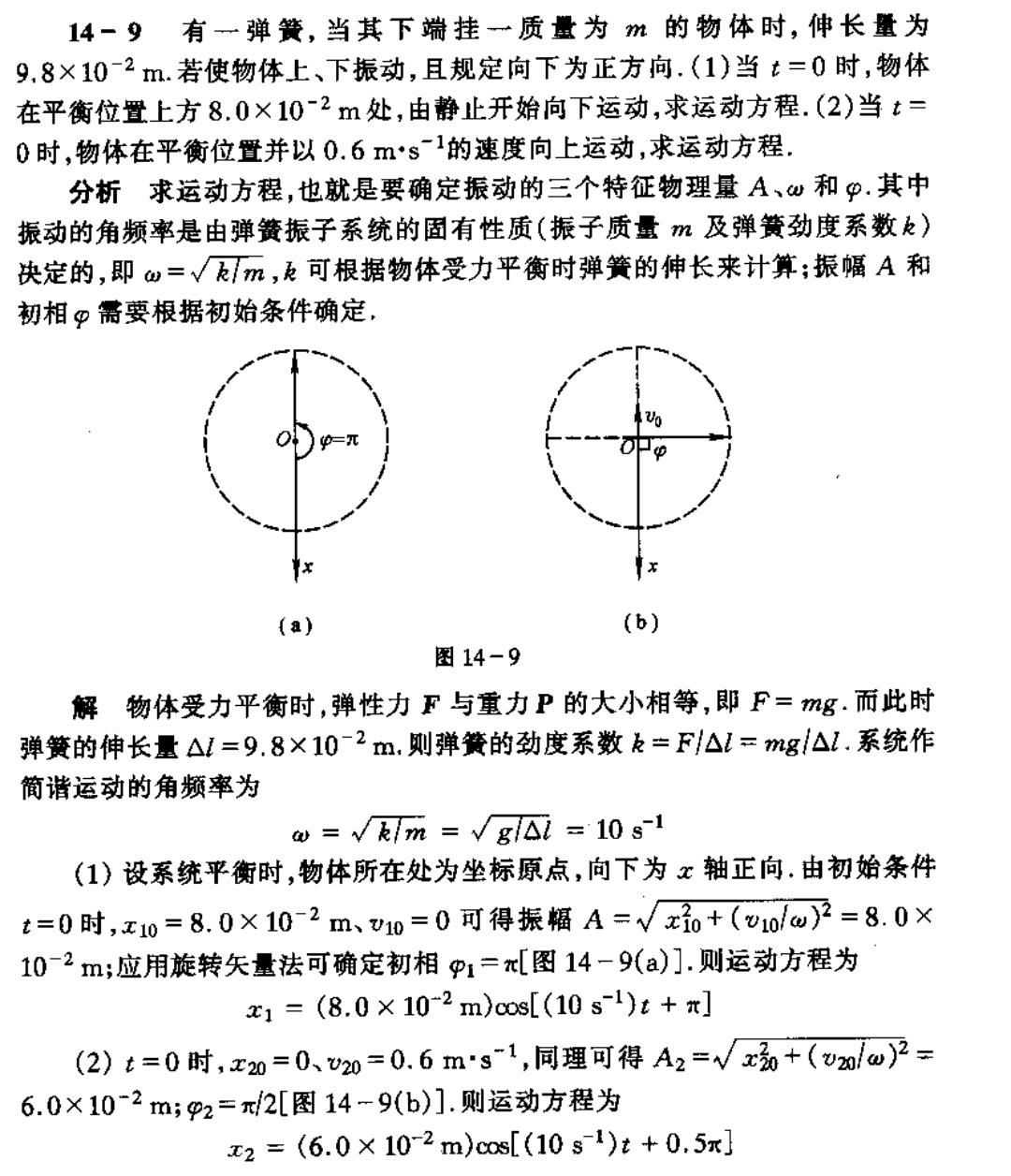
14一9有一弹簧,当其下端挂一质量为m的物体时,伸长量为 9,8×102m.若使物体上、下振动,且规定向下为正方向.(1)当t=0时,物体 在平衡位置上方8.0×10~2m处,由静止开始向下运动,求运动方程.(2)当:= 0时,物体在平衡位置并以0.6ms1的速度向上运动,求运动方程. 分析求运动方程,也就是要确定振动的三个特征物理量A、仙和的.其中 振动的角频率是由弹簧振子系统的固有性质(振子质量m及弹簧劲度系数k) 决定的,即仙=√m,可根据物体受力平衡时弹簧的神长来计算:振幅A和 韧相g需要根据初始条件确定 (a) (b) 图14-9 解物体受力平衡时,弹性力F与重力P的大小相等,即F=mg.而此时 弹簧的伸长量△1=9,8×10-2m.则弹簧的劲度系数k=F到△l=mg/△1.系统作 简著运动的角频率为 e=√km=√g01=10s1 (1)设系统平衡时,物体所在处为坐标原点,向下为x轴正向.由初始条件 t=0时,x10=8.0×102m、v10=0可得振幅A=√xi0+(v10/w=8.0× 102m;应用旋转矢量法可确定初相1=x[图14-9(a)].则运动方程为 x1=(8.0×10-2m)cos[(10s1)t+T] (2)t=0时,xn=0、0=0.6ms1,同理可得A2=√x0+(mw)2= 6.0×10-2m;2=2[图14-9(b)].则运动方程为 x2=(6.0×102m)cos[(10sl)t+0.5x]
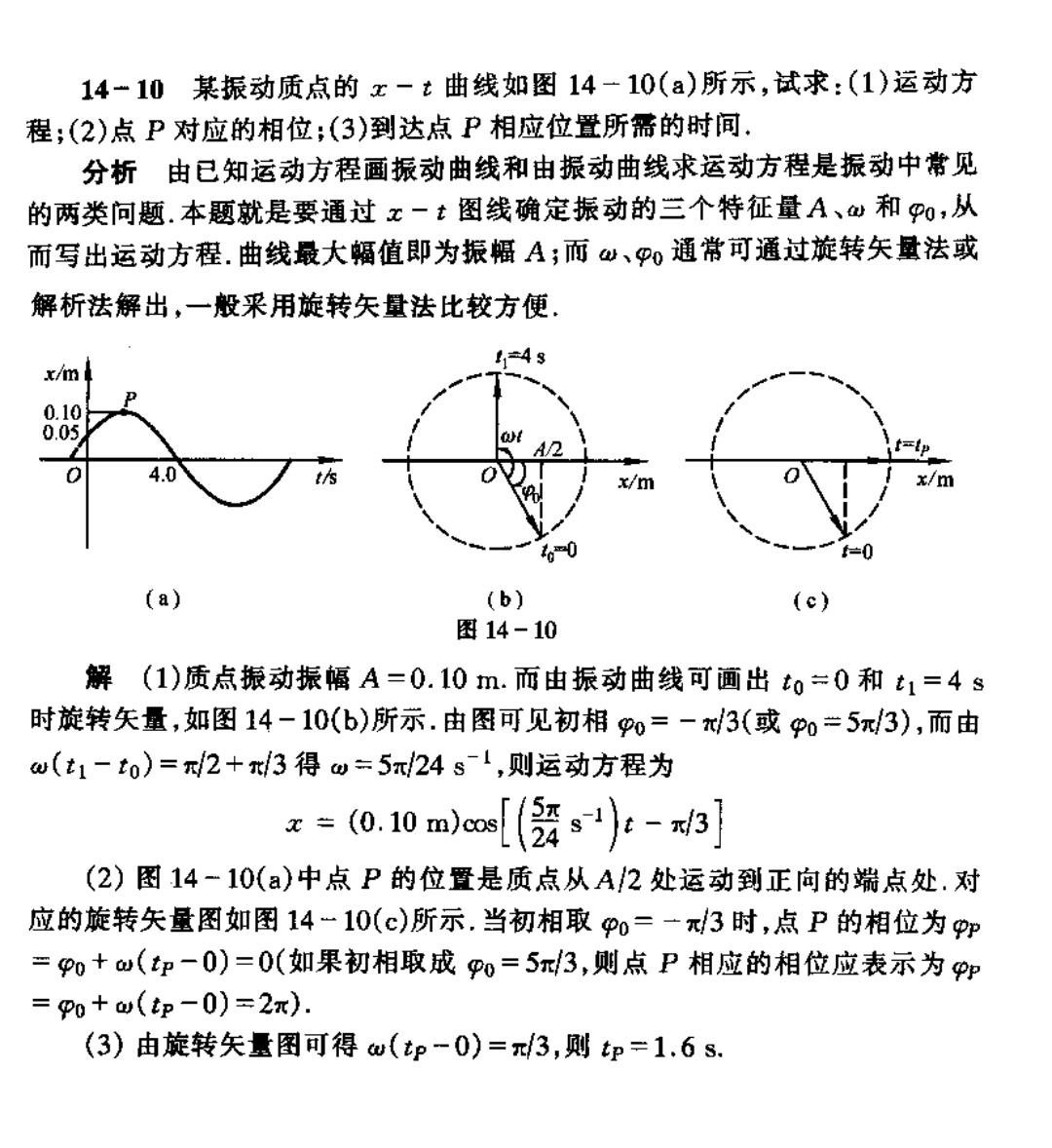
14-10某振动质点的x-t曲线如图14-10(a)所示,试求:(1)运动方 程;(2)点P对应的相位:(3)到达点P相应位置所需的时间. 分析由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见 的两类问题.本题就是要通过x一t图线确定振动的三个特征量A、仙和0,从 而写出运动方程.曲线最大幅值即为振幅A;而仙、P0通常可通过旋转矢量法或 解析法解出,一般采用旋转矢量法比较方便。 897 4.0 (a) (b) (c) 图14-10 解(1)质点振动振幅A=0.10m.而由振动曲线可画出t0=0和t1=4s 时旋转矢量,如图14-10(6)所示.由图可见初相0=-/3(或0=5π/3),而由 w(t1-to)=π2+/3得w=5π/24s1,则运动方程为 x=0.10ms[(赞s-3 (2)图14-10()中点P的位置是质点从A/2处运动到正向的端点处.对 应的旋转失量图如图14-10(c)所示.当初相取p0=一3时,点P的相位为 =p0+u(t印一0)=0(如果初相取成o=5π3,则点P相应的相位应表示为 =p0+u(p-0)=2x). (3)由旋转矢量图可得w(p-0)=π/3,则切=1.6s