
第四章根轨迹法 在时域分析法中己知控制系统的闭环特征根决定该控制系统的性能。那么,是 否对于每一个控制系统都必须求出其闭环特征根,才能够了解其性能呢?如果答案 是背定的,那么当特征多项式是三阶及以上时,求解特征根是一项比较复杂的工作。 特别是要分析系统特征式中某一参数(比如K)变化时对系统性能的影响,这种准 确求解每一个特征根的工作将会变得十分困难。 W.R.Evans提出了一种描述特征方程中某一参数与该方程特征根之间对应关系 的图解法,比较方便的解决了上述问题。这种方法就是本章要介绍的根轨迹法。 4.1根轨迹的基本概念 1.根轨迹的定义 系统参数(如开环增益K)由0→∞变化时,闭环特征根在s平面移动的轨迹 称为该系统的闭环根轨迹。 [例4单位反馈控制系统如图,绘制K变化时,系统极点的变化情况。 R,⑧ K☐Cs) s0.5s+1 C(s) 2K* R6g2+25+2K 特征方程 D(s)=s2+25+2K°=0 特征根 52=-1±V-2K 讨论当K=0时, 31=0,32=-2 K=0.5时,31=52=-1 K=1时, 52=-1±1 K→o时,2=-1土j0,绘出特征根的变化轨迹如图 0
41 第四章 根轨迹法 在时域分析法中已知控制系统的闭环特征根决定该控制系统的性能。那么,是 否对于每一个控制系统都必须求出其闭环特征根,才能够了解其性能呢?如果答案 是肯定的,那么当特征多项式是三阶及以上时,求解特征根是一项比较复杂的工作。 特别是要分析系统特征式中某一参数(比如 K*)变化时对系统性能的影响,这种准 确求解每一个特征根的工作将会变得十分困难。 W.R.Evans 提出了一种描述特征方程中某一参数与该方程特征根之间对应关系 的图解法,比较方便的解决了上述问题。这种方法就是本章要介绍的根轨迹法。 4.1 根轨迹的基本概念 1.根轨迹的定义 系统参数(如开环增益 K )由 0→∞变化时,闭环特征根在 s 平面移动的轨迹 称为该系统的闭环根轨迹。 [例 4-1] 单位反馈控制系统如图,绘制 K*变化时,系统极点的变化情况。 2 * * 2 2 2 ( ) ( ) s s K K R s C s + + = 特征方程 ( ) 2 2 0 2 * D s = s + s + K = 特征根 * s1,2 = −1 1− 2K 讨论 当 0 * K = 时, s1 = 0 , s2 = −2 0.5 * K = 时, s1 = s2 = −1 1 * K = 时, s1,2 = −1 j1 → * K 时, s1,2 = −1 j ,绘出特征根的变化轨迹如图 jω × × s(0.5s 1) K + R(s) C(s) -2 -1 0

显然,当0<K<0.5时,系统取得二不相等实数根(过阻尼): K=0.5时,系统取得二相等实数根(临界阻尼): K·>0.5时,系统取得一对共轭复数根(欠阻尼)。 越大,共轭复数根离对称轴(实轴)越远. 指定一个K'值,就可以在根轨迹上找到对应的二个特征根,指定根轨迹上任意 一特征根的位置,就可以求出该特征根对应的K值和其余特征根。下面我们讨论根 轨迹的一般情况 2.根轨迹方程及幅值条件、相角条件 既然根轨迹是闭环特征根随参数变化的轨迹,则描述其变化关系的闭环特征方 程就是根轨迹方程。 设系统开环传递函数为 K'I(s-=) G(s)H(s)= (4-1) [I-p) 其中,K称为根轨迹增益:二,是开环零点:P,是开环极点。 则根轨迹方程(系统闭环特征方程)为 1+G(s)H(s)=0 K'II(s-=) 即 -1 (4-2) Πs-p,) 显然,满足上式的s即是系统的闭环特征根。 当K`从0变化到∞时,n个特征根将随之变化出n条轨迹。这n条轨迹就是系 统的闭环根轨迹(简称根轨迹)。 由式(4-2)确定的根轨迹方程可以分解成相角条件和幅值条件 三4+24+p)-空0-2a,=±2k+r (4-3)
42 显然,当 0 0.5 * K 时,系统取得二不相等实数根(过阻尼); 0.5 * K = 时,系统取得二相等实数根(临界阻尼); 0.5 * K 时,系统取得一对共轭复数根(欠阻尼)。 * K 越大,共轭复数根离对称轴(实轴)越远. 指定一个 * K 值,就可以在根轨迹上找到对应的二个特征根,指定根轨迹上任意 一特征根的位置,就可以求出该特征根对应的 * K 值和其余特征根。下面我们讨论根 轨迹的一般情况。 2.根轨迹方程及幅值条件、相角条件 既然根轨迹是闭环特征根随参数变化的轨迹,则描述其变化关系的闭环特征方 程就是根轨迹方程。 设系统开环传递函数为 = = − − = n j i m i i s p K s z G s H s 1 1 * ( ) ( ) ( ) ( ) (4-1) 其中, * K 称为根轨迹增益; i z 是开环零点; j p 是开环极点。 则根轨迹方程(系统闭环特征方程)为 1+ G(s)H(s) = 0 即 1 ( ) ( ) 1 1 * = − − − = = n j j m i i s p K s z (4-2) 显然,满足上式的 s 即是系统的闭环特征根。 当 * K 从 0 变化到∞时,n 个特征根将随之变化出 n 条轨迹。这 n 条轨迹就是系 统的闭环根轨迹(简称根轨迹)。 由式(4-2)确定的根轨迹方程可以分解成相角条件和幅值条件 ( ) ( ) (2 1) 1 1 1 1 + − + = − = + = = = = s z s p k m i n l i l m i n l i l (4-3)

K'IIls-=l (44) -p叭 几点说明: 1.开环零点、极点p是决定闭环根轨迹的条件。 2.注意到式(4-3)定义的相角条件不含有K,它表明满足式(44)的任意K值均满 足由相角条件定义的根轨迹,因此,相角条件是决定闭环根轨迹的充分必要条件。 3.满足相角条件的闭环极点s值,代入幅值条件式(44),就可以求出对应的K值, 显然一个K'对应个3值,满足幅值条件的s值不一定满足相角条件。因此由幅值 条件(及其变化式)求出的5值不一定是根轨迹上的根。 任意特征方程D(s)=0均可处理成1+G(s)H(s)=0的形式,其中把 G(s)H(s)写成式(4-4)描述的形式就可以得到K`值,所以说K可以是系统任意参 数。以其它参数为自变量作出的根轨迹称广义根轨迹。 4.2绘制根轨迹的基本规则 规则1根轨迹的对称性:相对于实轴对称 规则2根轨迹的分支数及其起点和终点: 根轨迹的分支数为n个:根轨迹起始于开环极点,终止于开环零点(包括无限 远零点)。 规则3根轨迹在实轴上的分布 实轴上有根轨迹的区段为右侧的开环实极点与开环实零点数目之和为奇数。 规则4根轨迹的渐近线:(当n-m≥2时) 与实轴交点坐标 -0,岛 (4-5) 与实轴正方向的夹角 0=于2k+1z (4-6) n-m 式中k依次取01,2一直到获得(n-m)个倾角为止。 规则5根轨迹的分离点(或汇合点):
43 1 1 1 * = − − = = n j j m i i s p K s z (4-4) 几点说明: 1. 开环零点 zi、极点 pj 是决定闭环根轨迹的条件。 2.注意到式(4-3)定义的相角条件不含有 * K ,它表明满足式(4-4)的任意 * K 值均满 足由相角条件定义的根轨迹,因此,相角条件是决定闭环根轨迹的充分必要条件。 3.满足相角条件的闭环极点 s 值,代入幅值条件式(4-4),就可以求出对应的 * K 值, 显然一个 * K 对应 n 个 s 值,满足幅值条件的 s 值不一定满足相角条件。因此由幅值 条件(及其变化式)求出的 s 值不一定是根轨迹上的根。 任意特征方程 D(s) = 0 均可处理成 1+ G(s)H(s) = 0 的形式,其中把 G(s)H(s) 写成式(4-4)描述的形式就可以得到 * K 值,所以说 * K 可以是系统任意参 数。以其它参数为自变量作出的根轨迹称广义根轨迹。 4.2 绘制根轨迹的基本规则 规则 1 根轨迹的对称性:相对于实轴对称; 规则 2 根轨迹的分支数及其起点和终点: 根轨迹的分支数为 n 个;根轨迹起始于开环极点,终止于开环零点(包括无限 远零点)。 规则 3 根轨迹在实轴上的分布 实轴上有根轨迹的区段为右侧的开环实极点与开环实零点数目之和为奇数。 规则 4 根轨迹的渐近线:(当 n − m 2 时) 与实轴交点坐标 n m p z m i i n l l A − − − − − = =1 =1 ( ) ( ) (4-5) 与实轴正方向的夹角 ( ) n m k − + = 2 1 (4-6) 式中 k 依次取 0,1,2 一直到获得( n − m )个倾角为止。 规则 5 根轨迹的分离点(或汇合点):

(1)不是所有的系统在绘制根轨迹时,都要求分离点(或汇合点):只有当两 个开环极点之间有根轨迹时,才存在分离点:当两个开环零点(包括一个无限零点) 之间有根轨迹时,则存在汇合点:当一个开环极点和一个开环零点(可以是无限零 点)之间有根轨迹时,一般没有分离点,若有,则必然是成对出现的。 (2)根轨迹的分离点(或汇合点)的求取: 若令系统的开环传递函数为:G6H)=K,B A(s) 则 dK=0,或 ds A(s)B'(s)-A(s)B(s)=0 (47) 根轨迹的分离点(或汇合点)是A(s)B'(s)-A(s)B(s)=0的根, (3)满足As)B'(s)-A"(s)B(s)=0的根不一定都是根轨迹的分离点(或汇合 点),分离点(或汇合点)必须在根轨迹上:如果有的根不在根轨迹上,则应该舍去。 规则6根轨迹与虚轴的交点 (1)当根轨迹可能和虚轴相交时,需要求根轨迹与虚轴的交点:否则,无需求 取。 (2)根轨迹与虚轴的交点的求取: ①由劳斯判据可求得交点的坐标及相应的K。值: ②在特征方程中,令5=0,然后使特征方程的实部和虚部分别为零,可求得交点 的坐标及相应的K。=K,值。 ③根轨迹和虚轴交点处相当于系统处于临界稳定状态。此时增益K,称为临界根轨迹 增益。 规则7根轨迹的出射角和入射角 系统中存在开环共轭复极点(或复零点)时,需要求出射角和入射角。 出射角: 0,=2k+1)z+∑0,-∑0 (4-8) 入射角: 9=2k+r+20,-20 (49) 典型开环极点、零点分部及其相应的根轨迹如表4-1所示
44 (1)不是所有的系统在绘制根轨迹时,都要求分离点(或汇合点);只有当两 个开环极点之间有根轨迹时,才存在分离点;当两个开环零点(包括一个无限零点) 之间有根轨迹时,则存在汇合点;当一个开环极点和一个开环零点(可以是无限零 点)之间有根轨迹时,一般没有分离点,若有,则必然是成对出现的。 (2)根轨迹的分离点(或汇合点)的求取: 若令系统的开环传递函数为: ( ) ( ) ( ) ( ) 0 A s K B s G s H s = 则 0 0 = ds dK ,或 A(s)B(s) − A(s)B(s) = 0 (4-7) 根轨迹的分离点(或汇合点)是 A(s)B(s) − A(s)B(s) = 0 的根, (3)满足 A(s)B(s) − A(s)B(s) = 0 的根不一定都是根轨迹的分离点(或汇合 点),分离点(或汇合点)必须在根轨迹上;如果有的根不在根轨迹上,则应该舍去。 规则 6 根轨迹与虚轴的交点 (1)当根轨迹可能和虚轴相交时,需要求根轨迹与虚轴的交点;否则,无需求 取。 (2)根轨迹与虚轴的交点的求取: ①由劳斯判据可求得交点的坐标及相应的 K0 值; ②在特征方程中,令 s = j ,然后使特征方程的实部和虚部分别为零,可求得交点 的坐标及相应的 K0 = Kl 值。 ③根轨迹和虚轴交点处相当于系统处于临界稳定状态。此时增益 Kl 称为临界根轨迹 增益。 规则 7 根轨迹的出射角和入射角 系统中存在开环共轭复极点(或复零点)时,需要求出射角和入射角。 出射角: = = = + + − m i n j l j l i j k 1 1 (2 1) (4-8) 入射角: = = = + + − n j m i l i k j i k 1 1 (2 1) (4-9) 典型开环极点、零点分部及其相应的根轨迹如表 4-1 所示
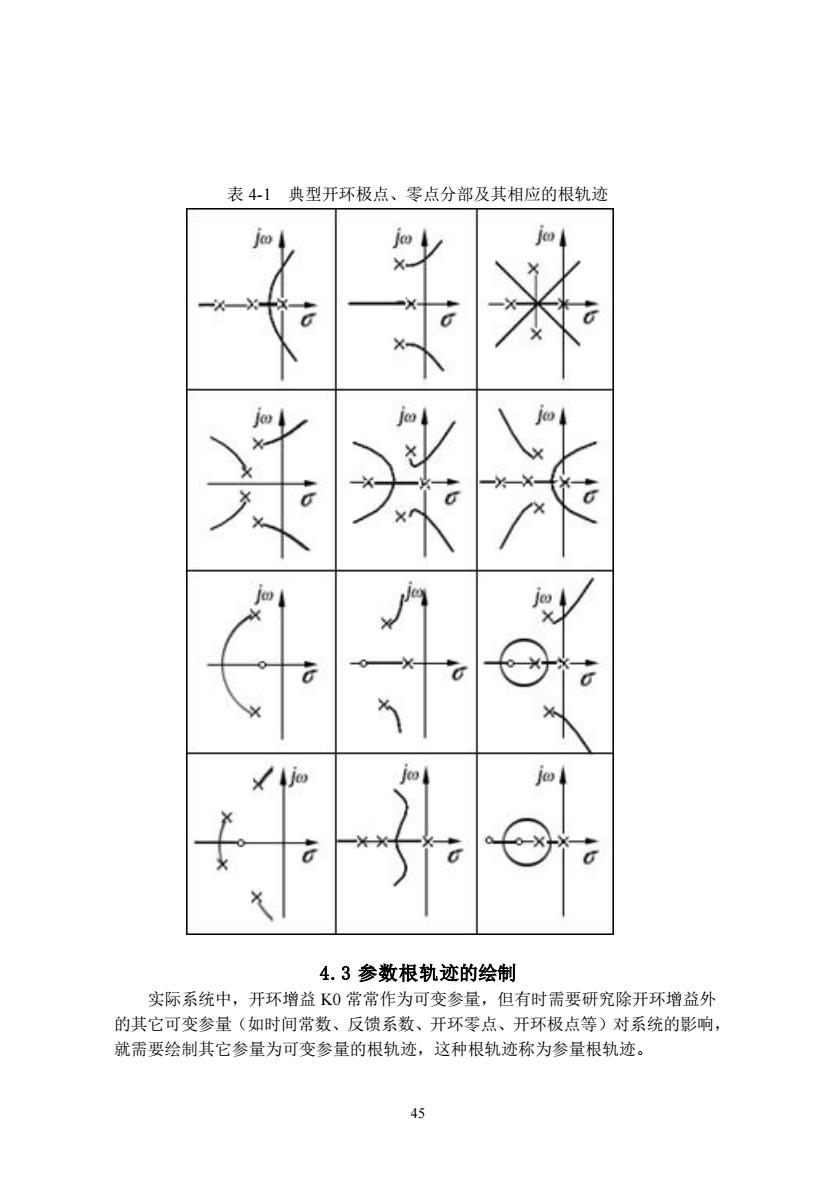
表41典型开环极点、零点分部及其相应的根轨迹 4.3参数根轨迹的绘制 实际系统中,开环增益K0常常作为可变参量,但有时需要研究除开环增益外 的其它可变参量(如时间常数、反馈系数、开环零点、开环极点等)对系统的影响 就需要绘制其它参量为可变参量的根轨迹,这种根轨迹称为参量根轨迹
45 表 4-1 典型开环极点、零点分部及其相应的根轨迹 4.3 参数根轨迹的绘制 实际系统中,开环增益 K0 常常作为可变参量,但有时需要研究除开环增益外 的其它可变参量(如时间常数、反馈系数、开环零点、开环极点等)对系统的影响, 就需要绘制其它参量为可变参量的根轨迹,这种根轨迹称为参量根轨迹