
第五章频率响应法 用时域分析法分析和研究系统的动态特性和稳态误差最为直观和准确,但是, 用解析方法求解高阶系统的时域响应往往十分困难。此外,由于高阶系统的结构和 参数与系统动态性能之间没有明确的函数关系,因此不易看出系统参数变化对系统 动态性能的影响。当系统的动态性能不能满足生产上要求的性能指标时,很难提出 改善系统性能的途径。 本章介绍的频域分析法是研究控制系统的一种经典方法,是在频域内应用图解 分析法评价系统性能的一种工程方法。频率特性可以由微分方程或传递函数求得, 还可以用实验方法测定。频域分析法不必直接求解系统的微分方程,而是间接地揭 示系统的时域性能,它能方便的显示出系统参数对系统性能的影响,并可以进一步 指明如何设计校正。 5.1频率特性 (1)在正弦输入信号的作用下,系统输出的稳态分量与输入正弦信号的复数比 称为系统的频率特性。 (2)频率特性与传递函数的关系为: G(j)=G(s)=j 微分方程 频率特性、微分方程与传递函数三种数学模型 之间关系如图5-1所示 传递函 (3)频率特性的表示方法 GUj)=Gljoje=A(0e=P(@)+j) ,频率特性。 其中: A(@)=G(j@)=P(@)2+Q(@) 图51频率华 性 A(o)和p(o)分别表示幅频特性和相频特性 P(o)和Q()分别表示实频特性和虚频特性。 ①幅相领率特性 又称奈奎斯特图(guis,极坐标图。它是以为参变量,以复平面的矢量表 示G(jo的一种方法。G(Uo)的幅值为A(o),相角为p(o)(从正实轴开始,逆 时针为正)。当频率0从0变化到∞时,GU)这个矢量的矢端在复平面上描绘出 的曲线就称为系统的幅相频率特性,可由A(o)和p(o)或P(@)和Q()来绘制。 ②对数颜率特性(又称伯德图,共两条曲线L(o)和()) 将幅频特性A(o)用增益L()来表示,其关系为:L()=20lgA(),称作对 60
60 第五章 频率响应法 用时域分析法分析和研究系统的动态特性和稳态误差最为直观和准确,但是, 用解析方法求解高阶系统的时域响应往往十分困难。此外,由于高阶系统的结构和 参数与系统动态性能之间没有明确的函数关系,因此不易看出系统参数变化对系统 动态性能的影响。当系统的动态性能不能满足生产上要求的性能指标时,很难提出 改善系统性能的途径。 本章介绍的频域分析法是研究控制系统的一种经典方法,是在频域内应用图解 分析法评价系统性能的一种工程方法。频率特性可以由微分方程或传递函数求得, 还可以用实验方法测定。频域分析法不必直接求解系统的微分方程,而是间接地揭 示系统的时域性能,它能方便的显示出系统参数对系统性能的影响,并可以进一步 指明如何设计校正。 5.1 频率特性 (1)在正弦输入信号的作用下,系统输出的稳态分量与输入正弦信号的复数比 称为系统的频率特性。 (2)频率特性与传递函数的关系为: s j G j G s = = ( ) ( ) 频率特性、微分方程与传递函数三种数学模型 之间关系如图 5-1 所示 (3)频率特性的表示方法 ( ( ) ( ) ( ) ( ) ( ) G j ) G(j )e A e P jQ j G j j = = = + 其中: 2 2 A() = G( j) = P() + Q() ( ) ( ) ( ) ( ) P Q = G j = arctg A() 和 () 分别表示幅频特性和相频特性, P() 和 Q() 分别表示实频特性和虚频特性。 ①幅相频率特性 又称奈奎斯特图 (Nyquist) ,极坐标图。它是以 为参变量,以复平面的矢量表 示 G( j ) 的一种方法。 G( j ) 的幅值为 A() ,相角为 () (从正实轴开始,逆 时针为正)。当频率 从 0 变化到∞时, G( j ) 这个矢量的矢端在复平面上描绘出 的曲线就称为系统的幅相频率特性,可由 A() 和 () 或 P() 和 Q() 来绘制。 ②对数频率特性(又称伯德图,共两条曲线 L() 和 () ) 将幅频特性 A() 用增益 L() 来表示,其关系为: L() = 20lg A() ,称作对 系统 频率特性 微分方程 传递函数 dt d s = dt d j = s = j 图 5-1 频率特性、微分方程与传递函数 三种数学模型之间关系

数幅频特性。其横坐标为o,常用对数go分度:纵坐标为L(o,单位为dB。对 数相频特性的横坐标与对数幅频特性相同,按对数刻度,标以频率值,纵坐标为 (),单位为度()。 对数幅频特性和对数相频特性合称为对数频率特性,或称作伯德图(Bod阳)。 5.2对数坐标图(Bode图) 5.2.1典型环节频率特性的伯德图 1.比例环节K) 比例环节的对数幅频特性和对数相频特性分别是 「L(o)=20gK p(o)=09 比例环节的伯德图如图5-1所示。 K2≥1 少-。 图5一1比例环节的伯德图 2.积分环节】 和微分环节(s) (s 积分环节的对数幅频特性和对数相频特性为 L(o)=20g 1 =20lg=-20lgo(dB) jo p(o)= 上=g0)=-90 1-1 积分环节比例环节的伯德图如图5-2所示。 61
61 数幅频特性。其横坐标为 ,常用对数 lg 分度;纵坐标为 L() ,单位为 dB 。对 数相频特性的横坐标与对数幅频特性相同,按对数刻度,标以频率ω值,纵坐标为 () ,单位为度(o)。 对数幅频特性和对数相频特性合称为对数频率特性,或称作伯德图 (Bode) 。 5.2 对数坐标图(Bode 图) 5.2.1 典型环节频率特性的伯德图 1.比例环节(K) 比例环节的对数幅频特性和对数相频特性分别是 = = 0 ( ) 0 ( ) 20lg L K 比例环节的伯德图如图 5-1 所示。 图 5—1 比例环节的伯德图 2.积分环节 s 1 和微分环节(s) 积分环节的对数幅频特性和对数相频特性为 = = − = − = − = = = − −1 0 / 0) 90 1 ( 1 1 ( ) 20lg ( ) 1 20lg 1 ( ) 20lg j tg j dB j L 积分环节比例环节的伯德图如图 5-2 所示
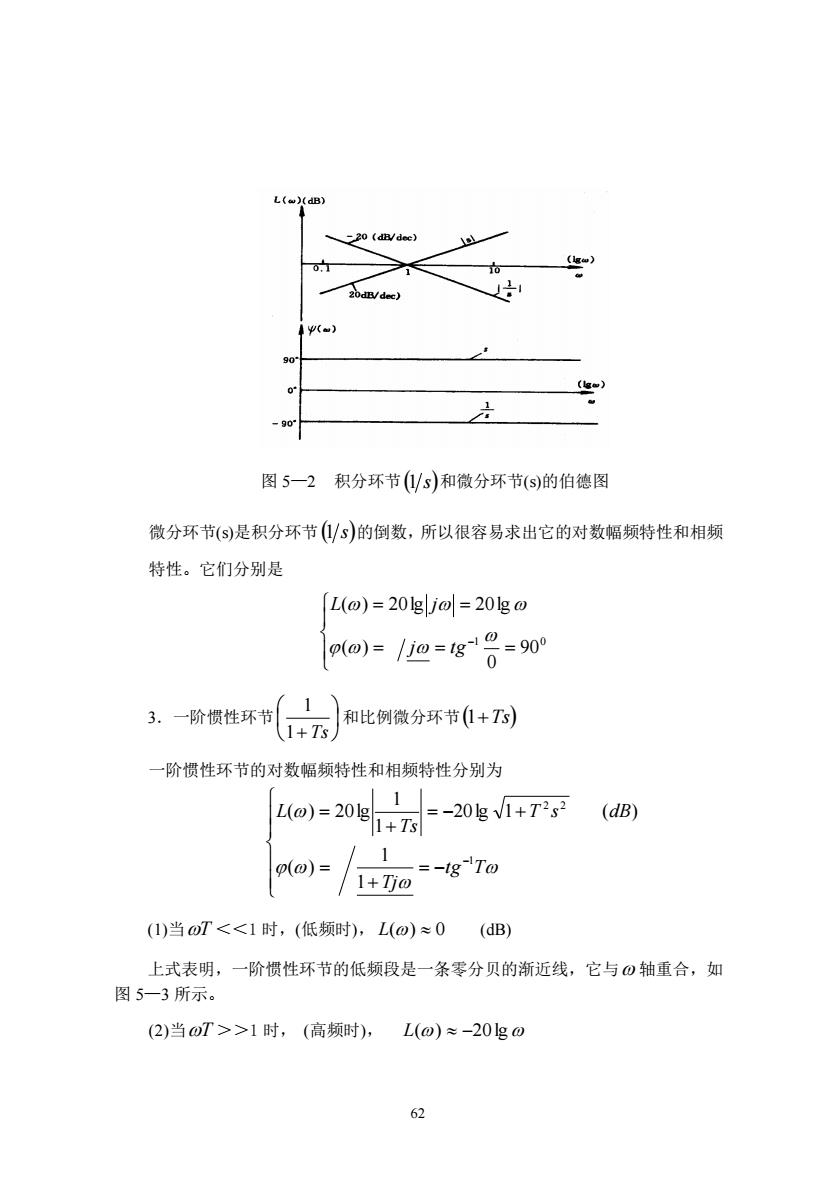
L(w)(dB 2v 图5一2积分环节(/s)和微分环节(s)的伯德图 微分环节(S)是积分环节(/S)的倒数,所以很容易求出它的对数幅频特性和相频 特性。它们分别是 [L(o)=20gja可l=20lgw 0(o)=/j0=g1e=900 0 3.一阶惯性环节1)】 和比例微分环节(1+TS) (1+Ts) 一阶惯性环节的对数幅频特性和相频特性分别为 4o)=20g|1 =-20g1+T2s2 (dB) 1+T /1 p(@)= /1+万0 =-Ig-To ()当oT<<1时,(低频时),L(o)≈0(dB) 上式表明,一阶惯性环节的低频段是一条零分贝的渐近线,它与0轴重合,如 图5一3所示。 (2)当oT>>1时,(高频时),L(@)≈-20g0 62
62 图 5—2 积分环节 (1 s) 和微分环节(s)的伯德图 微分环节(s)是积分环节 (1 s) 的倒数,所以很容易求出它的对数幅频特性和相频 特性。它们分别是 = = = = = −1 0 90 0 ( ) ( ) 20lg 20lg j tg L j 3.一阶惯性环节 1+ Ts 1 和比例微分环节 (1+Ts) 一阶惯性环节的对数幅频特性和相频特性分别为 = − + = = − + + = − tg T Tj T s dB Ts L 1 2 2 1 1 ( ) 20lg 1 ( ) 1 1 ( ) 20lg (1)当 T <<1 时,(低频时), L() 0 (dB) 上式表明,一阶惯性环节的低频段是一条零分贝的渐近线,它与 轴重合,如 图 5—3 所示。 (2)当 T >>1 时, (高频时), L() −20lg
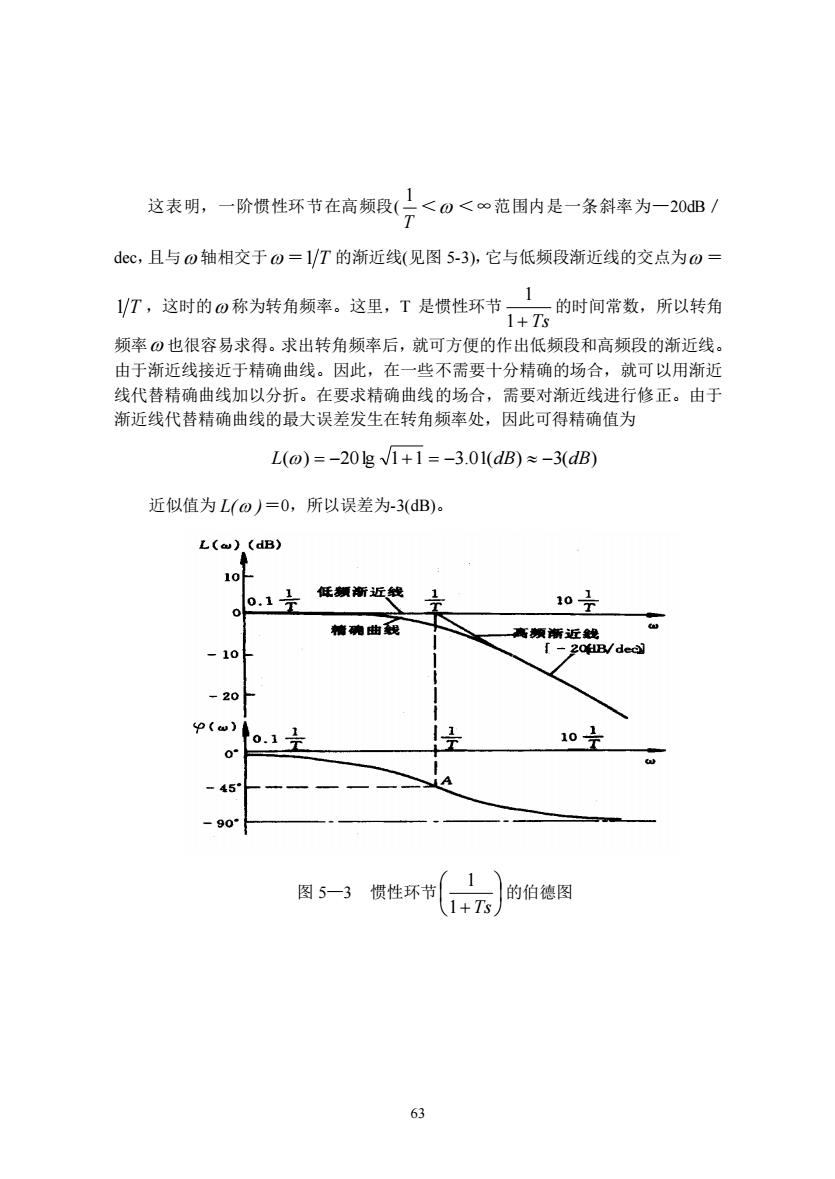
这表明,一阶惯性环节在高频段(行<0<∞范围内是一条斜率为一20dB/ de℃,且与o轴相交于0=1/T的渐近线(见图5-3),它与低频段渐近线的交点为0= VT,这时的0称为转角频率。这里,T是模性环节十元的时间宿数。所以转角 频率)也很容易求得。求出转角频率后,就可方便的作出低频段和高频段的渐近线。 由于渐近线接近于精确曲线。因此,在一些不需要十分精确的场合,就可以用渐近 线代替精确曲线加以分折。在要求精确曲线的场合,需要对渐近线进行修正。由于 渐近线代替精确曲线的最大误差发生在转角频率处,因此可得精确值为 L(o)=-20g√1+1=-3.01(dB)≈-3(dB) 近似值为L(o)=0,所以误差为-3(dB)。 L(o) (dB) 0.1÷ 低渐近 10子 精响曲我 -10 -20 w) o.1 10 -45 90 图5一3惯性环节 +的伯德图 63
63 这表明,一阶惯性环节在高频段( T 1 < <∞范围内是一条斜率为—20dB/ dec,且与 轴相交于 =1 T 的渐近线(见图 5-3),它与低频段渐近线的交点为 = 1 T ,这时的 称为转角频率。这里,T 是惯性环节 1+ Ts 1 的时间常数,所以转角 频率 也很容易求得。求出转角频率后,就可方便的作出低频段和高频段的渐近线。 由于渐近线接近于精确曲线。因此,在一些不需要十分精确的场合,就可以用渐近 线代替精确曲线加以分折。在要求精确曲线的场合,需要对渐近线进行修正。由于 渐近线代替精确曲线的最大误差发生在转角频率处,因此可得精确值为 L() = −20lg 1+1 = −3.01(dB) −3(dB) 近似值为 L( )=0,所以误差为-3(dB)。 图 5—3 惯性环节 1+ Ts 1 的伯德图
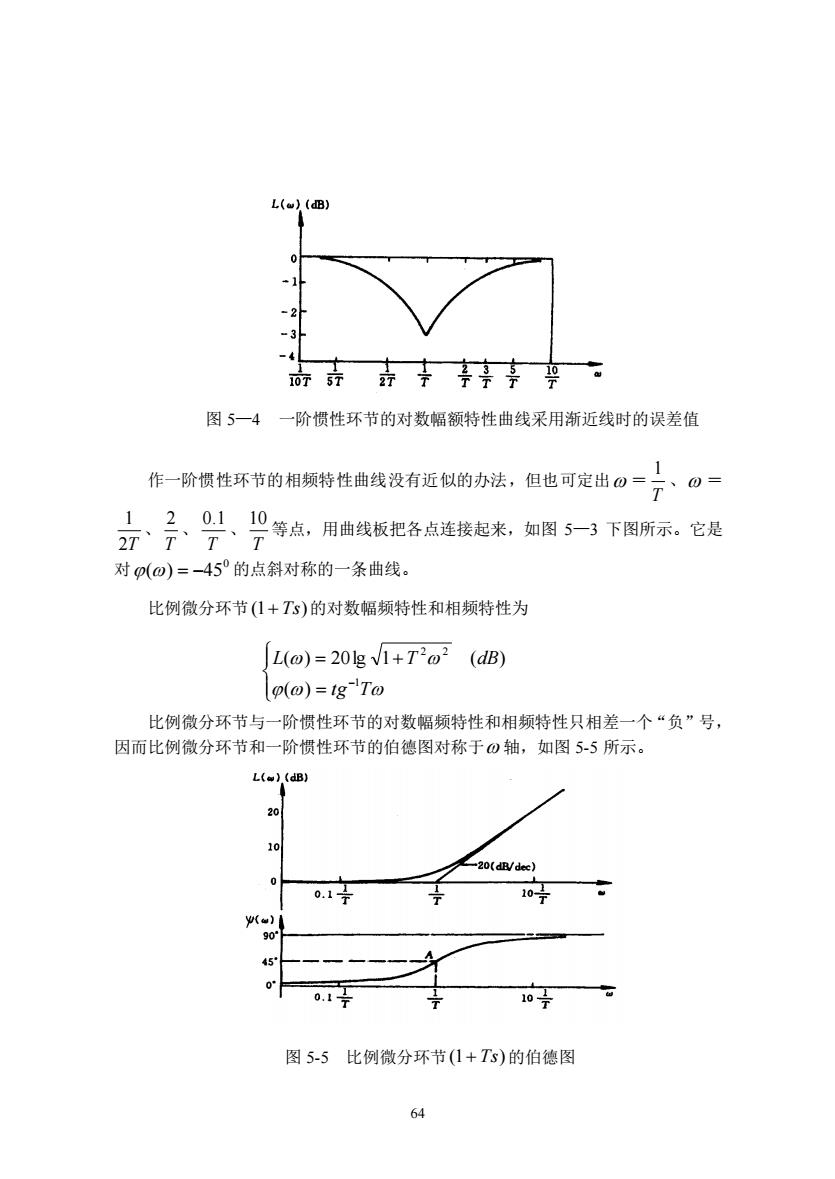
L()(dB -1 -3 赤寺去亭其亭华、 图5一4一阶惯性环节的对数幅额特性曲线采用渐近线时的误差值 作一阶模性环节的相频特性曲线设有近似的办法,但也可定出日=了、。 对p(o)=-45°的点斜对称的一条曲线。 比例微分环节(1+TS)的对数幅频特性和相频特性为 JL(@)=201g1+To2 (dB) o(o)=1g To 比例微分环节与一阶惯性环节的对数幅频特性和相频特性只相差一个“负”号, 因而比例微分环节和一阶惯性环节的伯德图对称于0轴,如图55所示。 L(),(dB) 20(d/de 0.17 10 45 0.1字 107 图5-5比例微分环节(1+Ts)的伯德图
64 图 5—4 一阶惯性环节的对数幅额特性曲线采用渐近线时的误差值 作一阶惯性环节的相频特性曲线没有近似的办法,但也可定出 = T 1 、 = 2T 1 、 T 2 、 T 0.1 、 T 10 等点,用曲线板把各点连接起来,如图 5—3 下图所示。它是 对 0 () = −45 的点斜对称的一条曲线。 比例微分环节 (1+ Ts) 的对数幅频特性和相频特性为 = = + − tg T L T dB 1 2 2 ( ) ( ) 20lg 1 ( ) 比例微分环节与一阶惯性环节的对数幅频特性和相频特性只相差一个“负”号, 因而比例微分环节和一阶惯性环节的伯德图对称于 轴,如图 5-5 所示。 图 5-5 比例微分环节 (1+ Ts) 的伯德图