
导 3)面面距离:如果平面a与平面B平行,n是平面B的一个法 向量(当然也是平面a的一个法向量),A和B分别是平面a与 平面B内的点,则平面a与平面B之间的距离为BAm (4)两,点间的距离:已知点A(c1y1,Z1),B(x2y2,2),则A,B两点间 的距离为AB=x2x12+y2-y12+(亿2-212
导航 (3)面面距离:如果平面 α 与平面 β 平行,n 是平面 β 的一个法 向量(当然也是平面 α 的一个法向量),A 和 B 分别是平面 α 与 平面 β 内的点,则平面 α 与平面 β 之间的距离为 d=|𝑩 𝑨 ·𝒏| |𝒏| . (4)两点间的距离:已知点 A(x1,y1,z1),B(x2,y2,z2),则 A,B 两点间 的距离为|𝑨 𝑩 |= (𝒙𝟐-𝒙𝟏) 𝟐 + (𝒚𝟐-𝒚𝟏) 𝟐 + (𝒛𝟐-𝒛𝟏) 𝟐

导航 【思考辨析】 判断正误(正确的画“V,错误的画“×”) (1)单位向量都相等( (2)若两向量相等,则它们的模相等() (3)对于任意一个非零向量a,a(2∈R)可以表示所有与a共线 的向量()
导航 【思考辨析】 判断正误.(正确的画“ ”,错误的画“×”) (1)单位向量都相等.( × ) (2)若两向量相等,则它们的模相等.( ) (3)对于任意一个非零向量a,λa(λ∈R)可以表示所有与a共线 的向量.( )

导航 (4)零向量与任意两个向量共面.() (⑤)若两直线的方向向量平行,则两直线平行.( (6)若两平面的法向量垂直,则两平面垂直.() ()二面角的大小等于其两半平面的法向量的夹角.( (8)若平面a平面B,则a上任意一点到平面的距离都等于a,P 之间的距离.()
导航 (4)零向量与任意两个向量共面.( ) (5)若两直线的方向向量平行,则两直线平行.( × ) (6)若两平面的法向量垂直,则两平面垂直.( ) (7)二面角的大小等于其两半平面的法向量的夹角.( × ) (8)若平面α∥平面β,则α上任意一点到平面β的距离都等于α,β 之间的距离.( )
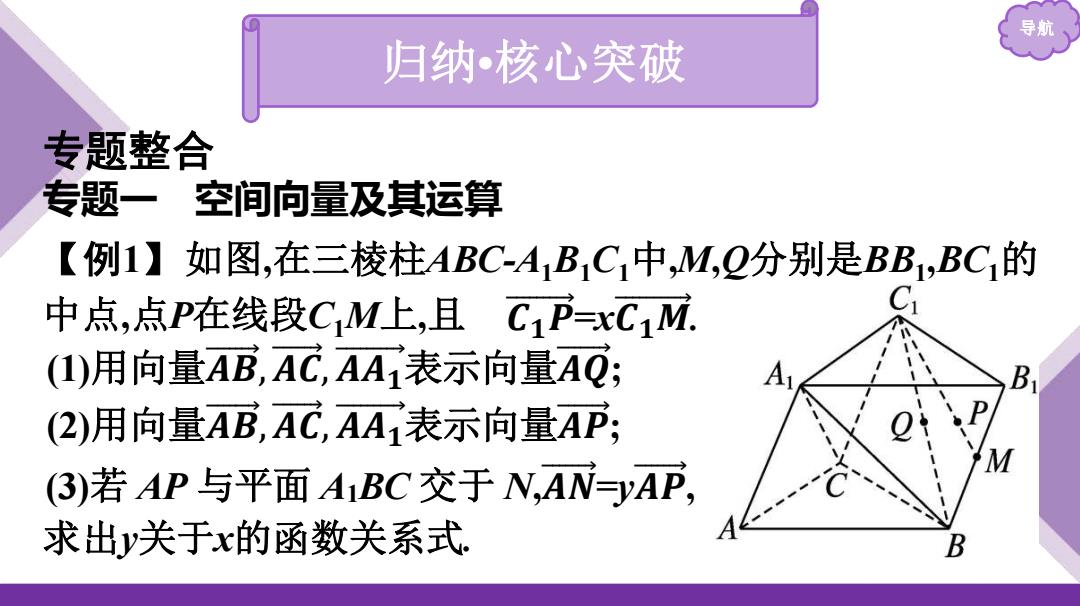
导 归纳核心突破 专题整合 专题一空间向量及其运算 【例1】如图,在三棱柱ABC-A1B1C1中,M,Q分别是BB1,BC1的 中点,点P在线段CM上,且C1P=xC1M. C (1)用向量AB,AC,AA表示向量AQ; A (2)用向量AB,AC,AA1表示向量AP; (3)若AP与平面A1BC交于N,AN=yAP, 求出y关于x的函数关系式 B
导航 归纳•核心突破 专题整合 专题一 空间向量及其运算 【例1】如图,在三棱柱ABC-A1B1C1中,M,Q分别是BB1 ,BC1的 中点,点P在线段C1M上,且 𝑪 𝟏 𝑷 =x𝑪 𝟏 𝑴 . (1)用向量𝑨 𝑩 ,𝑨 𝑪 , 𝑨𝑨𝟏 表示向量𝑨 𝑸 ; (2)用向量𝑨 𝑩 ,𝑨 𝑪 , 𝑨𝑨𝟏 表示向量𝑨 𝑷 ; (3)若 AP 与平面 A1BC 交于 N,𝑨 𝑵 =y𝑨 𝑷 , 求出y关于x的函数关系式

导航 分析:可借助于三角形法则、平行四边形法则求解(1)2)两问, 借助共面向量定理解答(③) 解:(1)A0=AE+B0=AE+2BC -AB+(ACi-AB)-AB+ACi-AB 4B +AAi+ac (AB+AAi+AC)
导航 分析:可借助于三角形法则、平行四边形法则求解(1)(2)两问; 借助共面向量定理解答(3). 解:(1)𝑨 𝑸 = 𝑨 𝑩 + 𝑩 𝑸 = 𝑨 𝑩 + 𝟏 𝟐 𝑩𝑪𝟏 =𝑨 𝑩 + 𝟏 𝟐 (𝑨𝑪𝟏 − 𝑨 𝑩 )=𝑨 𝑩 + 𝟏 𝟐 𝑨𝑪𝟏 − 𝟏 𝟐 𝑨 𝑩 = 𝟏 𝟐 𝑨 𝑩 + 𝟏 𝟐 𝑨𝑨𝟏 + 𝟏 𝟐 𝑨 𝑪 = 𝟏 𝟐 (𝑨 𝑩 + 𝑨𝑨𝟏 + 𝑨 𝑪 )