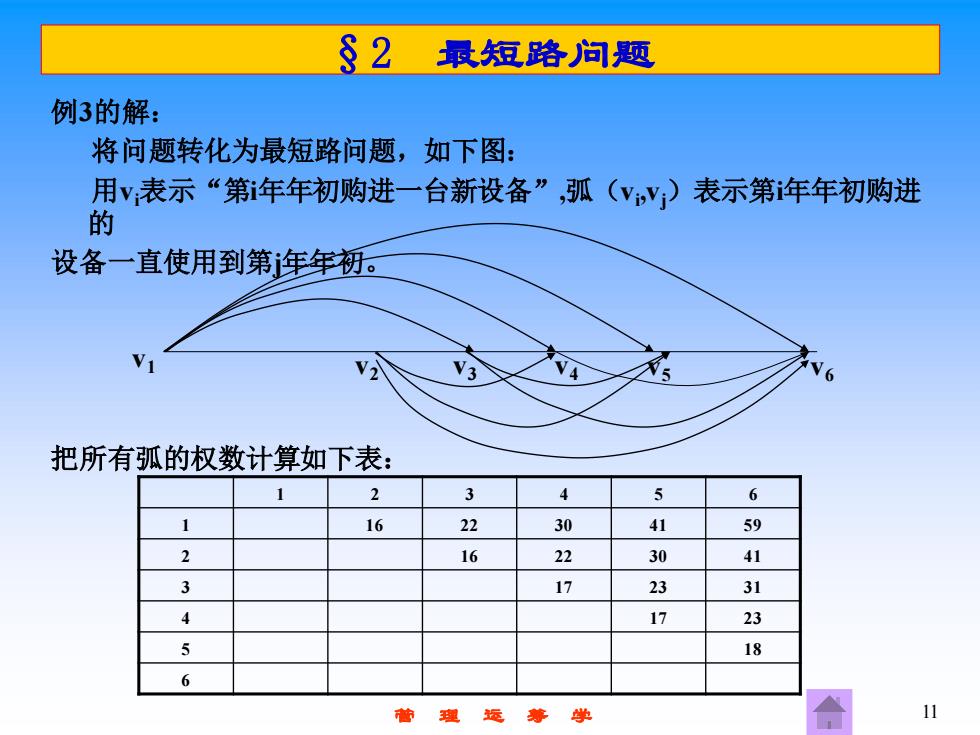
§2 最短路问题 例3的解: 将问题转化为最短路问题,如下图: 用v表示“第年年初购进一台新设备”,弧(V,y)表示第年年初购进 的 设备一直使用到第年年初。 V3 4 把所有弧的权数计算如下表: 1 3 5 6 16 22 30 59 3 16 22 30 41 3 17 23 31 4 17 23 5 18 6 曹理远茅学 11
管 理 运 筹 学 11 §2 最短路问题 例3的解: 将问题转化为最短路问题,如下图: 用vi表示“第i年年初购进一台新设备”,弧(vi ,vj)表示第i年年初购进 的 设备一直使用到第j年年初。 把所有弧的权数计算如下表: v1 v2 v3 v4 v5 v6 1 2 3 4 5 6 1 16 22 30 41 59 2 16 22 30 41 3 17 23 31 4 17 23 5 18 6
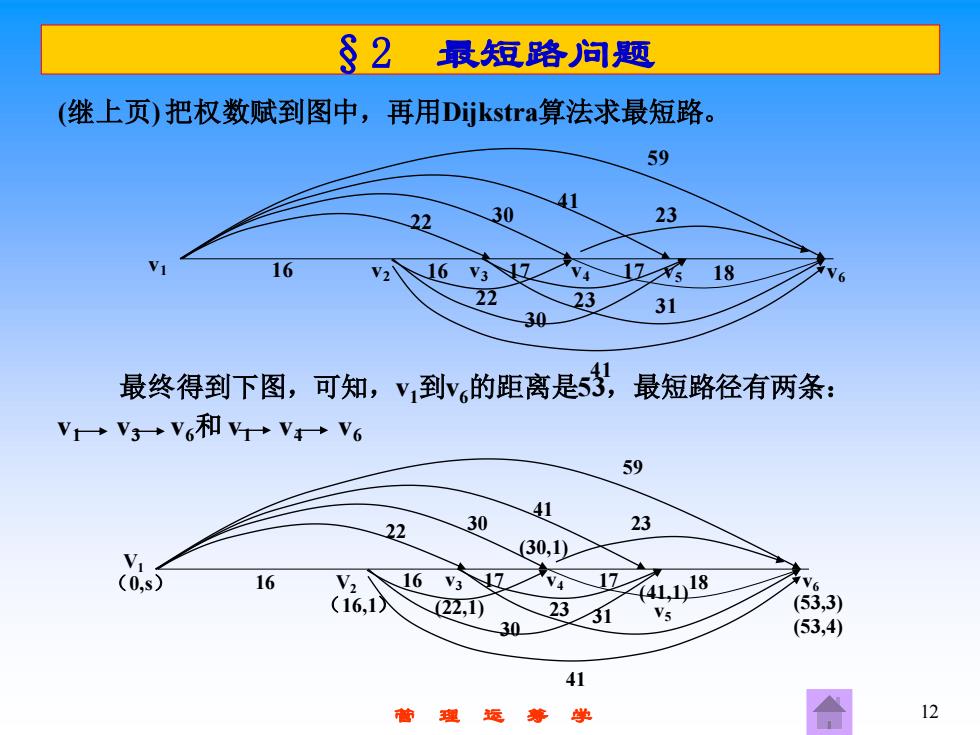
§2 最短路问题 (继上页)把权数赋到图中,再用Dijkstra2算法求最短路。 59 41 22 30 23 16 16V3 118 22 23 31 30 最终得到下图,可知,v到v,的距离是53, 最短路径有两条: V1→V3→V和V+V6 59 41 22 30 23 30,1) 16 16 8 6 (16.1 22,1 2351 (53,3) 30 (53,4) 41 学 12
管 理 运 筹 学 12 §2 最短路问题 (继上页) 把权数赋到图中,再用Dijkstra算法求最短路。 最终得到下图,可知,v1到v6的距离是53,最短路径有两条: v1 v3 v6和 v1 v4 v6 v1 v2 v3 v4 v5 v6 16 22 30 41 59 16 22 30 41 31 23 17 17 18 23 V1 (0,s) v3 v4 (41,1) v5 v6 22 30 41 59 16 (22,1) 30 41 31 23 17 17 18 23 V2 (16,1) 16 (30,1) (53,3) (53,4)
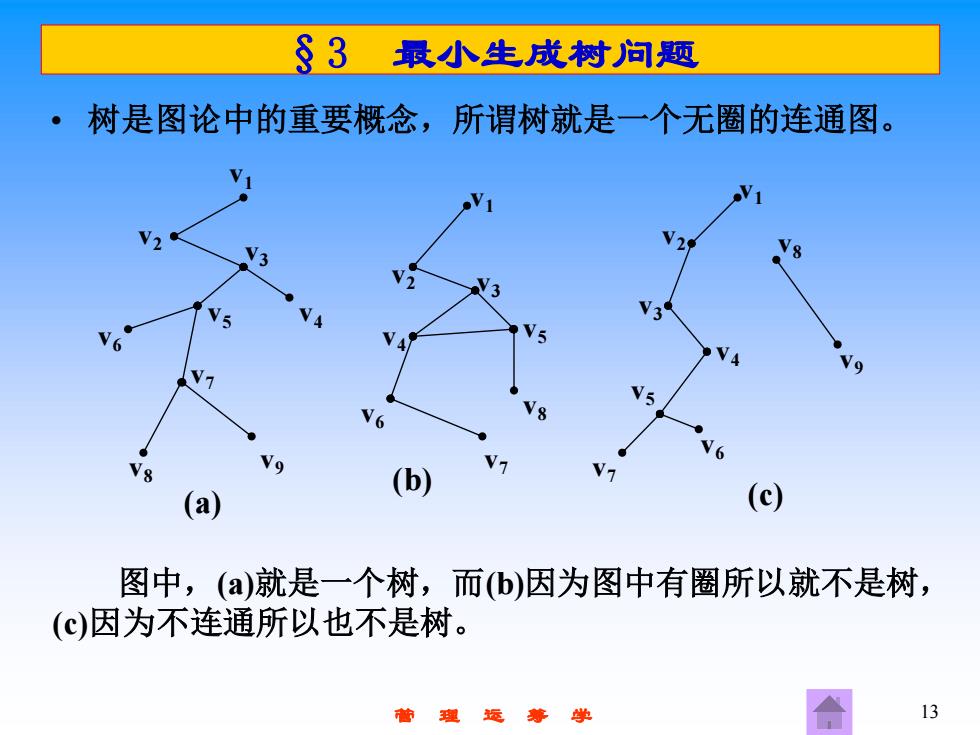
§3 最小生成树问题 树是图论中的重要概念,所谓树就是一个无圈的连通图。 ● V5 V3 6 5 V] V5 9 (b) a (c) 图中,(a)就是一个树,而(b)因为图中有圈所以就不是树, ()因为不连通所以也不是树。 13
管 理 运 筹 学 13 §3 最小生成树问题 • 树是图论中的重要概念,所谓树就是一个无圈的连通图。 图中,(a)就是一个树,而(b)因为图中有圈所以就不是树, (c)因为不连通所以也不是树。 v1 v2 v3 v5 v4 v6 v7 v8 v9 v1 v2 v3 v5 v8 v7 v6 v4 v1 v2 v3 v4 v5 v7 v6 v8 v9 (a) (b) (c)