
前面的例 例5 求微分方程y”-y2=0的通解 解二 两端同乘不为零因子 故y'=C1y, 涵 从而通解为y=C2ecx
解 二 , 1 2 y 两端同乘不为零因子 2 2 0, d dx yy y y y y = = − , 1 故 y = C y 从而通解为 . 1 2 C x y = C e 0 . 例 5 求微分方程 yy − y 2 = 的通解 前面的例 3

之例5求微分方程少”-y2=0的通解 解三原方程变为 1 两边积分,得 In y'=In y+InC 即y=Cy, 极秋私 原方程通解为 y= #
解 三 原方程变为 , y y y y = 两边积分,得 ln y = ln y + lnC1, 即 y = C1 y, 原方程通解为 . 1 2 C x y = C e 0 . 例 5 求微分方程 yy − y 2 = 的通解 #
6.4二阶常系数线性齐次微分方程 6.4.1二阶常系数线性微分方程的概念 6.4.2二阶常系数线性齐次微分方程解的结构 6.4.3二阶常系数线性齐次微分方程的解法 y”+py'+9y=0 极极
6.4.1 二阶常系数线性微分方程的概念 6.4.2 二阶常系数线性齐次微分方程解的结构 6.4.3 二阶常系数线性齐次微分方程的解法 6.4 二阶常系数线性齐次微分方程 y p y q y + + = 0

6.4.1二阶常系数线性微分方程的概念 二阶线性微分方程的标准形式 y”+p(x)y+q(x)y=f(x) 阶常系数线性微分方程的标准形式 秋私 y+py+qy=f(x)其中p,q是常数
二阶线性微分方程的标准形式 二阶常系数线性微分方程的标准形式 6.4.1 二阶常系数线性微分方程的概念 其中 p,q 是常数 y p x y q x y f x + + = ( ) ( ) ( ) y y + + = p q y f ( x)
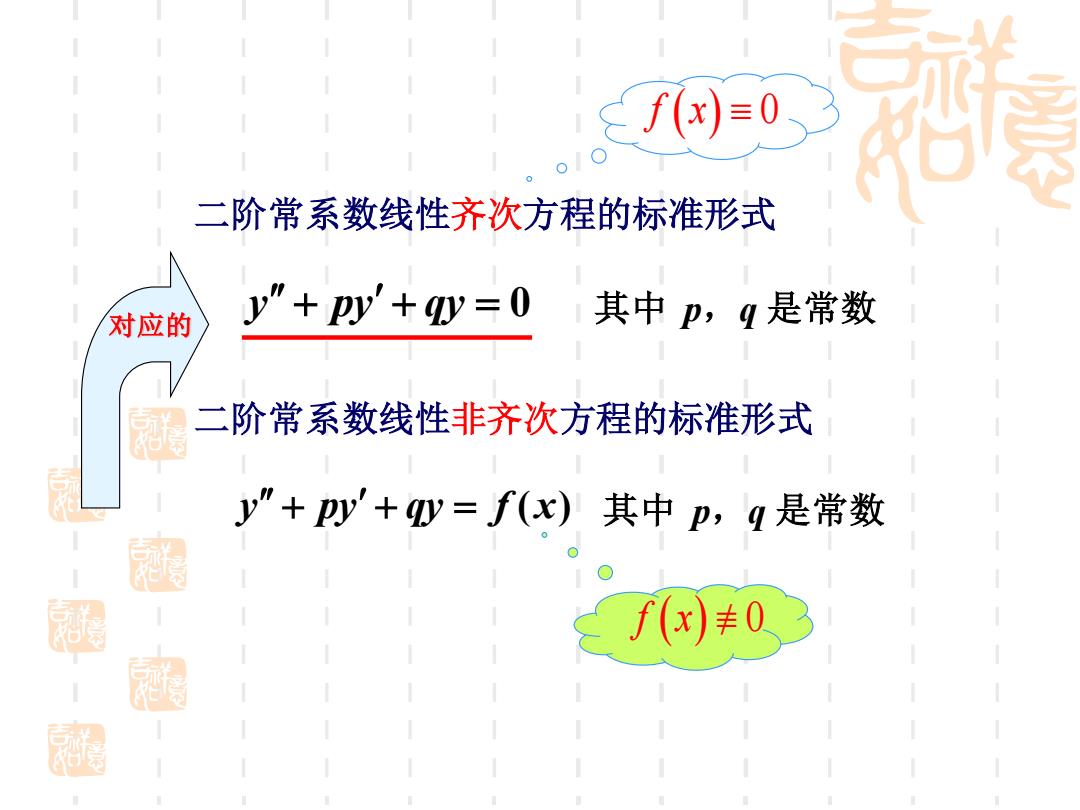
f(x)=0 二阶常系数线性齐次方程的标准形式 对应的 y”+py'+y=0 其中p,q是常数 二阶常系数线性非齐次方程的标准形式 y”+py'+y=f(x)其中p,q是常数 极汉 f(x)丰0
y + py + qy = 0 二阶常系数线性齐次方程的标准形式 y + py + qy = f (x) 二阶常系数线性非齐次方程的标准形式 其中 p,q 是常数 其中 p,q 是常数 f x( ) 0 对应的 f x( ) 0