
梯度向量、梯度算子 设f(x)在点x可微,则称向量 af af …x 为函数f(x)在点x的梯度向量, 简称梯度,记作grad或V/,即gradf=-Vf一 f af a 而把 叫做梯度算子,记作grad或V,此时,方向导数 of-vf.u Ou 即为grad在u方向的投影。 O 故gradfi的方向指向函数值变化最快的方向,长度为f在此方向上的变化率
梯度向量、梯度算子 1 1 1 ( ) , , ( ) grad grad = = , , , , grad gr d ad = a gr n n n f f f f f x x f f f f f f x x x x f f f f f x x x x u u u u 设 在点 可微,则称向量 为函数 在点 的梯度向量, 简称梯度,记作 或 ,即 而把 叫做梯度算子,记作 或 ,此时,方向导数 ,即 为 在 方向的投影。 故 的方向指向函数值变化最快的方向,长度为 在此方向上的变化率
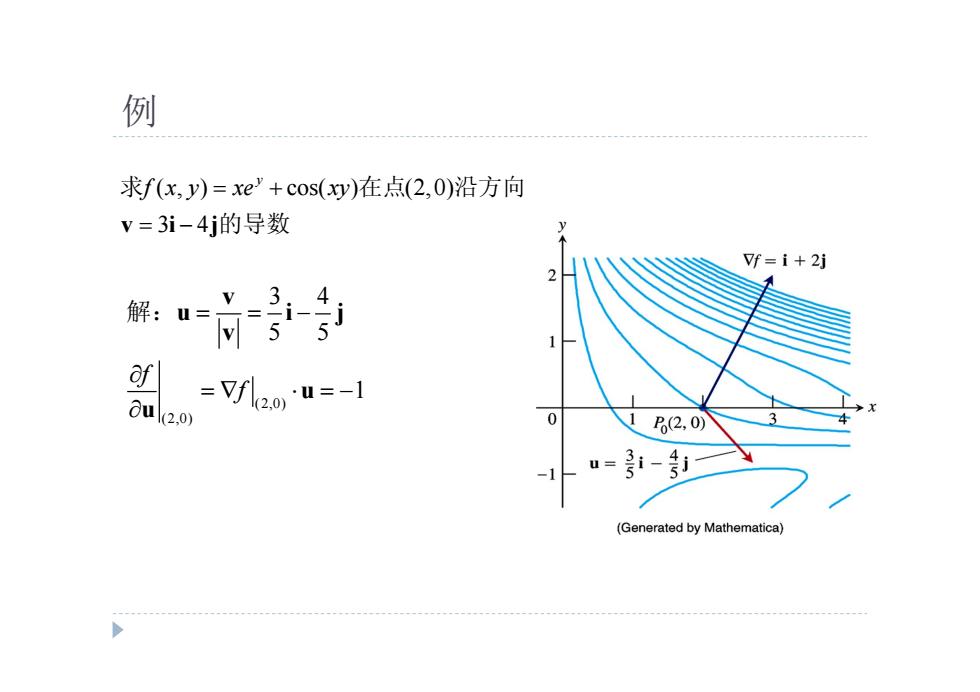
例 求f(x,y)=xe'+cos(xy)在点(2,0)沿方向 v=3i-4j的导数 Vf=i+2j af =Vflao'u=-1 u2.0) 0 1 (2,0) u=i- (Generated by Mathematica)
例 ( , ) cos( ) (2,0) 3 4 y f x y xe xy v i j 求 在点 沿方向 的导数 (2,0) (2,0) 3 4 5 5 1 f f v u i j v u u 解:
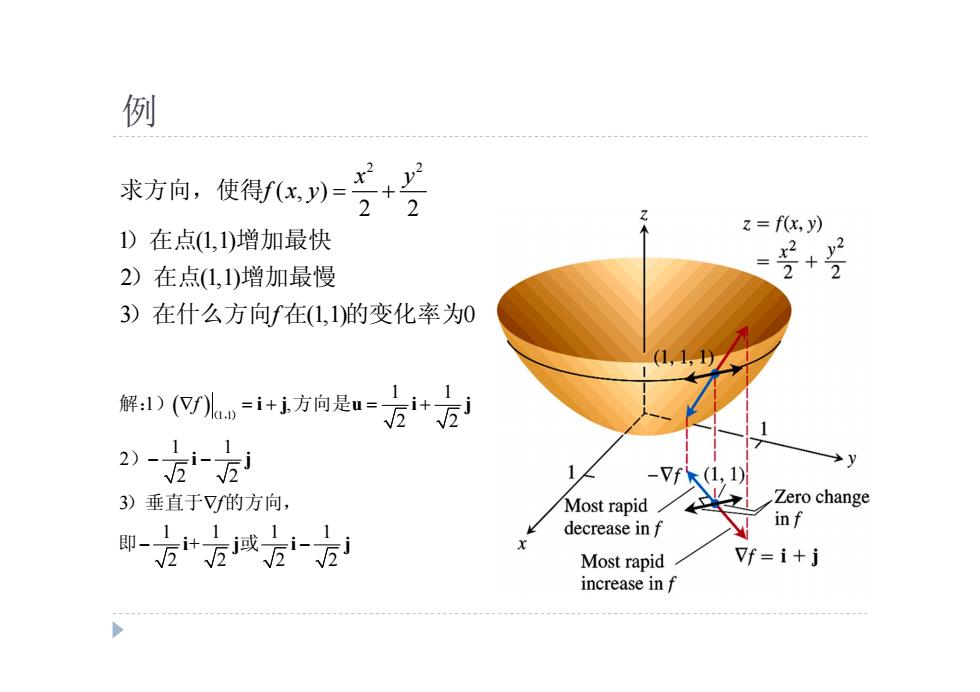
例 求方向, 使得fx川=之+2 x2 y2 z=f(x,y) 1)在点1,1)增加最快 2)在点(1,1)增加最慢 苦+ 3)在什么方向f在(1,1)的变化率为0 (1,1,1) 解D0.=i4i方向是u=方+方 →y -7fk(1,1) 3)垂直于f的方向, Most rapid Zero change decrease in f inf 即方方方 Most rapid Vf=i+j increase in f
例 2 2 ( , ) 2 2 1 (1,1) 2 (1,1) 3 (1,1) 0 x y f x y f 求方向,使得 )在点 增加最快 )在点 增加最慢 )在什么方向 在 的变化率为 1 1 1 1 1 , 2 2 1 1 2 2 2 3 1 1 1 1 + 2 2 2 2 f f i j u i j i j i j i j 解:) ( ,) 方向是 ) )垂直于 的方向, 即 或

等高线与梯度的关系 在f(x,y)的定义域的每个点(x,,),正交于过(x,y,)的等高线 等高线:r=g(t)i+ht)j,函数f在其上取常数值c, /(e0e)-0即竖+影h-0 ox dt oy dt The curve f(x,y)=f(oo) (xo.Yo) Vf(xo.Yo) 1、曲线f(x,y)=0上过(xo,)点的切线方程 f(x,%)(x-x)+f(x,)(y-)=0 2、曲面F(xy,)=0,法向量:(F(x0,),F(x,,2o,F(x%,2o) 切平面:F((x-6)+aF(0y-为)+F(e-)=0 Ox
等高线与梯度的关系 0 0 0 0 在f x y x y x y ( , ) ( , ) ( , ) 的定义域的每个点 ,正交于过 的等高线 ( ) ( ) , ( ), ( ) 0, 0 0 g t h t f c d f dg f dh f g t h t dt x dt y dt dg dh f dt dt r i j i j 等高线: ,函数 在其上取常数值 即 故 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ( , ) ( , ) ( , , 1 ( , ) 0 ( , ) 0 2 ( , , ) 0 ( , , ), ( , , ), ( , , ) ( ) ( ) ( , ) ( ) , ) ( , , ) 0 x y x y z f x y f x y F x y z F x y z F x y z x f x y x y x x y y F x y z F x y z F x y z F x y z x x y y y z z z 、曲线 上过 点的切线方程 、曲面 ,法向量: 切平面:

全微分的几何意义 曲面z=f(x,y)在M(x,,二)存在不平行于z轴的切平面的充分必要 条件是:f(xy)在(xo,y)可微,此时切平面方程为 --)-W 由此全微分的几何意义是切平面的竖坐标的对应的改变量
全微分的几何意义 0 0 0 0 0 0 0 0 0 0 0 0 0 ( , ) ( , , ) ( , ) ( , ) ( , ) ( , ) z f x y M x y z z f x y x y f x y f x y z x x y y x y z 曲面 在 存在不平行于 轴的切平面的充分必要 条件是: 在 可微,此时切平面方程为 由此全微分的几何意义是切平面的竖坐标的对应的改变量