
例2-15:试求电枢控制直流电动机的传递函数 doa@+0n(0)=Kn4,④-K.M.0 dt 解: 根据线性叠加原理,分别研究U()到om()和M()到 om(t)的传递函数 G(S)= 2 (s) Km U(s)Ts+1 66- 2m(s)_-K。 M.(s) T.s+1
例2-15: 试求电枢控制直流电动机的传递函数 ( ) ( ) ( ) ( ) t K u t K M t dt d t T m m a c c m m + = − ( ) 1 ( ) ( ) + = = T s K U s s G s m m a m ( ) 1 ( ) ( ) + − = = T s K M s s G s m c c m m U (t) 根据线性叠加原理,分别研究 a 到 和 到 的传递函数 (t) m M (t) c (t) m 解:
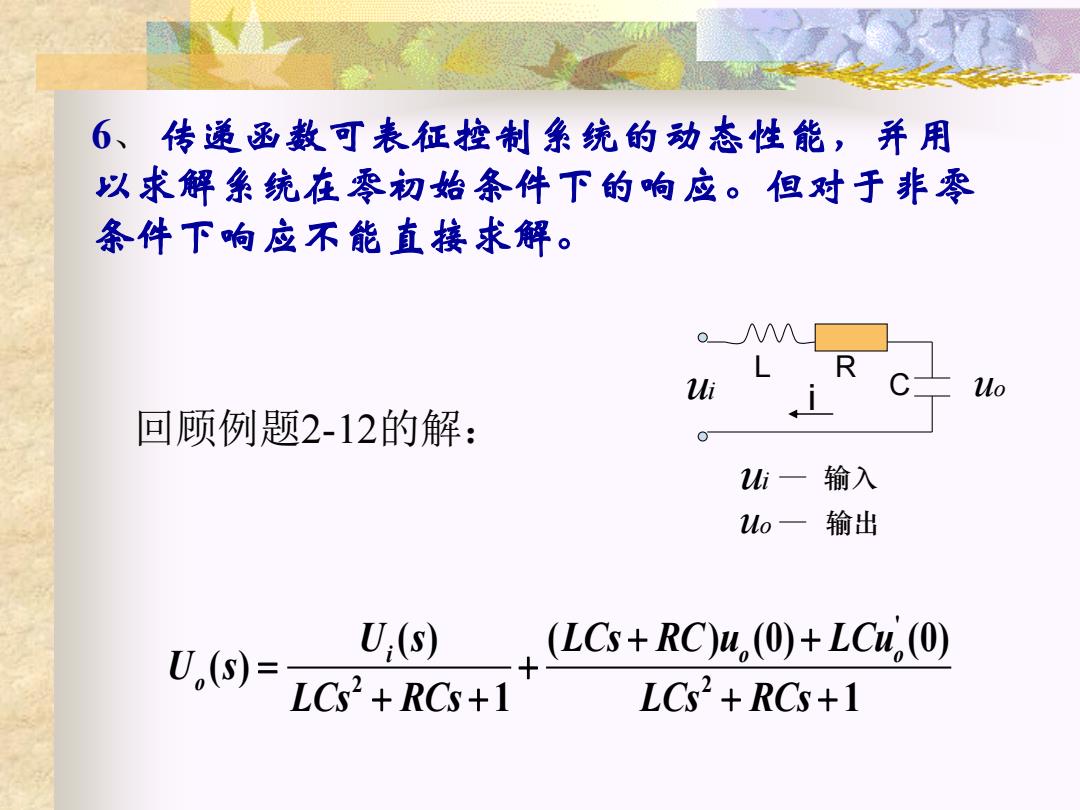
6、传递函数可表征控制系统的动态性能,并用 以求解条统在零初始条件下的响应。但对于非零 条件下响应不能直接求解。 Mi Mo 回顾例题2-12的解: Wi 一输入 1o一输出 U,(s)= U,(s) (LCs+RC)u (0)+LCu,(0) LCs2+RCs+1 LCs+RCs+1
6、 传递函数可表征控制系统的动态性能,并用 以求解系统在零初始条件下的响应。但对于非零 条件下响应不能直接求解。 ' 2 2 ( ) ( ) (0) (0) ( ) 1 1 i o o o U s LCs RC u LCu U s LCs RCs LCs RCs + + = + + + + + ui 输入 uo 输出 ui uo L R C i 回顾例题2-12的解:

2.传递函数的零点与极点 C(s) G(s)= b,s"+b,sm-1+…+bm5+bm M(s) R(s) S”+aS-+…+0n-1S+0n N(s) b6-5-3)6-= Π6-z) K*i (s-P1)s-P2)…(S-pm) Πs-p) i=1 X bo X22 Zi ao 零极点分布图 称为传递系数或根轨迹增益
2. 传递函数的零点与极点 1 0 1 1 1 0 1 1 0 1 2 1 * 0 1 2 1 ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) ( )( ) ( ) ( ) m m m m n n n n m i m i n n j j C s M s b s b s b s b G s R s a s a s a s a N s s z b s z s z s z K a s p s p s p s p − − − − = = + + + + = = + + + + − − − − = = − − − − j 0 z2 z1 零极点分布图 0 * 0 a b K = 称为传递系数或根轨迹增益

传递函数也可写成如下连乘积的形式 C(s) bosm+bs+bm-is+bm G(S)= R(s) a0s”+a1s”+…+an-1S+an bm(t1s+1(zs2+252t2S+1)…(tS+1) an(T1s+1T3s2+252T2s+1)…(TjS+1) K 称为传递系数或增益或放大系数。 An 在单位阶跃作用下,系统的稳态输出即 为K
n m a b K = ( 1)( 2 1) ( 1) ( 1)( 2 1) ( 1) ( ) ( ) ( ) 2 2 2 2 1 2 2 2 2 2 1 2 1 1 0 1 1 1 0 1 + + + + + + + + = + + + + + + + + = = − − − − a T s T s T s T s b s s s s a s a s a s a b s b s b s b R s C s G s n j m i n n n n m m m m 传递函数也可写成如下连乘积的形式 称为传递系数或增益或放大系数。 在单位阶跃作用下,系统的稳态输出即 为K