
例2-9:图为弹簧-质量-阻尼器的机械位移系统,列写质量 在输入量为外力F(),输出量为位移x(t)时的运动方程。 解:根据牛顿第二定律有: d2x F(t-F(t)-F2(t)=m dt2 x(t) E(t)→弹簧恢复力 F()→阻尼器阻力 图2-3机械位移系统
例2-9: 图为弹簧-质量-阻尼器的机械位移系统,列写质量m 在输入量为外力F(t),输出量为位移x(t)时的运动方程。 解:根据牛顿第二定律有: → → − − = (t) 阻尼器阻力 弹簧恢复力 2 1 2 2 1 2 F F t dt d x F t F t F t m ( ) ( ) ( ) ( ) 2 1

F,(t)=kx F(t)=f dx md'x fdx k dt2k dt 十x=Fd)…二阶微分方程 k 比校以上例题的数学模型,可以发现: 二者的数学模型均可用二阶微分方程表示 (相 似系统), 仅方程中系数的大小和其具体的物理含义 不同而已0 启示:1利用电路网络可以模拟仿真非电系统; 2.利用数学模型可以敝开系统的物理属性进行 普遍意义的分析研究
F (t) = kx 2 1 dt dx F (t) = f 1 2 ( ) -------二阶微分方程 1 2 2 F t k x dt dx k f dt d x k m + + = 比较以上例题的数学模型,可以发现: 二者的数学模型均可用二阶微分方程表示(相 似系统),仅方程中系数的大小和其具体的物理含义 不同而已。 启示:1.利用电路网络可以模拟仿真非电系统; 2.利用数学模型可以撇开系统的物理属性进行 普遍意义的分析研究

3.线性系统的基本特性 ■叠加性和齐次性 ■线性系统的性质: 当几个外作用同时加于系统时,可将它们 分别单独处理得出各自的响应,之后将各 响应叠加即为系统总响应。 一个复杂的外作用可分解成若干个简单信 号,求出各简单信号的响应,之后叠加即 得复杂外作用下的响应
3.线性系统的基本特性 ◼ 叠加性和齐次性 ◼ 线性系统的性质: ◼ 当几个外作用同时加于系统时,可将它们 分别单独处理得出各自的响应,之后将各 响应叠加即为系统总响应。 ◼ 一个复杂的外作用可分解成若干个简单信 号,求出各简单信号的响应,之后叠加即 得复杂外作用下的响应
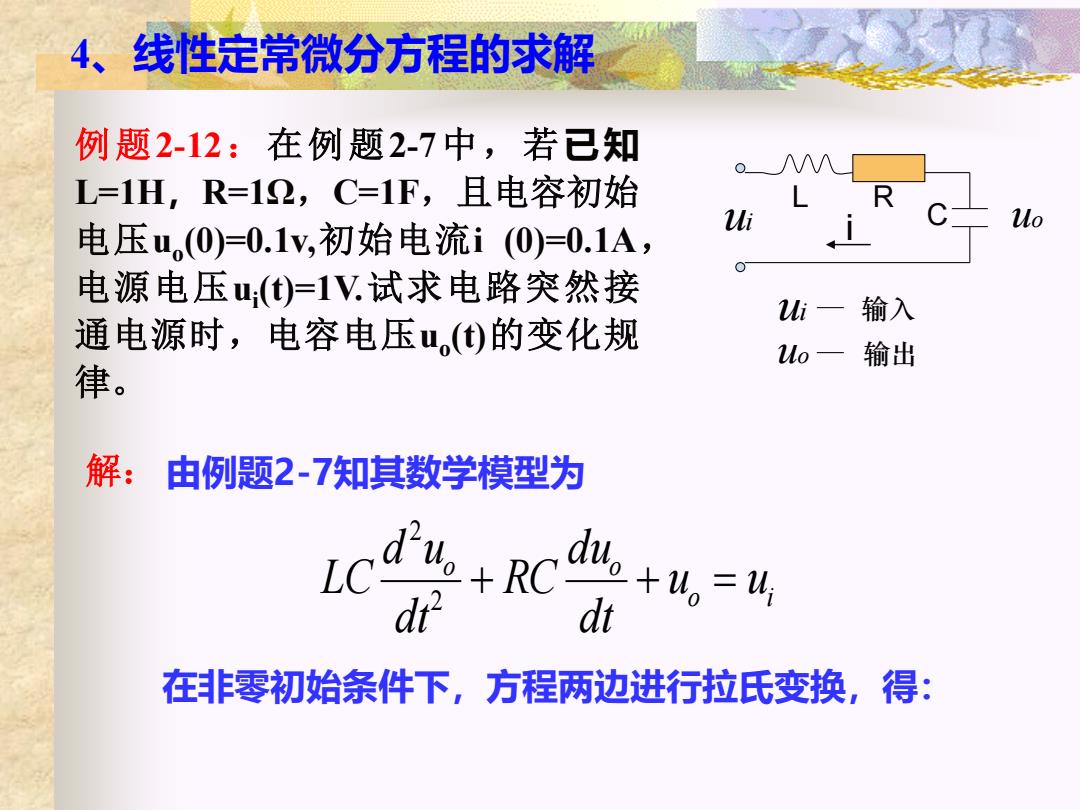
4、线性定常微分方程的求解 例题2-12:在例题2-7中,若已知 L=1H,R=12,C=1F,且电容初始 L 电压u(0)=0.1y,初始电流i(0)=0.1A, Mi 电源电压u()=1V试求电路突然接 1i- 输入 通电源时,电容电压u(①)的变化规 1o一输出 律。 解:由例题2-7知其数学模型为 LCa+RC恤+=4 dr dt 在非零初始条件下,方程两边进行拉氏变换,得:
例题2-12:在例题2-7中,若已知 L=1H,R=1Ω,C=1F,且电容初始 电压uo (0)=0.1v,初始电流i (0)=0.1A, 电源电压ui (t)=1V.试求电路突然接 通电源时,电容电压uo (t)的变化规 律。 解: 在非零初始条件下,方程两边进行拉氏变换,得: 4、线性定常微分方程的求解 ui 输入 uo 输出 ui uo L R C i o i o o u u dt du RC dt d u LC + + = 2 2 由例题2-7知其数学模型为

4、线性定常微分方程的求解 解: 0+c路u LCIs'U,(s)-su,(0)-u,(0]+RC[sU(s)-u(0]+U(s)=U;(s) (LCs2+RCs+1)U,(s)=U;(s)+(LCs+RC)u,(0)+LCu,(0) U,(s)=- U:(S) (LCs+RC)u,(0)+LCu,(0) Cs2+RCs+1 LCs+RCs+1 零状态响应 零输入响应
解: 4、线性定常微分方程的求解 2 ' [ ( ) (0) (0)] [ ( ) (0)] ( ) ( ) LC s U s su u RC sU s u U s U s o o o o o o i − − + − + = o i o o u u dt du RC dt d u LC + + = 2 2 2 ' ( 1) ( ) ( ) ( ) (0) (0) LCs RCs U s U s LCs RC u LCu o i o o + + = + + + ' 2 2 ( ) ( ) (0) (0) ( ) 1 1 i o o o U s LCs RC u LCu U s LCs RCs LCs RCs + + = + + + + + 零状态响应 零输入响应