
否则,若M由某一点M出发,沿S上某一封闭曲线 回是省替签方向与出发时的方向相反则客 通常遇到的曲面大多是双侧曲面.单侧曲面的 一个典型例子是默比乌斯M6bius)带.它的构造方 法如下:取一矩形长纸条ABCD(如图22-4(a),将其 一 端扭转180°后与另一端粘合在一起(即让A与C 重合,B与D重合,如图22-4(b)所示). 前页 后页 返回
前页 后页 返回 否则, 若 M 由某一点 M0 出发, 沿S 上某一封闭曲线 回到 时, 其法线方向与出发时的方向相反, 则称 S 是单侧曲面. 通常遇到的曲面大多是双侧曲面. 单侧曲面的 一个典型例子是默比乌斯(Möbius)带. 它的构造方 法如下: 取一矩形长纸条ABCD (如图22-4(a)), 将其 一端扭转 180 后与另一端粘合在一起(即让A与C 重合, B与D重合, 如图22-4(b)所示). M0
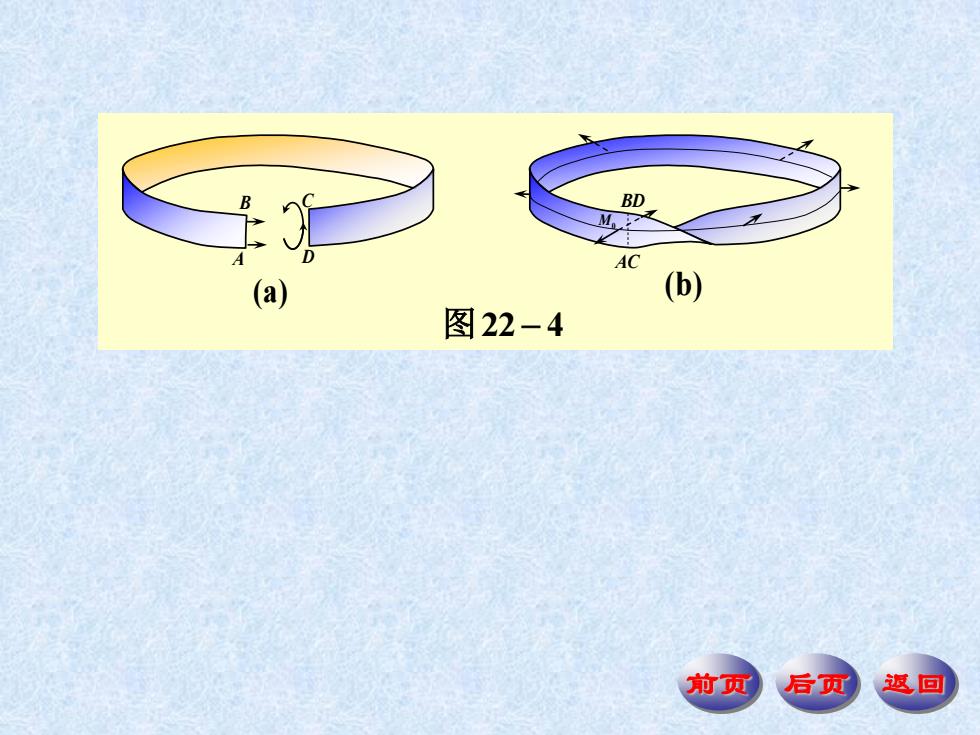
BD (a) (b) 图22-4 前页 后顶 返回
前页 后页 返回 图22 4 A B C D (a) ACBD M0 (b)

通常由z=(x,y)所表示的曲面都是双侧曲面,其法 线方向与z轴正向的夹角成锐角的一侧称为上侧, 另一侧称为下侧.当S为封闭曲面时,法线方向朝外 的一侧称为外侧,另一侧称为内侧.习惯上把上侧 作为正侧,下侧作为负侧;又把封闭曲面的外侧作为 正侧,内侧作为负侧. 前页 后页 返回
前页 后页 返回 通常由 z z x y ( , ) 所表示的曲面都是双侧曲面, 其法 线方向与 z 轴正向的夹角成锐角的一侧称为上侧, 另一侧称为下侧. 当 S 为封闭曲面时,法线方向朝外 的一侧称为外侧,另一侧称为内侧. 习惯上把上侧 作为正侧,下侧作为负侧;又把封闭曲面的外侧作为 正侧, 内侧作为负侧