
二、第一型曲面积分的计算 第一型曲面积分可化为二重积分来计算. 定理22.1设有光滑曲面 S:z=z(x,y),(x,y)∈D, f(x,y,z)为S上的连续函数,则 /.zs=∬fx,2++ad. …(2) 前页 后 返回
前页 后页 返回 二、第一型曲面积分的计算 第一型曲面积分可化为二重积分来计算. 定理22.1 设有光滑曲面 S z zxy xy D : ( , ),( , ) , = ∈ f xyz (, ,) 为S上的连续函数, 则 2 2 ( , , )d ( , , ( , )) 1 d d . x y S D f xyz S f xyzxy z z x y = + + ∫∫ ∫∫ (2)
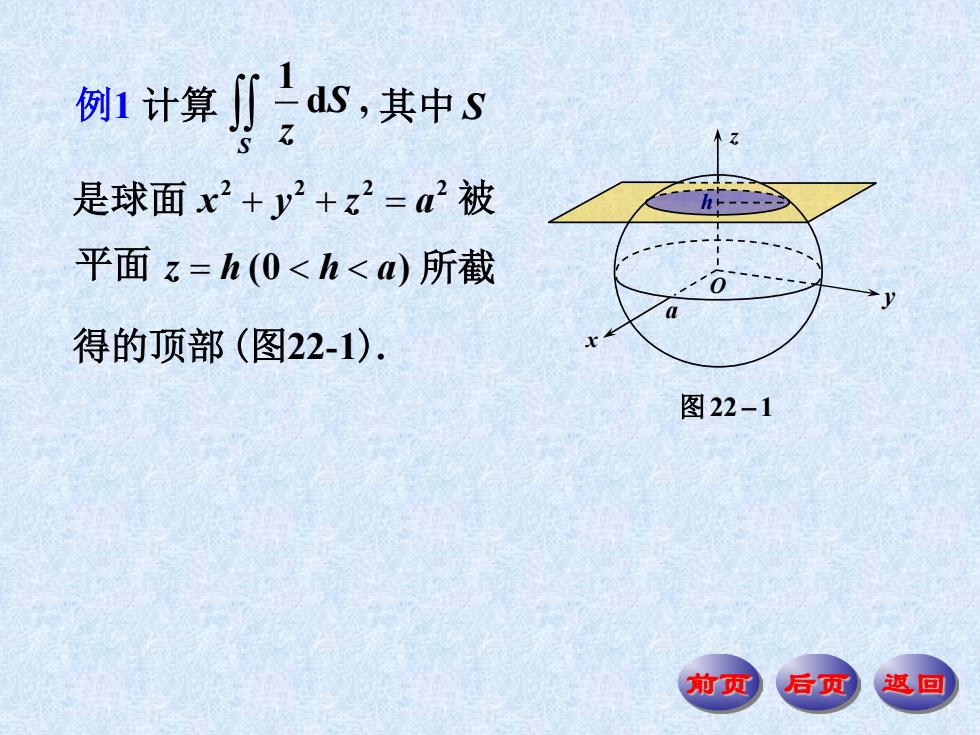
例1计算,ds,其中s 是球面x2+y2+z2=a2被 平面z=h(0<h<)所截 得的顶部(图22-1). 图22-1 前页 后页 返回
前页 后页 返回 1 d , S S z 例1 计算 ∫∫ 其中 S 2 22 2 是球面 xyza ++= 被 平面 zh ha = << (0 ) 所截 得的顶部(图22-1). x y h O z a 图 22 1 −

例2计算∬(y+zx+z)dS, 其中S为圆锥面z=√x2+少 =x+y 被圆柱面x2+y2=2x所割 下的部分(图22-2). x2+y2=2x 图22-2 前页 后页 返回
前页 后页 返回 例2 计算 ( )d , S xy zx yz S + + ∫∫ S 2 2 其中 为圆锥面 z xy = + 被圆柱面 2 2 x y ax + = 2 所割 下的部分(图22-2). 图22 2 − y x O 2 2 z xy = + 2 2 x y ax + = 2 z

§2第二型曲面积分 教学内容: 一、曲面的侧 二、第二型曲面积分的概念 三、第二型曲面积分的计算 前页 后页 返回
前页 后页 返回 §2 第二型曲面积分 教学内容: 一、曲面的侧 二、第二型曲面积分的概念 三、第二型曲面积分的计算 返回

一、曲面的侧 设连通曲面S上到处都有连续变动的切平面(或法 线),曲面在其上每一点处的法线有两个方向:当取 定其中一个指向为正方向时,另一个指向就是负方 向.又设M,为S上任一点,L为S上任一经过点M, 且不超出S边界的闭曲线.当S上的动点M从M。 出发沿L连续移动一周而回到时,如果有如下特 征:出发时M与M取相同的法线方向,而回来时仍 保持原来的法线方向不变,则称该曲面S是双侧的. 前页 返回
前页 后页 返回 一、曲面的侧 设连通曲面S 上到处都有连续变动的切平面 (或法 线), 曲面在其上每一点处的法线有两个方向:当取 定其中一个指向为正方向时, 另一个指向就是负方 向. 又设 M0 为S 上任一点, L为 S上任一经过点 0 M , 且不超出 S 边界的闭曲线. 当S 上的动点M 从 M0 出发沿 L 连续移动一周而回到 时,如果有如下特 M0 征 M0 :出发时 M 与 取相同的法线方向, 而回来时仍 保持原来的法线方向不变,则称该曲面 S 是双侧的