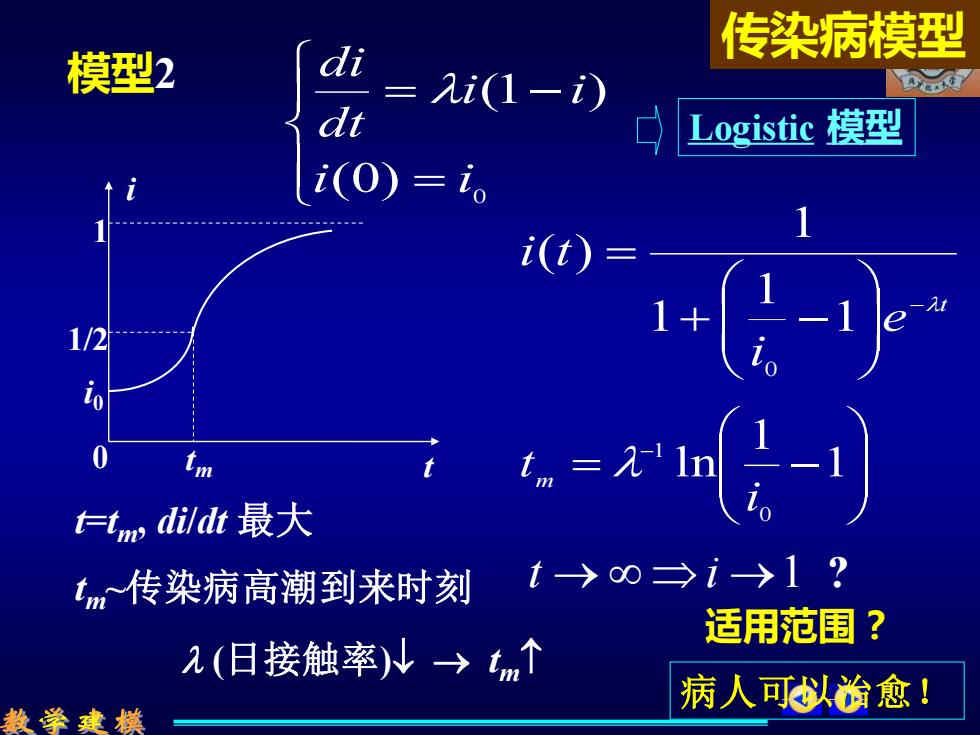
传染病模型 模型2 di =入i(1-) Logistic模型 i(0)=。 i(t) 1/2 1+ tm n=元'lm t dildt最大 tm传染病高潮到来时刻 t→0→i→1? 适用范围? 2(日接触率)N→tm个 病人可以治愈! 数学建模
t e i i t − + − = 1 1 1 1 ( ) 0 = = − 0 (0) (1 ) i i i i dt di 模型 2 1/2 tm i i0 1 0 t = − − 1 1 ln 0 1 i t m tm~传染病高潮到来时刻 (日接触率) → tm t → i →1 Logistic 模型 病人可以治愈! ? t=tm, di/dt 最大 传染病模型 适用范围?

传染病模型 模型3 传染病无免疫性—病人治愈成 为健康人,健康人可再次被感染 SIS模型 增加假设 3)病人每天治愈的比例为4 4~日治愈率 建模 W[i(t+△t)-i(t)]=2Ns(t)i(t)△t-Ni(t)△i di =入i(1-)-10 入~日接触率 i(0)=i。 1/4~感染期 o=λ/4 。~一个感染期内每个病人的 有效接触人数,称为接触数。 数学建模
模型3 传染病无免疫性——病人治愈成 为健康人,健康人可再次被感染 增加假设 SIS 模型 3)病人每天治愈的比例为 ~日治愈率 建模 N[i(t + t) −i(t)] = Ns(t)i(t)t − Ni(t)t = / ~ 日接触率 1/ ~感染期 ~ 一个感染期内每个病人的 有效接触人数,称为接触数。 = = − − 0 (0) (1 ) i i i i i dt di 传染病模型