
第四章非线性方程求根 2
2 第四章 非线性方程求根
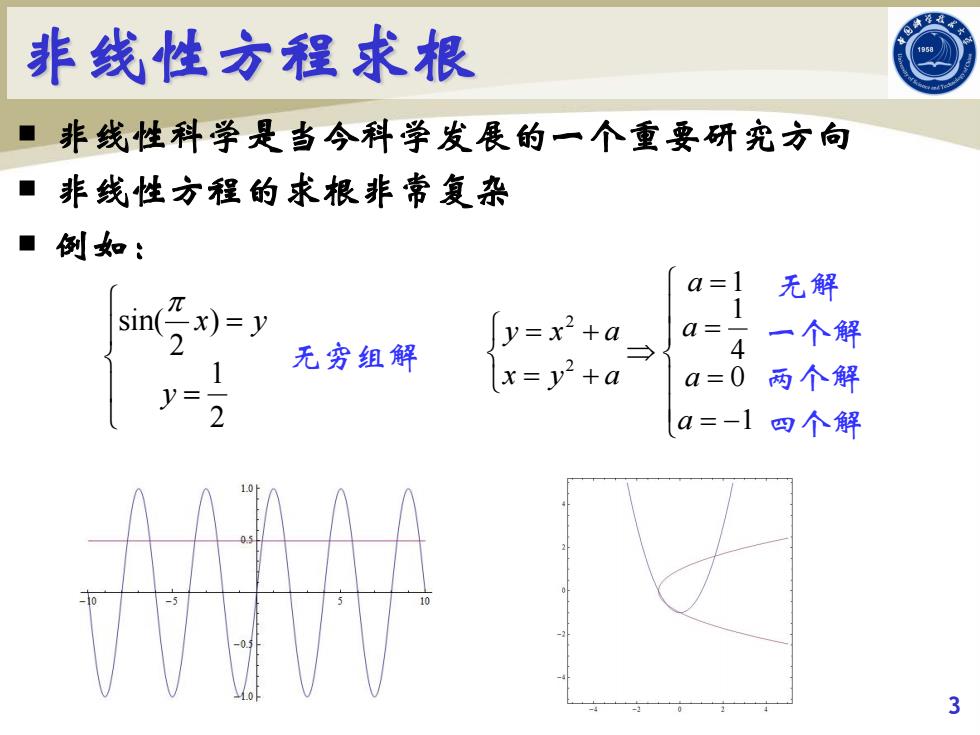
非线性方程求根 非线性科学是当今科学发展的一个重要研究方向 非线性方程的求根非常复杂 ■例如: a= 无解 2 sin(x)=y 1 2 y=x2+a Q= -4 一个解 无穷组解 1 x=y2+a a=0 两个解 y= 2 a=-1四个解 3
非线性方程求根 非线性科学是当今科学发展的一个重要研究方向 非线性方程的求根非常复杂 例如: 3 = = 2 1 ) 2 sin( y x y π 无穷组解 = − = = = ⇒ = + = + 1 0 4 1 1 2 2 a a a a x y a y x a 无解 一个解 两个解 四个解

非线性方程求根 ■非线性方程的根通常不止一个,很唯找到所有的解 ·非线性方程求根,通常需要给定初始值或求解范围, 用送代法求解 ■(介值定理)设f(x)是区间[a,b]上的一个连续函数, 那么f(x)取到f(a与f(b)之间的任何一个值,即如果y 是f(a)与f(b)之间的一个数,那么存在一个数c∈[a,b] 使得f(c)=y (推论)f(a)f(b)<0→3x,s.t,f(x)=0 4
非线性方程求根 非线性方程的根通常不止一个,很难找到所有的解 非线性方程求根,通常需要给定初始值或求解范围, 用迭代法求解 (介值定理)设 是区间 上的一个连续函数, 那么 取到 与 之间的任何一个值,即如果 是 与 之间的一个数,那么存在一个数 使得 (推论) 4 f x( ) [,] a b f x( ) f a( ) f b( ) f a( ) f b( ) fc y ( ) = c ab ∈[,] f (a)⋅ f (b) < 0 ⇒ ∃x,s.t., f (x) = 0 y
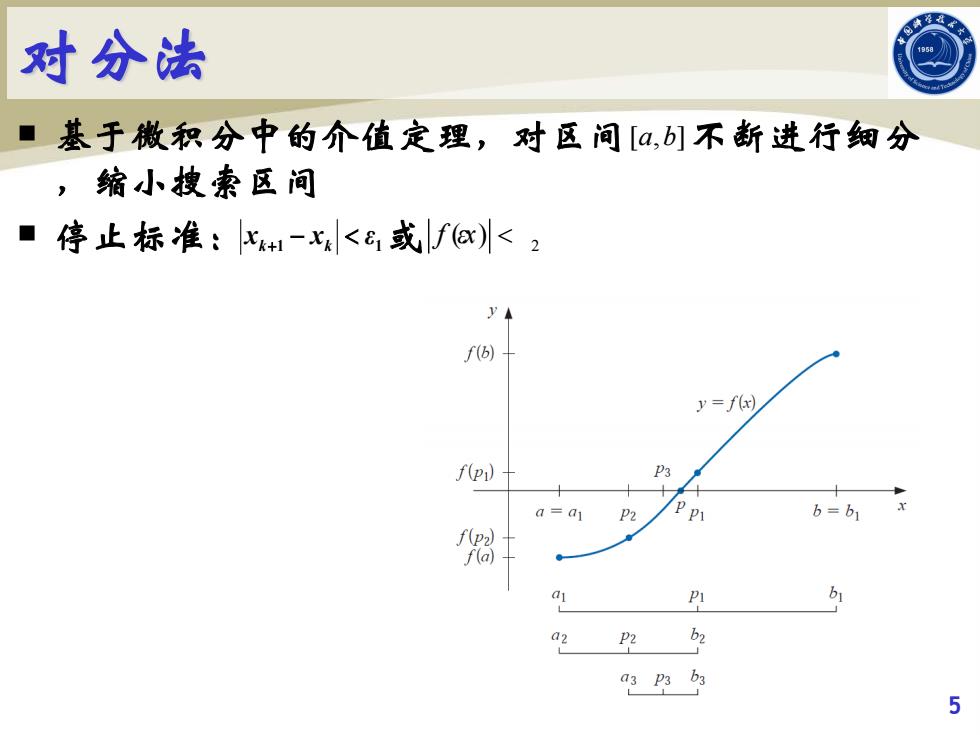
对分法 ■基于微积分中的介值定理,对区间[a,b]不断进行细分 ,缩小搜索区间 ■停止标准:x+-x<,或f<2 YA f6) y=f(x) f(pi) P3 十 a=a P2 b=b1 f(p2) f(a) 0 四 a2 P2 b2 a3 p3 b3 5
对分法 基于微积分中的介值定理,对区间 不断进行细分 ,缩小搜索区间 停止标准: 或 5 [,] a b 1 1 x x ε k+ − k < 2 f x( ) ε <
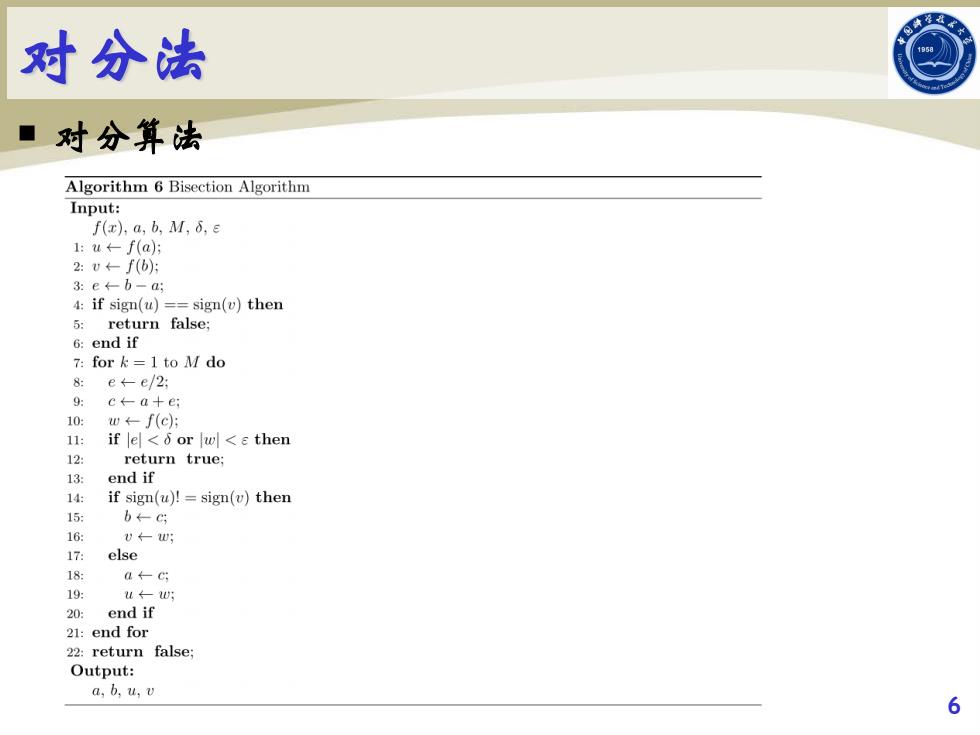
对分法 ■ 对分算法 Algorithm 6 Bisection Algorithm Input: f(x),a,b,M,6.e 1:u←-f(a: 2:v←f(b) 3:e←b-a 4:if sign(u)==sign(v)then 5:return false; 6:end if 7:for k=1 to M do 8:e-e/2: 9:c←-a+eg 10:w←f(c: 11: if e<6 or w<then 12: return true; 13: end if 14: if sign(u)!sign(v)then 15: b←- 16: U←-U; 17: else 18: a←-c 19: u← 20:end if 21:end for 22:return false; Output: a,b,u,v 6
对分法 对分算法 6