
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第4章非线性方程求根 非线性科学是当今科学发展的一个重要研究方向,而非线性 方程的求根也成了一个不可缺的内容。但是,非线性方程的求根 非常复杂。 通常非线性方程的根的情况非常复杂: a=1 无解 sin( a= 一个解 无穷组解 Jy=x2+a 4 lx=y2+a a=0 两个解 y= a=-1 四个解
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第4章 非线性方程求根 非线性科学是当今科学发展的一个重要研究方向,而非线性 方程的求根也成了一个不可缺的内容。但是,非线性方程的求根 非常复杂。 通常非线性方程的根的情况非常复杂: = = 2 1 ) 2 sin( y x y 无穷组解 = − = = = = + = + 1 0 4 1 1 2 2 a a a a x y a y x a 无解 一个解 两个解 四个解

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 所以,只在某个区域内可能解存在唯一,而且经常很简单的 形式得不到精确解: e*-1=cos(x) 因此,通常我们用迭代法解非线性方程 看迭代法之前,先看看一种简单直观的方法 原理:f(a)f(b)<0→3x,s.t,f(x)=0
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 所以,只在某个区域内可能解存在唯一,而且经常很简单的 形式得不到精确解: 因此,通常我们用迭代法解非线性方程 看迭代法之前,先看看一种简单直观的方法 原理: f (a) f (b) 0 x,s.t., f (x) = 0 e 1 cos( x) x − =
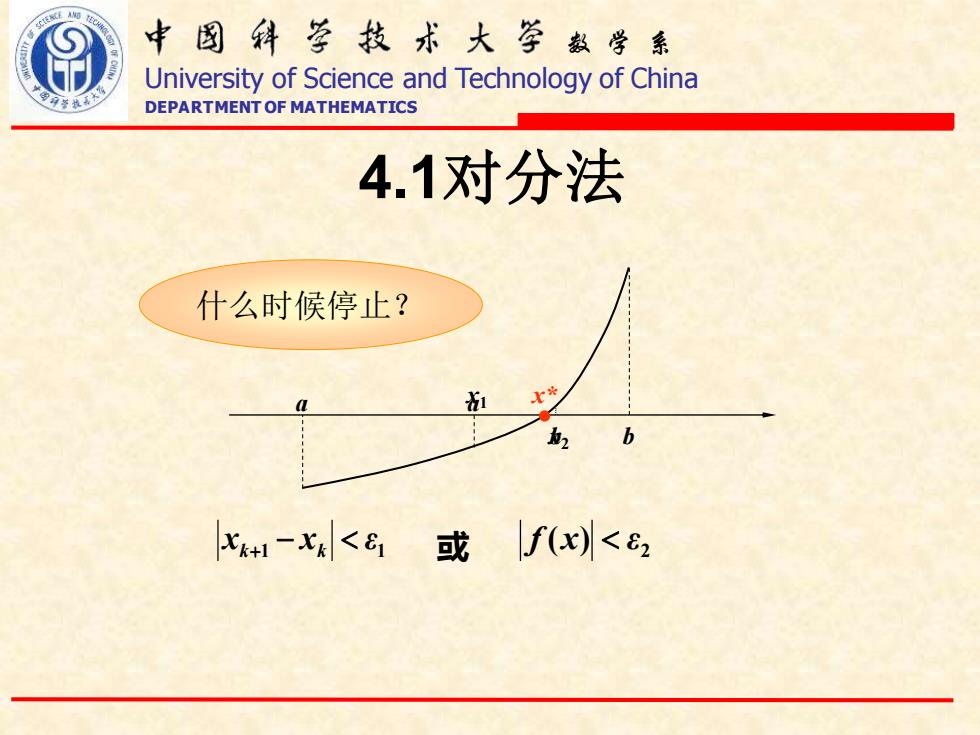
中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 4.1对分法 什么时候停止? 缸 x 2 x+-<或f(x)<2
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 4.1对分法 a b x1 x2 a b 什么时候停止? 1 1 x x ε k+ − k 2 或 f (x) ε x*

中图 科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 算法 While(la-bl>eps) x=(a+b)/2 fx刈 若(Ifx<eps)x为解 若f*fb)<0修正区间为x,b 若f(a)*fx<0修正区间为a,刈 End while 每次缩小一倍的区间,收敛速度为1/2,较慢,且只能求 一个根,使用条件限制较大 不能保证x的精度
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS While(|a-b|>eps) x=(a+b)/2 f(x) 若(|f(x)|<eps) x为解 若f(x)*f(b)<0 修正区间为[x,b] 若f(a)*f(x)<0 修正区间为[a,x] End while 每次缩小一倍的区间,收敛速度为1/2,较慢,且只能求 一个根,使用条件限制较大 算法 2 x* x 不能保证 x 的精度

中图科堂技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 4.2迭代法 等价变换 fx)=0 x=g(x) f(x)的根 g(心)的不动点 从一个初值x出发,计算x1=go),x2=gc1), 思 x+1=g化,.若{x收敛,即存在*使得 路 mxk=x*,且g连续,则由mxk+1=阿( gc*),即x*是g的不动点,也就是f的根
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 4.2 迭代法 f (x) = 0 x = g (x) 等价变换 f (x) 的根 g (x) 的不动点 思 路 从一个初值 x0 出发,计算 x1 = g(x0 ), x2 = g(x1 ), ., xk+1 = g(xk ), . 若 收敛,即存在 x* 使得 ,且 g 连续,则由 可知 x* = g(x* ),即x* 是 g 的不动点,也就是f 的根。 k k=0 x lim x x * k k = → ( ) k k k k x g x → + → lim 1 = lim