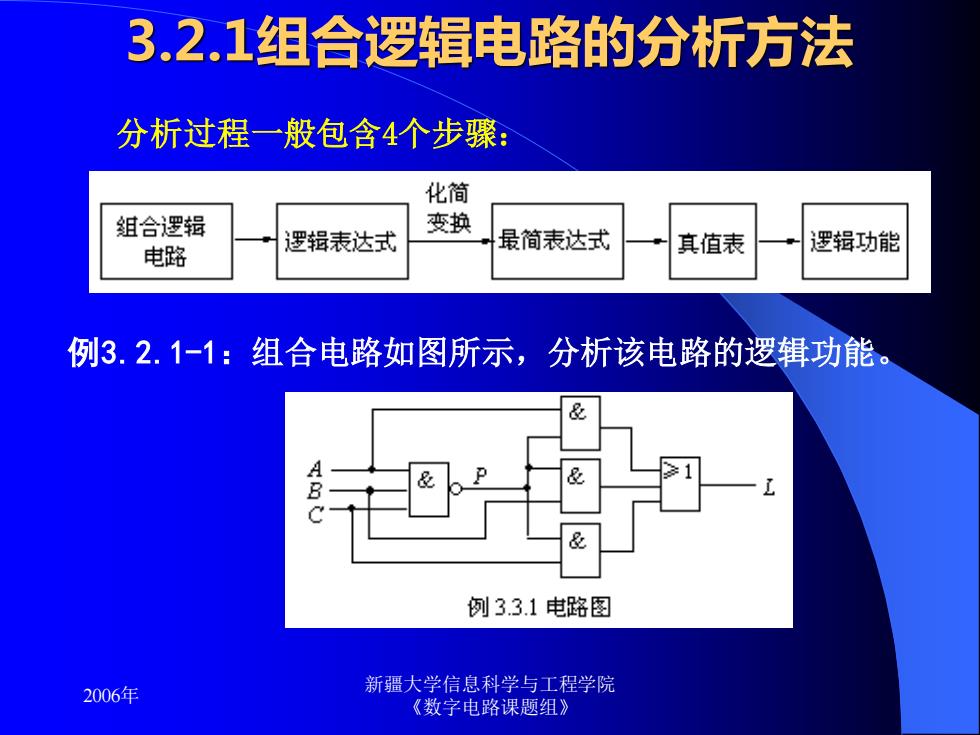
3.2.1组合逻辑电路的分析方法 分析过程一般包含4个步骤: 化简 组合逻辑 变换 逻辑表达式 最简表达式 真值表 逻辑功能 电路 例3.2.1-1:组合电路如图所示, 分析该电路的逻辑功能。 例3.3.1电路图 2006年 新疆大学信息科学与工程学院 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 3.2.1组合逻辑电路的分析方法 分析过程一般包含4个步骤: 例3.2.1-1:组合电路如图所示,分析该电路的逻辑功能
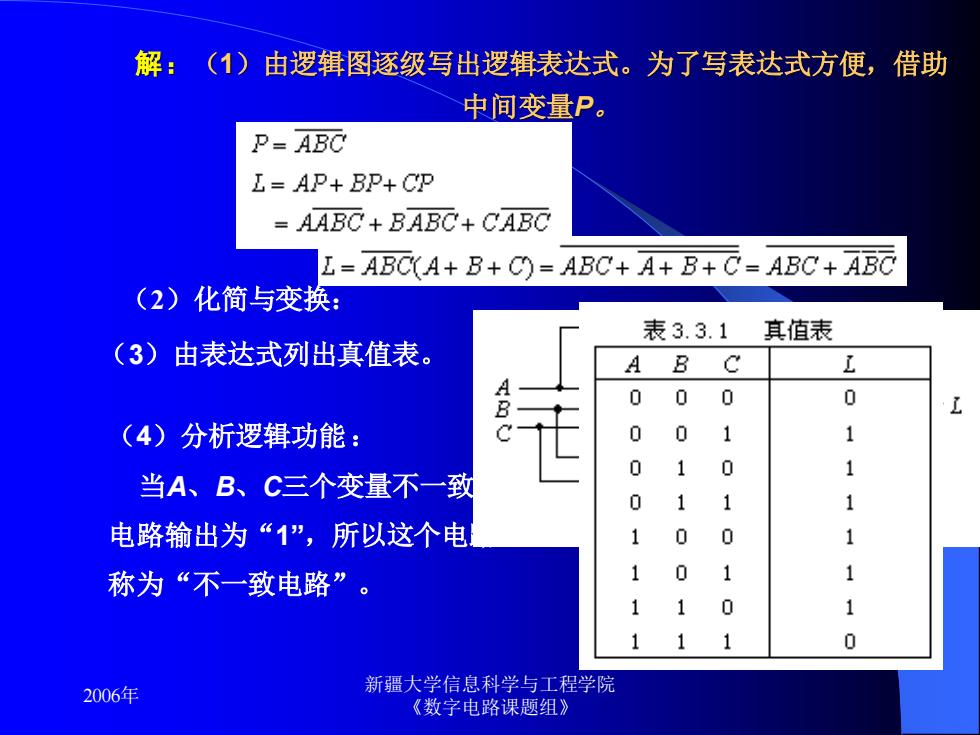
解:(1) 由逻辑图逐级写出逻辑表达式。为了写表达式方便,借助 中间变量P。 P=ABC L=AP+BP+CP AABC+BABC+CABC L=ABC(A+B+C=ABC+A+B+C=ABC+ABC (2) 化简与变换: 表3.3.1 真值表 (3)由表达式列出真值表。 C L AB 0 0 0 0 (4)分析逻辑功能: 0 0 1 1 0 1 0 1 当A、B、C三个变量不一致 1 1 1 电路输出为“1”,所以这个电 1 0 0 1 称为“不一致电路”。 1 1 1 11 0 1 1 1 0 2006年 新疆大学信息科学与工程学院 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 解:(1)由逻辑图逐级写出逻辑表达式。为了写表达式方便,借助 中间变量P。 (2)化简与变换: (3)由表达式列出真值表。 (4)分析逻辑功能: 当A、B、C三个变量不一致时, 电路输出为“1” ,所以这个电路 称为“不一致电路”
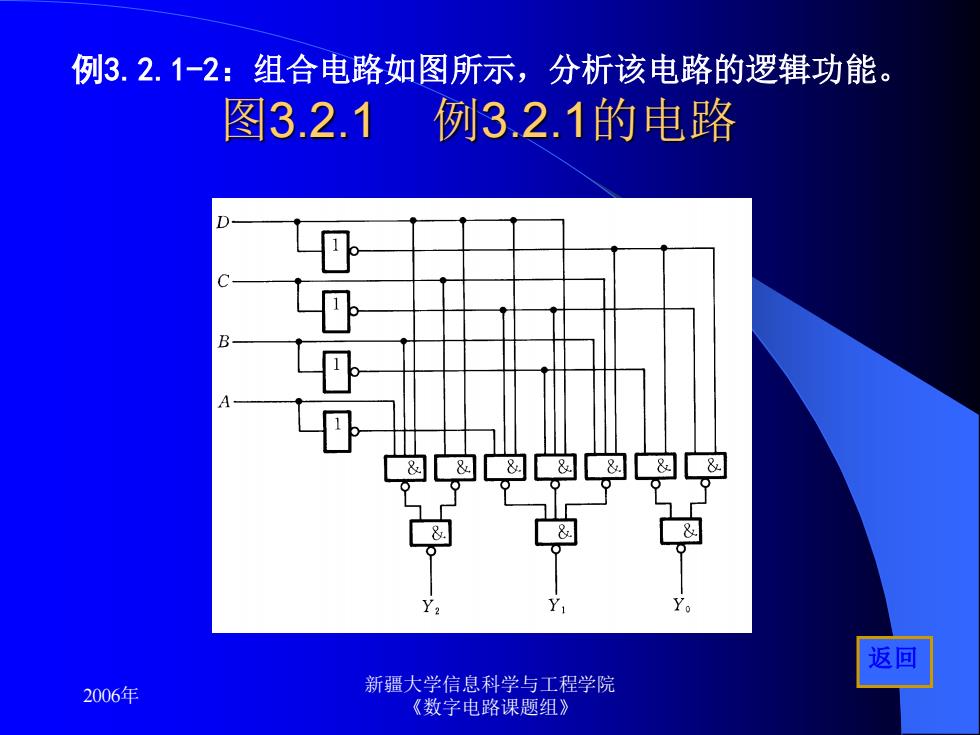
例3.2.1-2:组合电路如图所示,分析该电路的逻辑功能。 图3.2.1 例3.2.1的电路 B A &购a☒☒8 8 Y。 返回 2006年 新疆大学信息科学与工程学院 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 例3.2.1-2:组合电路如图所示,分析该电路的逻辑功能。 图3.2.1 例3.2.1的电路 返回

例3.2.1-2:组合电路如图所示,分析该电路的逻辑功能。 解: 根据给出的逻辑图可写出Y2、Y1、Y。和D、C、B、A之间的逻辑函数式 Y2=DC·DBA=DC+DBA Y,=DCB·DOB·DCA=DCB+DCB+DCA Y。=DC·DB=DC+B 从上面的逻辑函数式中我们还不能立刻看出这个电路的逻辑功能和用 为此,还需将式(3.2.1)转换成真值表的形式,得到表3.2.1。 1,腰 表3.2.1图3.2.1电路的逻辑真值表 人 输 图 D B Y2 YI D 0 0 0 01 0 0 0 0 0 0 0 1 0 0 0 0 》 0 10 0 0 1 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 0 2006年 新疆大学信息科学与工程学院 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 例3.2.1-2:组合电路如图所示,分析该电路的逻辑功能。 返回

3.2.2组合逻辑电路的设计方法 与分析过程相反,组合逻辑电路的设计是根据给 定的实际逻辑问题,求出实现其逻辑功能的最简单的 逻辑电路。 1.组合逻辑电路的大致设计步骤: (1)分析设计要求,设置输入输出变量并逻辑赋值; (2)列真值表; (3)写出逻辑表达式,并化简; (4)画逻辑电路图。 2006年 新疆大学信息科学与工程学院 《数字电路课题组》
2006年 新疆大学信息科学与工程学院 《数字电路课题组》 3.2.2 组合逻辑电路的设计方法 1.组合逻辑电路的大致设计步骤: (1)分析设计要求,设置输入输出变量并逻辑赋值; (2)列真值表; (3)写出逻辑表达式,并化简; (4)画逻辑电路图。 与分析过程相反,组合逻辑电路的设计是根据给 定的实际逻辑问题,求出实现其逻辑功能的最简单的 逻辑电路