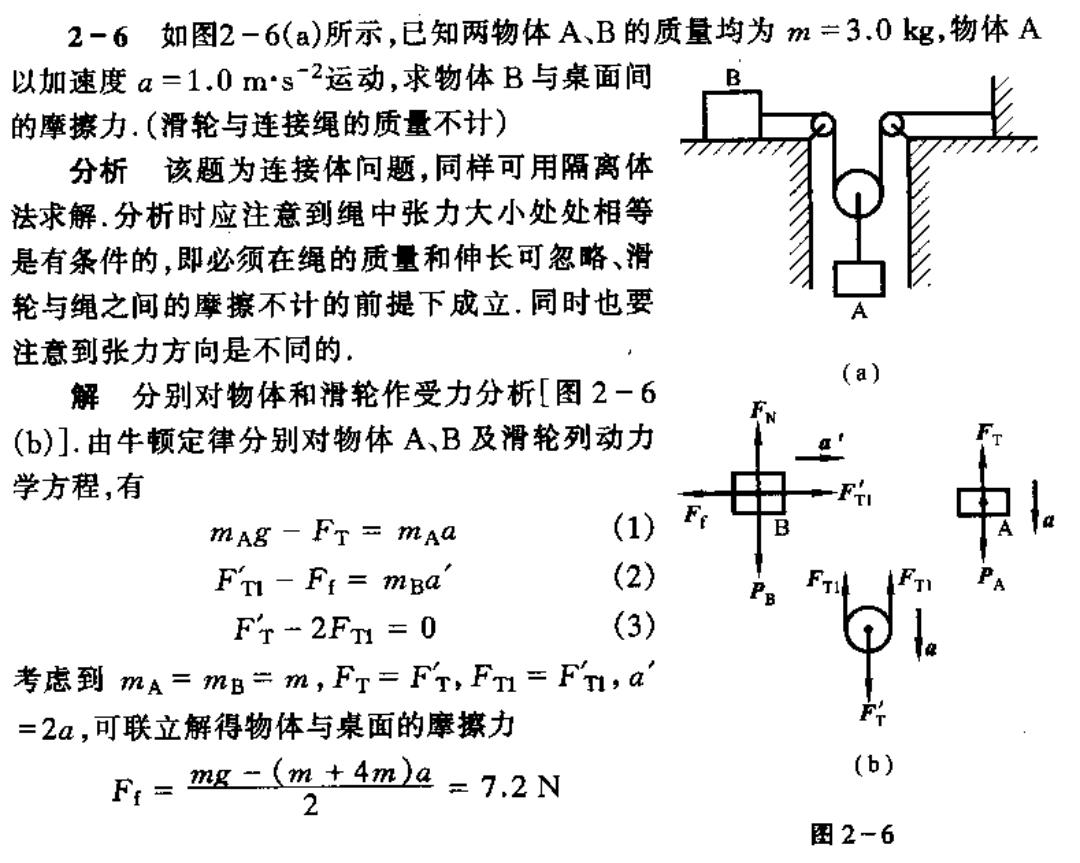
2-6如图2-6(a)所示,已知两物体A、B的质量均为m=3.0kg,物体A 以加速度a=1.0ms2运动,求物体B与桌面间 的摩擦力.(滑轮与连接绳的质量不计) 分析该题为连接体问题,同样可用隔离体 法求解.分析时应注意到绳中张力大小处处相等 是有条件的,即必须在绳的质量和伸长可忽略、滑 轮与绳之间的摩擦不计的前提下成立.同时也要 注意到张力方向是不同的。 解分别对物体和滑轮作受力分析[图2-6 (b)门.由牛顿定律分别对物体A、B及滑轮列动力 学方程,有 mAg -FT mAa (1) FTI-Fi=mBa' (2) F'T-2FTI =0 (3) 考虑到mA=mB=m,FT=F,FT=F,a =2a,可联立解得物体与桌面的摩擦力 F=mg-(m+4m=7,2N 2-6

2-7质量为m的长平板A以速度在光滑平面上作直线运动,现将质 量为m的木块B轻轻平稳地放在长平板上,板与木块之间的动摩擦因数为4, 求木块在长平板上滑行多远才能与板取得 B 共同速度? 分析当木块B平稳地轻轻放至运动 着的平板A上时,木块的初速度可视为零】 由于它与平板之间速度的差异而存在滑动 图2-7 摩擦力,该力将改变它们的运动状态.根据牛顿定律可得到它们各自相对地面的 加速度.换以平板为参考系来分析,此时,木块以初速度-。(与平板运动速率大 小相等、方向相反)作匀诚速运动,其加速度为相对加速度,按运动学公式即可 解得 该题也可应用第三章所讲述的系统的动能定理来解.将平板与木块作为系 统,该系统的动能由平板原有的动能变为木块和平板一起运动的动能,而它们的 共同速度可根据动量定理求得,又因为系统内只有摩擦力做功,根据系统的动能 定理,摩擦力的功应等于系统动能的增量.木块相对平板移动的距离即可求出. 解1以地面为参考系,在摩擦力F:=4g的作用下,根据牛顿定律分别 对木块、平板列出动力学方程 Fr=umg ma Fi=-Fr=m'a2 a1和a2分别是木块和木板相对地面参考系的加速度.若以木板为参考系,木块 相对平板的加速度a=a1+a2,木块相对平板以初速度-。作匀减速运动直至 最终停止.由运动学规律有 u'2=2a9 由上述各式可得木块相对于平板所移动的距离为 5=2g(m+m】 解2以木块和平板为系统,它们之间一对摩擦力的功为 W=Fi(s +1)-Fil umgs 式中1为平板相对地面移动的距离. 由于系统在水平方向上不受外力,当木块放至平板上时,根据动量守恒定 律,有 mv=(m+m) 由系统的动能定理,有 gmgs =mv2(m+m)v2 由上述各式可得 m'v2 s=2g(m+m】