
6.1定积分的概念及性质 二.定积分的定义 定义设f(x)是定义在[a,b]上的有界函数,任取一组 分点:=0<X1<X2<<Xi-1<Xi<<xm-1<xn=b, 把[a,b]分成n个小区间[xi-1,x(i=l,2,.n), ix-1,xi,作和式∑f(5)Ax,其中△=xi-x-1, i=1 令d=max {△}, 当d→0时,和式的极限存在, l≤i≤n 且与[α,b及5取法无关,则称此极限为函数 f)在a,b1上的定积分,记作∫fx)dc,即
6.1 定积分的概念及性质 定义 设 f (x) 是定义在[a, b]上的有界函数,任取一组 分点: [ , ], i xi−1 xi , a=x0 x1 x2 xi−1 xi xn−1 xn =b 把[a, b]分成 n 个小区间[ , ] i 1 i x x − ( i=1, 2, n ), max , 1 i i n d = x 令 ( ) , , 1 1 − = i = i − i n i 作和式 f i xi 其 中 x x x 二. 定积分的定义 且 与 [a,b] 及 i 取 法 无 关 , 则 称 此 极 限 为 函 数 f (x)在[a,b]上的定积分,记作 b a f (x)dx ,即 当d → 0 时,和式的极限存在
6.1定积分的概念及性质 积分上限 积分和 lim ∑f(5)△;. d→0 积分下限 被积函数 被积表达式 积分变量 [a,b]积分区间 若定积分∫fv)dr存在,则称f)在[a,1上可积 定积分就是特殊和式的极限
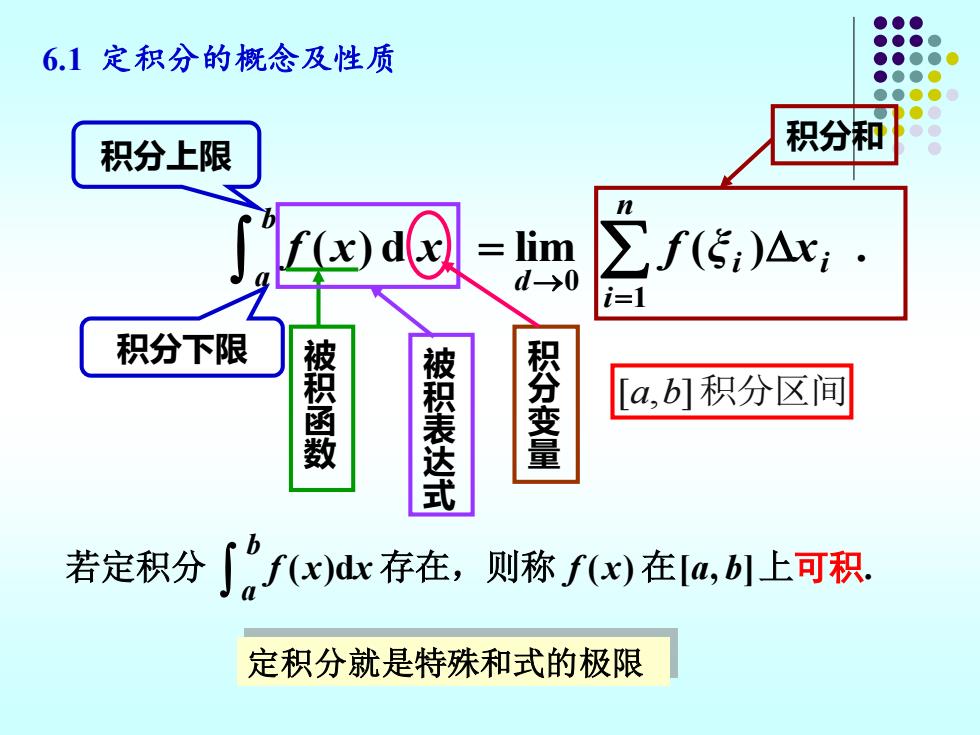
6.1 定积分的概念及性质 ( ) d lim ( ) . 1 0 = → = n i i i d b a f x x f ξ x 被 积 函 数 被 积 表 达 式 [ , ] a b 积分区间 积分上限 积分下限 积 分 变 量 积分和 若定积分 b a f (x)dx 存在,则称 f (x) 在[a, b]上可积. 定积分就是特殊和式的极限