
例:蒲丰投针(1777) 6 在平面上有等距离的平行线,平行线间的距离 为2a(a>0),在该平面任意投掷一枚长为2l (L<α)的针,求该针与任一平行线相交的概率
例:蒲丰投针(1777) 在平面上有等距离的平行线,平行线间的距离 为𝟐𝒂 (𝒂 > 𝟎),在该平面任意投掷一枚长为𝟐𝒍 (𝒍 < 𝒂)的针,求该针与任一平行线相交的概率. 6
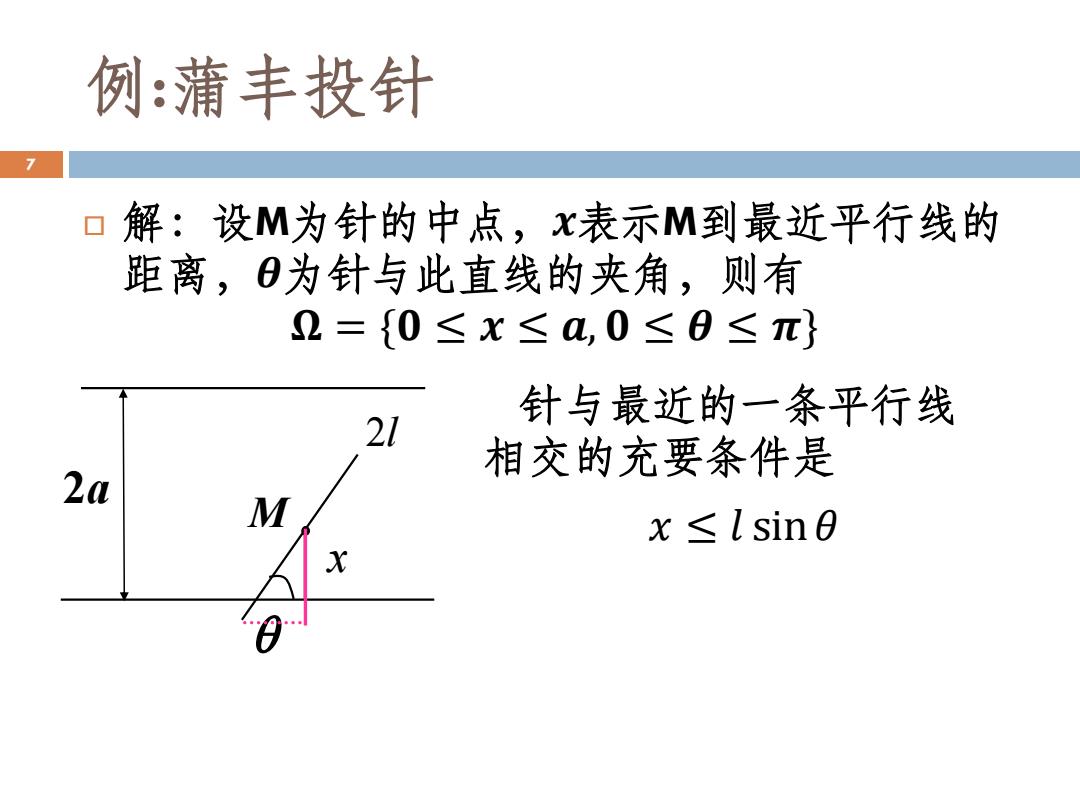
例:蒲丰投针 0 解:设M为针的中点,x表示M到最近平行线的 距离,0为针与此直线的夹角,则有 2={0≤X≤a,0≤0≤π} 21 针与最近的一条平行线 相交的充要条件是 20 M x≤lsin0 X
例:蒲丰投针 解:设M为针的中点,𝒙表示M到最近平行线的 距离,𝜽为针与此直线的夹角,则有 𝛀 = {𝟎 ≤ 𝒙 ≤ 𝒂, 𝟎 ≤ 𝜽 ≤ 𝝅} 7 • 2a x M 2l 针与最近的一条平行线 相交的充要条件是 𝑥 ≤ 𝑙 sin𝜃
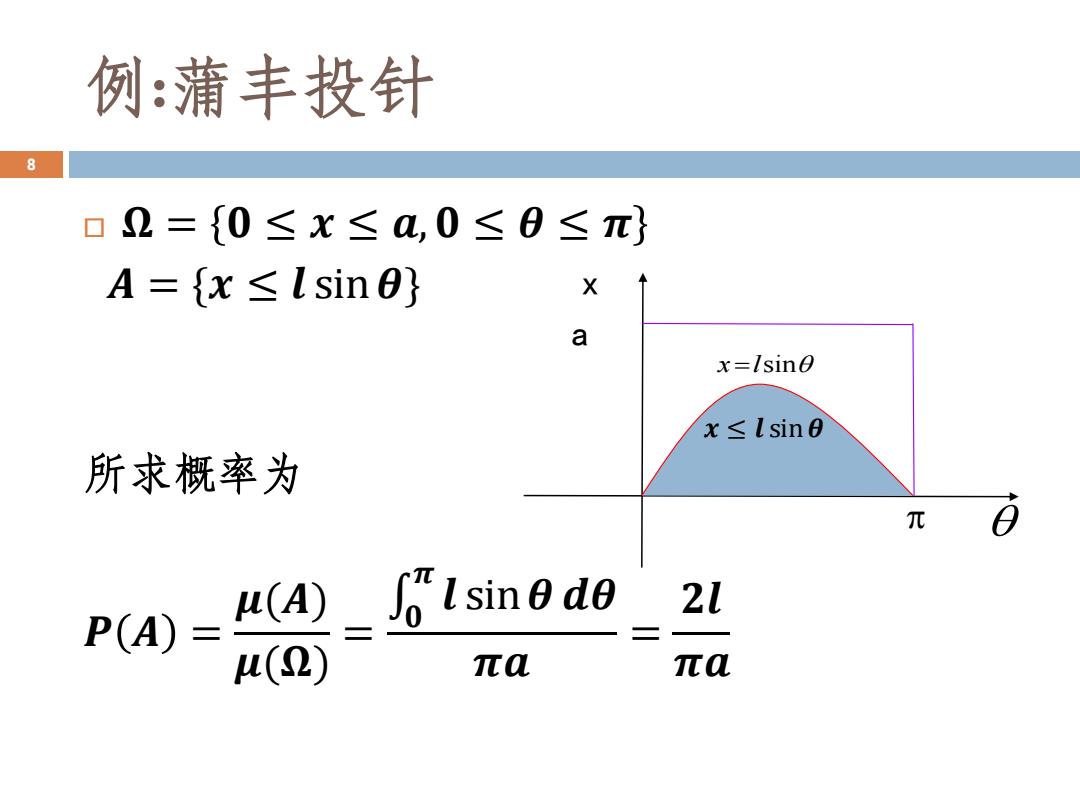
例:蒲丰投针 8 口2={0≤x≤a,0≤0≤π} A={x≤Isin0} a x=Isin0 x≤lsinθ 所求概率为 元 P(A)= (A) Isinede 21 二 u(2) πa 元
例:蒲丰投针 𝛀 = 𝟎 ≤ 𝒙 ≤ 𝒂, 𝟎 ≤ 𝜽 ≤ 𝝅 𝑨 = {𝒙 ≤ 𝒍 sin𝜽} 所求概率为 𝑷 𝑨 = 𝝁(𝑨) 𝝁(𝛀) = �� 𝝅 𝒍 sin𝜽 𝒅𝜽 𝝅𝒂 = 𝟐𝒍 𝝅𝒂 8 x a x l = sin 𝒙 ≤ 𝒍 sin𝜽

例:蒲丰投针 9 如果l和a已知,则以π值代入上式可以求出p= P(A). ▣反之,可用上式求π的近似值:以试验频率近似 概率。 ▣投针N次,其中针与平行线相交n次,以频率n/N 作为概率卫的近似值,代入上式有: 2IN π≈ an
例:蒲丰投针 如果𝒍和𝒂已知,则以𝝅值代入上式可以求出𝒑 = 𝑷 𝑨 . 反之,可用上式求𝝅的近似值:以试验频率近似 概率。 投针N次,其中针与平行线相交𝒏次,以频率𝒏/𝑵 作为概率𝒑的近似值,代入上式有: 𝝅 ≈ 𝟐𝒍𝑵 𝒂𝒏 9
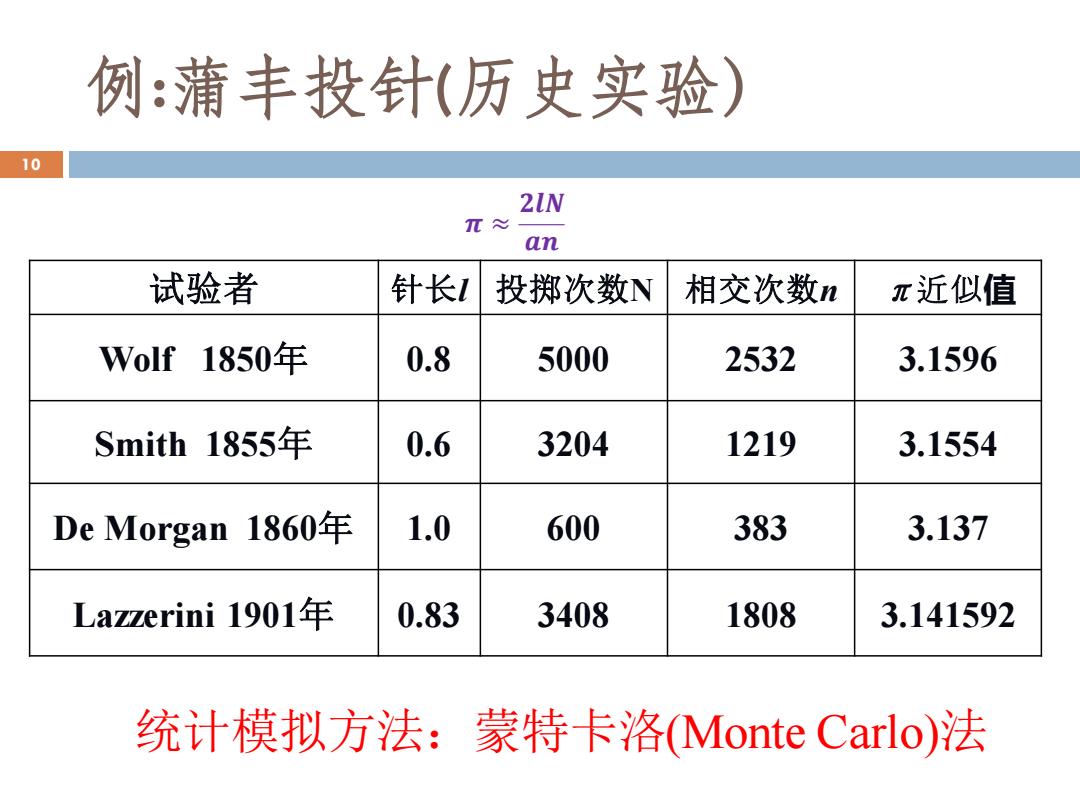
例:蒲丰投针(历史实验) 10 2IN π≈ an 试验者 针长L 投掷次数N 相交次数n π近似值 Wolf1850年 0.8 5000 2532 3.1596 Smith1855年 0.6 3204 1219 3.1554 De Morgan1860年 1.0 600 383 3.137 Lazzerini1901年 0.83 3408 1808 3.141592 统计模拟方法:蒙特卡洛(Monte Carlo)法
例:蒲丰投针(历史实验) 10 𝝅 ≈ 𝟐𝒍𝑵 𝒂𝒏 试验者 针长l 投掷次数N 相交次数n π近似值 Wolf 1850年 0.8 5000 2532 3.1596 Smith 1855年 0.6 3204 1219 3.1554 De Morgan 1860年 1.0 600 383 3.137 Lazzerini 1901年 0.83 3408 1808 3.141592 统计模拟方法:蒙特卡洛(Monte Carlo)法