《电磁场与电磁能》课程PPT教学课件（杨儒贵版）第八章 平面电磁波

麦克斯韦方程静态场中的高斯定理及磁通连续性原理对于时变电磁场仍然成立。那么，对于时变电磁场，麦克斯韦归纳为四个方程，其积分形式和微分形式分别如下：积分形式微分形式aDaD全电流定律H.dL-.dsVxH=J+atataBaB电磁感应定律E.dl:.dsVxE=atat磁通连续性原理Φ. B.ds=0V.B=0厂高斯定律, D.dS=qV.D=papV.J=D=&EB=μHJ=oE+J'at

麦克斯韦方程 静态场中的高斯定理及磁通连续性原理对于时变电磁 场仍然成立。那么，对于时变电磁场，麦克斯韦归纳为 四个方程，其积分形式和微分形式分别如下： d ( ) d l S t   = +     D H l J S d d l S t   = −     B E l S d 0 S  =  B S d S  = q  D S 积分形式 t   = + D H J t    = − B E B = 0   D =  微分形式 全电流定律 电磁感应定律 磁通连续性原理 高斯定律 t    = −  J D =  E B =  H J = E + J

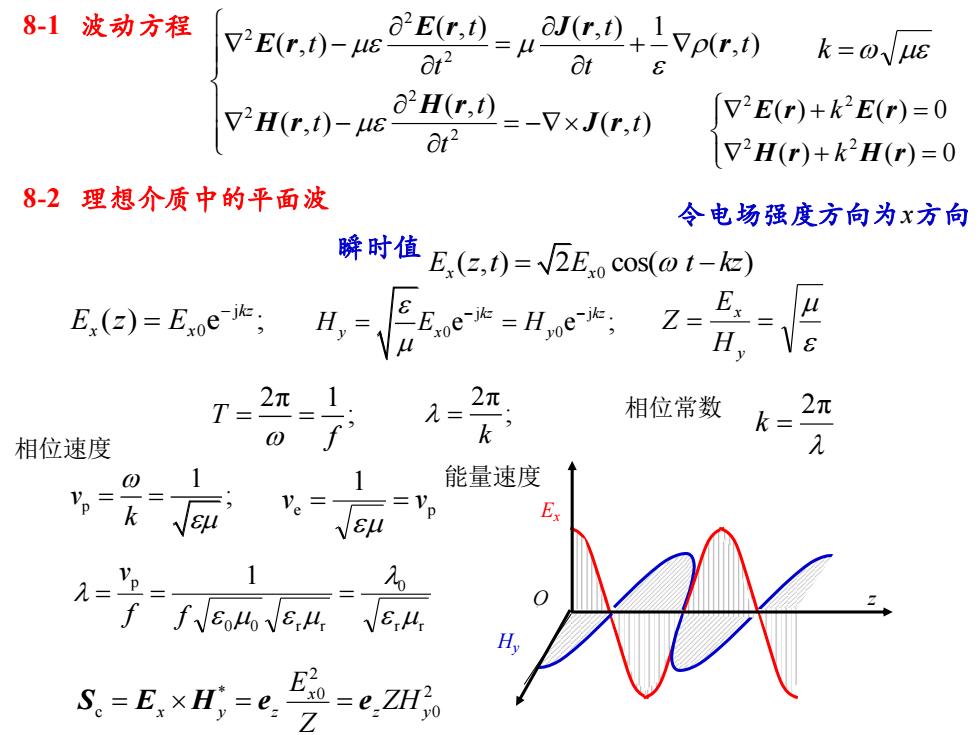
8-1 波动方程αE(r,t)aJ(r,t)1?E(r,t)--Vp(r,t)k=のyueL18at?at8o°H(r,t)?E(r)+k?E(r)= 0V"H(r,t)-μeVxJ(r,t)at?V?H(r)+kH(r) = 08-2理想介质中的平面波令电场强度方向为x方向瞬时值 E,(z,t)= /2Exo cos(α t-ke)DEμ0E(z) = Exoe-jks;H.E.H,N8u2元2元12元相位常数T :1=k0元相位速度1能量速度10VpVe2RExkJeuVsu12V.20fcoeuVeH,E2oe.ZH?S =E xHvoZ

8-2 理想介质中的平面波 8-1 波动方程        = −    − +    =    − ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) 1 ( , ) 2 2 2 2 2 2 t t t t t t t t t t J r H r H r r E r J r E r           + =  + = ( ) ( ) 0 ( ) ( ) 0 2 2 2 2 H r H r E r E r k k 令电场强度方向为x方向 瞬时值 0 ( , ) 2 cos( ) E z t E t kz x x = −  j 0 ( ) e ; kz E z E x x − = 2π 1 T ;  f = = 2π ; k  =  2π k = p 1 v ; k   = = r r 0 0 0 r r p 1         = = = f f v   = = y x H E Z 2 0 2 * 0 c z y x x y z ZH Z E S = E  H = e = e e p 1 v = = v  j j 0 0 e e ; kz kz H E H y x y   − − = = O z Hy Ex 相位常数 能量速度 相位速度 k = 

E,(z,t)= ~2Ero cos(o t-kz)均匀平面波k=のuskz时间相位：のt空间相位：波面空间相位相等的点组成的曲面称为2元_1T:时间相位のt变化2元所经历的时间。周期（T）)f0一秒内相位变化2元的次数。频率 ()元=2元空间相位kz变化2元所经过的距离。波长 ()k相位常数k表示单位长度内的相位变化。又称为波数2元k=dz_0元相位速度VVpdtk根据相位不变点的轨迹变化可以计算电磁波的相位变化速度，Eu这种相位速度以v表示@ t-kz = const7波阻抗电场强度与磁场强度之，以Z表示H,V&横电磁波，TEM波对于传播方向而言，电场及磁场仅具有横向分量Sav1能量速度2=VpV.WavVeu

均匀平面波 0 ( , ) 2 cos( ) E z t E t kz x x = −  时间相位:  t 空间相位: kz 波面 空间相位相等的点组成的曲面称为 周期（T ） 时间相位 t 变化 2 所经历的时间。 f T 2π 1 = =  频率（f ） 一秒内相位变化2 的次数。 波长（ ） 空间相位kz 变化 2 所经过的距离。 k 2π  = 相位常数 k 表示单位长度内的相位变化。又称为波数  2π k = 相位速度vp t k z v  = = d d p 波阻抗 电场强度与磁场强度之，以Z 表示   = = y x H E Z 横电磁波，TEM波 对于传播方向而言，电场及磁场仅具有横向分量 能量速度 av av e w S v = e p 1 v = = v  k =  根据相位不变点的轨迹变化可以计算电磁波的相位变化速度， 这种相位速度以 vp 表示  const t kz − =

缩波效应已知平面波的频率是由波源决定的，但是平面波的相速与介质特性有关。因此，平面波的波长与介质特性有关。1由上求得2=p+fcooVerurVou01式中MokfJeoo孔o是频率为f的平面波在真空中传播时的波长。可见，几<几。。这种现象称为波长缩短效应或缩波效应。折射率：光在真空中的速度与光在该材料中的速度之比率

已知平面波的频率是由波源决定的，但是平面波的相速与介质 特性有关。因此，平面波的波长与介质特性有关。 r r 0 0 0 r r p 1         = = = f f 由上求得 v 式中 0 0 0 1    f = 0 是频率为f 的平面波在真空中传播时的波长。 可见， 。这种现象称为波长缩短效应或缩波效应。   0 缩波效应 p 1 v ; k   = = 折射率：光在真空中的速度与光在该材料中的速度之比率

色散(()+)'=08-3.导电介质中的平面波电场强度可写为k=0/[/()-1E,=Eroe-jk==Ere-k"e-jks式中第一个指数表示电场强度的振幅随2增加不断衰减，第二个指数表示相位变化。因此，k称为相位常数，单位为rad/m；k"称为衰减常数，单位为Np/m，而k.称为传播常数。0导电介质中的相速为k可见，相速不仅与介质参数有关，还与频率有关各个频率分量的电磁波以不同的相速传播，经过一段距离后各个频率分量之间的相位关系将发生变化，导致信号失真，这种现象称为色散。所以导电质又称为色散媒质

k z k z x k z Ex Ex E − −  −  = = j 0 j 0 e e e c 电场强度可写为 式中第一个指数表示电场强度的振幅随z 增加不断衰减，第二个指 数表示相位变化。因此，k 称为相位常数，单位为rad/m；k 称为 衰减常数，单位为Np/m，而kc 称为传播常数。 导电介质中的相速为          +      + =   = 1 1 2 1 2 p     k v 可见，相速不仅与介质参数有关，还与频率有关。 各个频率分量的电磁波以不同的相速传播，经过一段距离后， 各个频率分量之间的相位关系将发生变化，导致信号失真，这种 现象称为色散。所以导电质又称为色散媒质。 8-3. 导电介质中的平面波 色散 1 1 2 2          +       = +    k  1 1 2 2          −       = +    k 