《电磁场与电磁能》课程PPT教学课件（杨儒贵版）第五章 恒定磁场

I2di,×(I,di, ×ar)μo.、安培力定律 dR24元Ho f idi ,xar二、比奥一—沙伐定律B,=R24元C2J(x',y,z)xarHoB(x,y,z) =R?4元VHo [j(t',y',z)xar ds"B(x,y,z)R24元s三、安培力F21=12dl,×BOF=F+F=q(vxB+E)四、洛仑兹办qv×B=q(i×B)

一、安培力定律 二、比奥——沙伐定律 B1= 四、洛仑兹力 三、安培力

五、磁感应强度的散度B（）=>R4元V.(V× F)= 0则 .B=0六、磁感应强度的通量Φm=「B.dS七、磁通连续性原理$B.ds = 0S

五、磁感应强度的散度              dV R J r B r V ( ) 4 ( ) 0       B 0 F           则 ( ) 0 七、磁通连续性原理 六、磁感应强度的通量     s m B dS     0 S B dS  

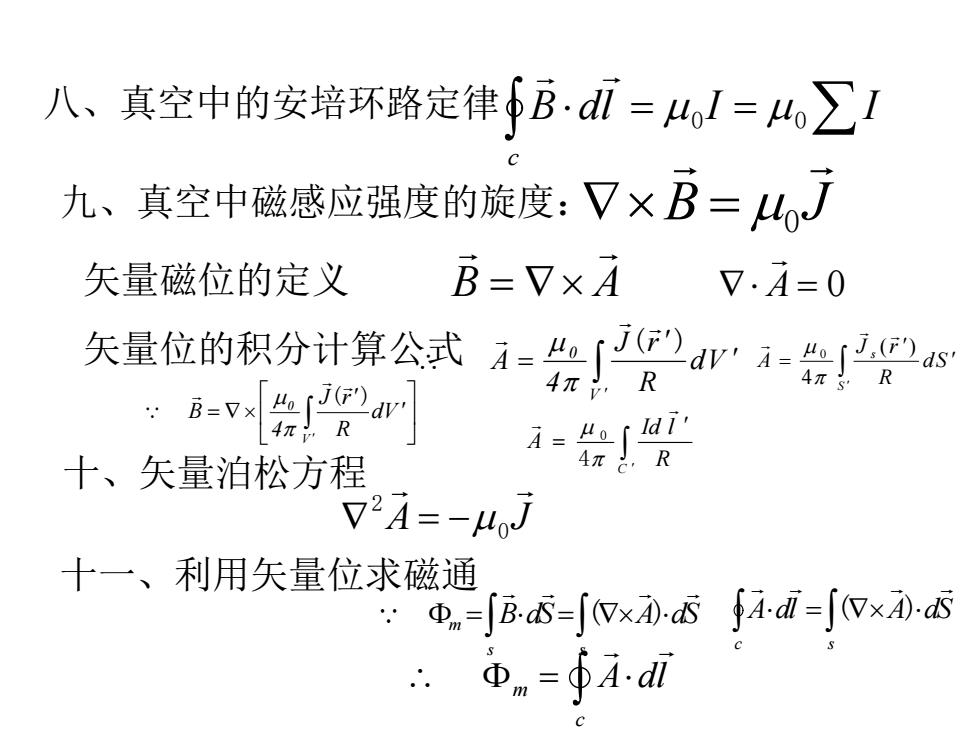
八、真空中的安培环路定律Bdi=o=I九、真空中磁感应强度的旋度：×B=uoB=V×A矢量磁位的定义V.A=0j(r)失量位的积分计算公式4=o0.2as4=dy4元RR4元／B=[[(avIdi'R4元：4oA=R4元十、矢量泊松方程V?A=-μoJ十一、利用矢量位求磁通+A-di -[(V×A)-dS @m={B.dS-{(VxA)-dsbA.dlΦ.一12

矢量位的积分计算公式  A  0  B   A   矢量磁位的定义 九、真空中磁感应强度的旋度： B J     0 八、真空中的安培环路定律 B dl  I  I c 0 0   A dl A dS c s          ( ) m c    A dl     十一、利用矢量位求磁通 A J   0 2    十、矢量泊松方程             V  0 dV R J r 4 B ( )            S s dS R J r A ( ) 4 0          C R Id l A     4 0       V 0 dV R J r 4 A ( )      B dS A dS s s m             ( )

磁矩Pm=IS十二、媒质的磁极子抗磁性媒质顺磁性媒质铁磁性媒质Zpm磁化强度M：M = limA/mAVAV->0A(F)=[xMMxi dsA(F)=HoPm ×RuodJ..=VxM4元R3RR4元4元Sj=MxnA()=av+ds4元R4元／R1：磁化体电流密度（束缚体电流）；1磁化面电流密度（束缚面电流）

十二、媒质的磁磁化偶: 极子 磁矩 抗磁性媒质 顺磁性媒质 铁磁性媒质 磁化强度 M ：  A/m V p M m V O        lim p m IS    dS R J dV R J A r S sm V m                 4 4 ( ) 0 0 ： 磁化体电流密度（束缚体电流）； sm ： 磁化面电流密度（束缚面电流）。 m J J   dS R M n dV R M A r V S                    4 4 ( ) 0 0 J M n J M sm m          3 0 4 ( ) R p R A r m       

H导磁媒质中的安培环路定律：B-di = μo(I+ I.) Im=Jmds-[(M)s =fM.diP(E-M).di = IF=(B磁场强度：A/m-M)uoo微分形式：VxH-J线性、各向同性媒质中，B.H.M之间的关系：M=xmHXm：磁化率B=(H+M)=%(+xm)HB= Hou,H =μHμr：相对磁导率

导磁媒质中的安培环路定律: ( ) 0 m c B  d l  I  I            s s m m I J dS M dS     ( )    c M dl   M dl I B c        ( )  0 ( ) 0 M B H       H d l I c      磁场强度：A/m 微分形式： H J     线性、各向同性媒质中，B H M 之间的关系：    . . M  mH  m    ：磁化率 B r H H      0   B H M m H     0(  )0(1 )  r ：相对磁导率