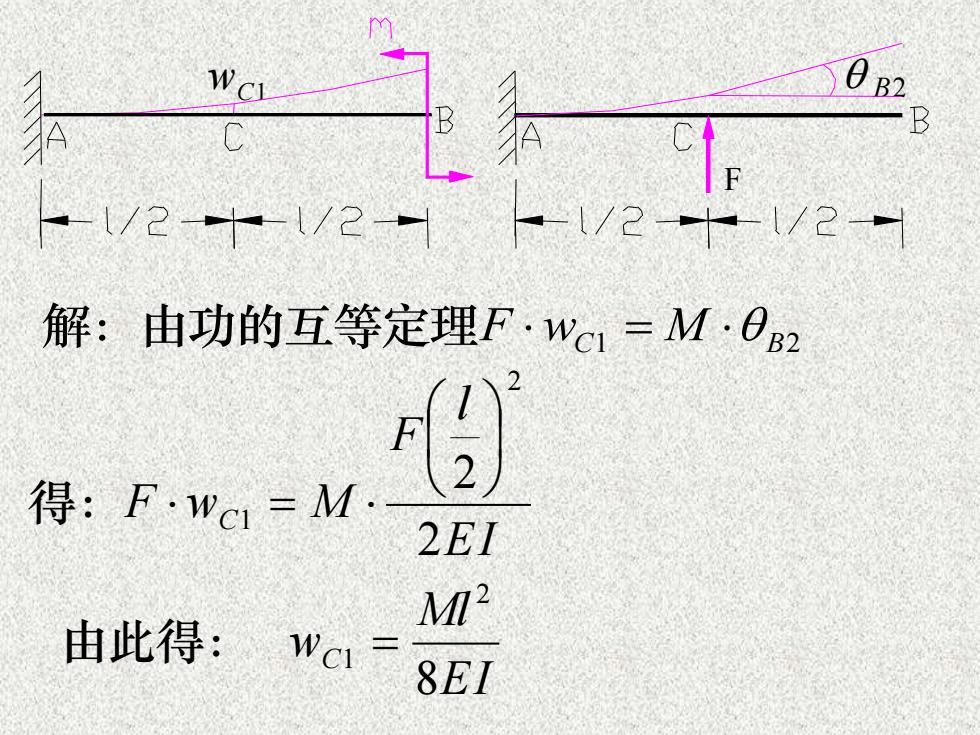
0 B2WCB解:由功的互等定理F·wci=M·OB1RD(2)得: F·wcl = M2EIMI?由此得:Wc8EI
wC1 B2 F wC1 M B2 解:由功的互等定理 = EI l F F wC M 2 2 2 1 得: = EI Ml wC 8 2 由此得: 1 = F

13-5卡氏定理FFV,=W-+Foi++Fo ++F,o, +.dS,SF+ AFS若只给 F以增量,其余不变,在△F作用下,原各力作用点将产生位移AAS.....,AS....变形能的增加量:AAF,AS, + FAS, + F,AS, +... + F,AS, +
13-5 卡氏定理 = = 1 1 + 2 2 + 3 3 + 2 1 2 1 2 1 V W F F F F1 F2 F3 1 2 3 i 若只给 以增量 ,其余不变,在 作用下,原各力作用点将产 生位移 Fi Fi 1 , 2 , , i , 变形能的增加量: V = Fi i + F1 1 + F2 2 ++ Fi i + 2 1 + Fi
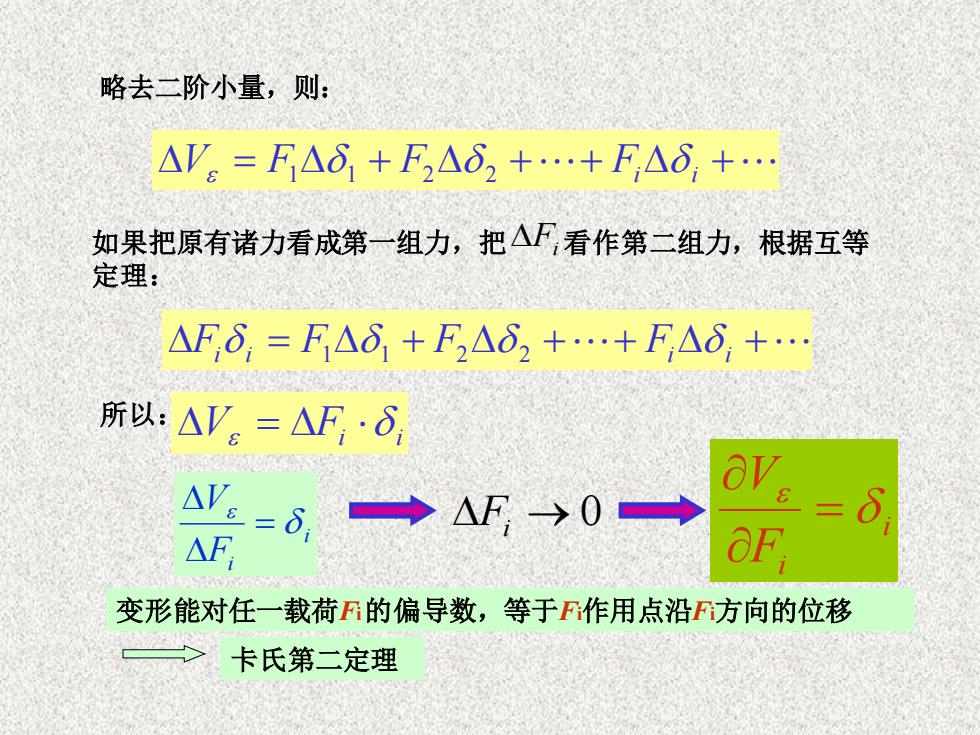
略去二阶小量,则:AV = FAS + FAS, +...+FAS +..如果把原有诸力看成第一组力,把△F 看作第二组力,根据互等定理:AFS, =FAS, + F,AS, +...+FAS, +..所以:△V, = △F, ·8avAV.SNF →0=8aFAF变形能对任一载荷F的偏导数,等于F作用点沿F方向的位移卡氏第二定理
略去二阶小量,则: V = F1 1 + F2 2 ++ Fi i + 如果把原有诸力看成第一组力,把 看作第二组力,根据互等 定理: Fi Fi i = F1 1 + F2 2 ++ Fi i + 所以: V Fi i = i Fi V = Fi → 0 i Fi V = 变形能对任一载荷Fi 的偏导数,等于Fi作用点沿Fi方向的位移 卡氏第二定理

推导过程使用了互等定理,所以只适用线弹性结构。横力弯曲:avaM?(x)WdxSi一aFaF2EIaM(x)M(x)dxEIaF桁架杆件受拉压:OFNFLFn,L,aVsV.-2SaFaFEA,2EAi=-1轴受扭矩作用:avaT(x)T(x)dxSaFGIaF
推导过程使用了互等定理,所以只适用线弹性结构。 横力弯曲: = = = L i i i L i dx F M x EI M x dx EI M x F F V ( ) ( ) ) 2 ( ) ( 2 桁架杆件受拉压: = = n j j N j j EA F L V 1 2 2 = = = n j i N j j N j j i i F F EA F L F V 1 轴受扭矩作用: = = i L P i i dx F T x G I T x F V ( ) ( )