内蒙古科技大学：《材料力学》课程PPT教学课件（土木类）总复习

材料力学总复习

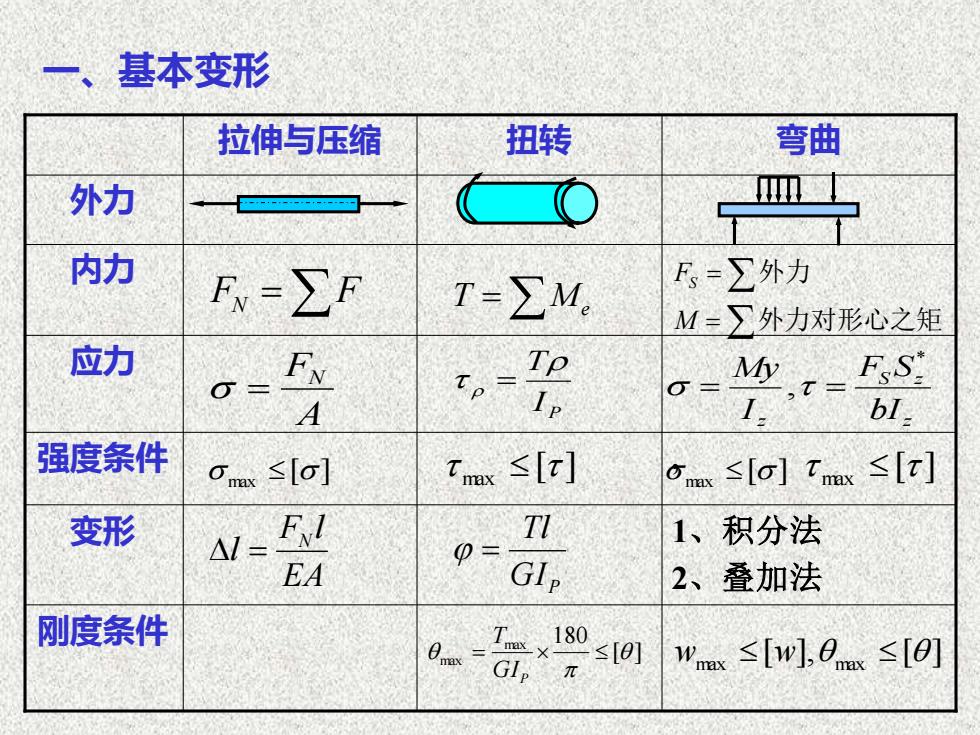
基本变形扭转弯曲拉伸与压缩外力内力F-Z外力FN-ZFT-Em.M-外力对形心之矩应力TpF,S.FNMyIpbl.A1强度条件≤[t]omex ≤[o] Tmax ≤[t]≤[α]maxTIFNI变形1、积分法NI=@GI,EA2、叠加法刚度条件180mex≤[0]≤[w],0mex ≤[0]0mWmexGI,T

一、基本变形 刚度条件 内力 1、积分法 2、叠加法 变形 强度条件 , 应力 外力 拉伸与压缩 扭转 弯曲 FN =F T =Me   = = 外力对形心之矩 外力 M FS A FN  = P I T   = z S z z bI F S I My *  = , = [ ]  max   [ ] max    [ ]  max   [ ] max    EA F l l N  = GIP Tl  = [ ] max 180 max    =   GIP T [ ], [ ] wmax  w  max  

应力状态分析.强度理论1、一点处的应力状态2、平面应力状态分析（1）斜截面上的应力or+o00A-cos2α - t, sin 2α-2oO sin 2α +t, cos 2α2（2）主平面和主应力O.arctanao2

二、应力状态分析.强度理论 1、一点处的应力状态 2、平面应力状态分析 （1）斜截面上的应力          cos 2 sin 2 2 2 x x y x y − − + + =        sin 2 cos 2 2 x x y + − = （2）主平面和主应力 2 2 2 1 2 2 x x y x y        +         −  + =         − − = x y x     2 arctan 2 1 0

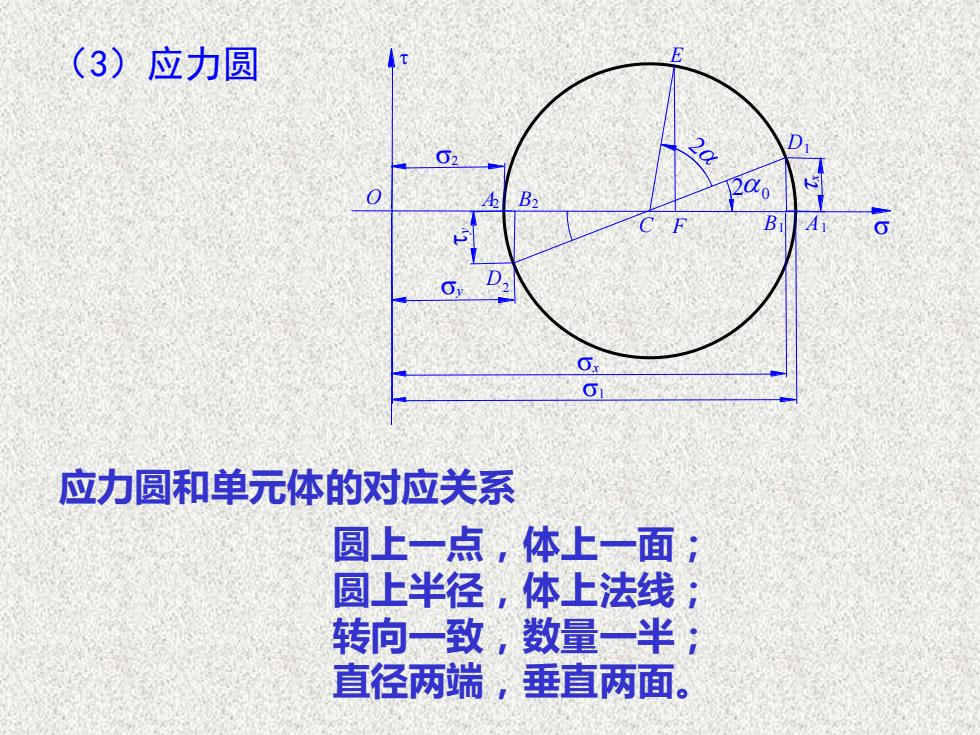
E（3）应力圆O0BAOOxa应力圆和单元体的对应关系圆上一点，体上一面；圆上半径，体上法线菜转向一致，数量一半直径两端，垂直两面

（3）应力圆  O  C 2 F B1 A1 A2 B2 D1 D2 E x y y x 1 2 0 应力圆和单元体的对应关系 圆上一点，体上一面； 圆上半径，体上法线； 转向一致，数量一半； 直径两端，垂直两面

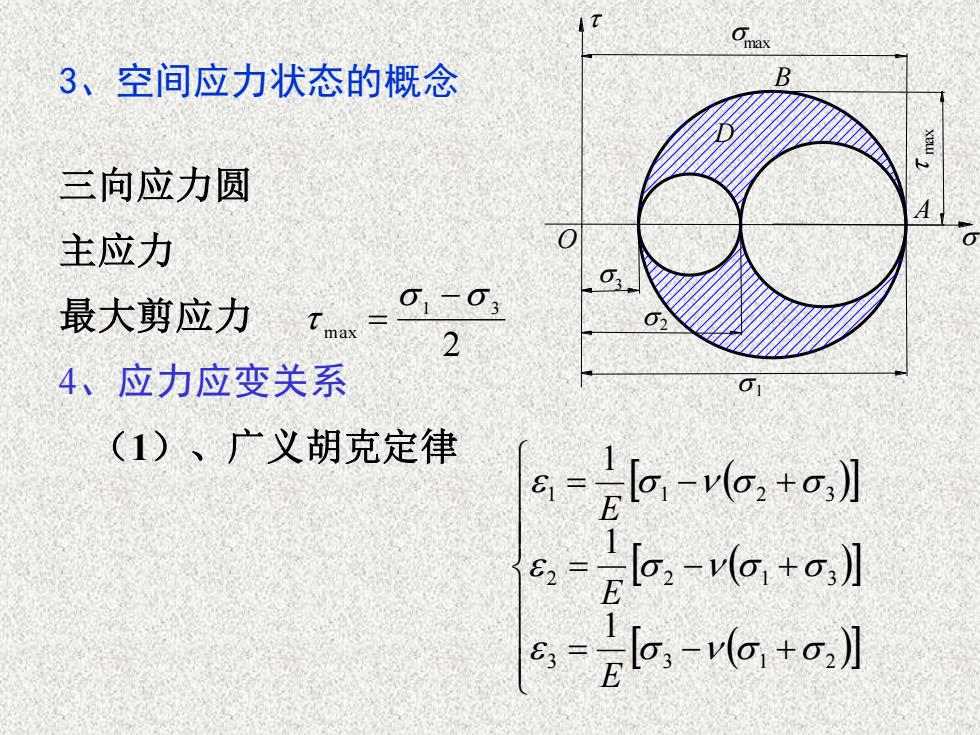
1OmaB3、空间应力状态的概念三向应力圆A0C主应力O.a.-g.最大剪应力Tmax24、应力应变关系ai（1）、广义胡克定律[G-- -[0, -v(o, +0,)]E一62[0, -v(0, +0, ]一63S

3、空间应力状态的概念 最大剪应力 2 1 3 max    − = 4、应力应变关系  ( )  ( )  ( )  = − + = − + = − + 3 3 1 2 2 2 1 3 1 1 2 3 111                EEE 主应力 三向应力圆   O 3 2 1 max B D A max （ 1）、广义胡克定律