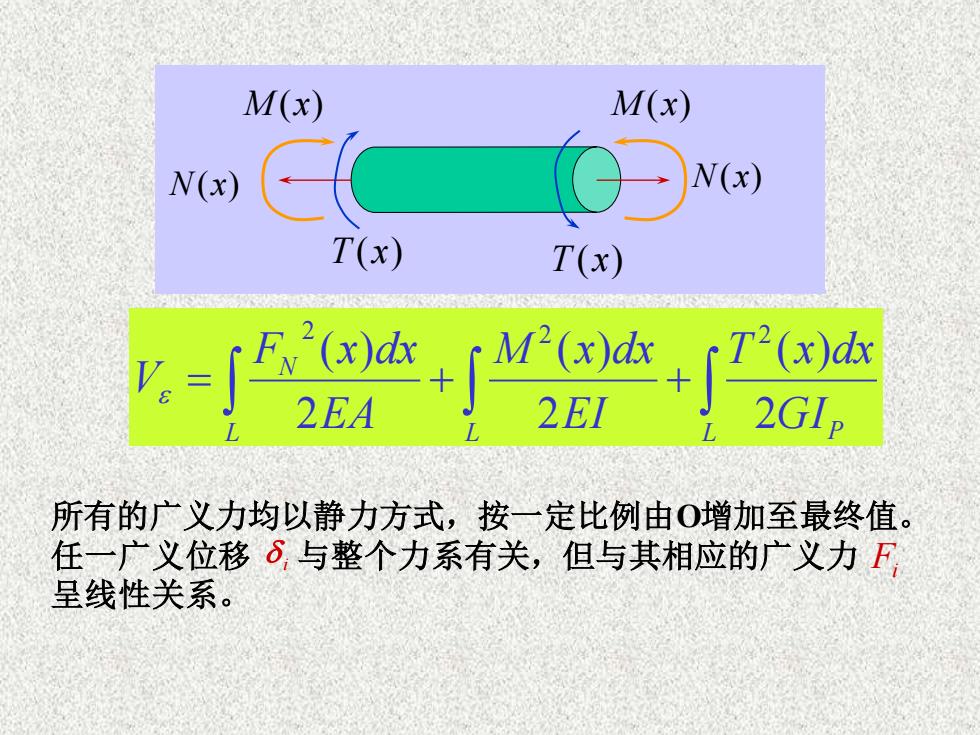
M(x)M(x)N(x)N(x)T(x)T(x)M(x)dxT2(x)dxFN(x)dx三2EA2EI2GIp所有的广义力均以静力方式,按一定比例由O增加至最终值。任一广义位移 S 与整个力系有关,但与其相应的广义力 F呈线性关系
N(x) N(x) M (x) M (x) T (x) T (x) = + + L L L P N G I T x dx EI M x dx EA F x dx V 2 ( ) 2 ( ) 2 ( ) 2 2 2 所有的广义力均以静力方式,按一定比例由O增加至最终值。 任一广义位移 与整个力系有关,但与其相应的广义力 呈线性关系。 i Fi

例:试求图示悬臂梁的应变能,并利用功能原理求自由端B的挠度。解:M(x)--F.xF2/3M(x)dxL2EI6EIF/3I F-Wβ由V, =W, 得WB -W-23EI
例:试求图示悬臂梁的应变能,并利用功 能原理求自由端B的挠度。 F x l 解: M (x) = −F x = = l EI F l x EI M x V 6 d 2 ( ) 2 2 3 W F wB = 2 1 由V = W,得 EI Fl wB 3 3 =
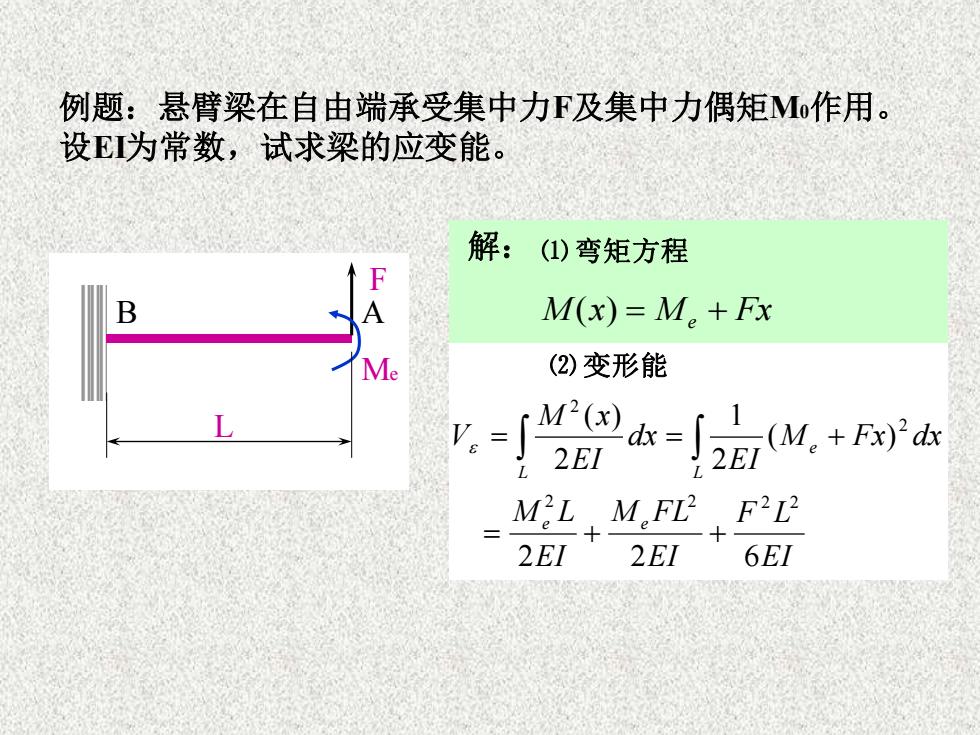
例题:悬臂梁在自由端承受集中力F及集中力偶矩Mo作用。设EI为常数,试求梁的应变能。解:(1)弯矩方程FAM(x) = M。+ FxB(2) 变形能MeM?(x)小M。+ Fx)"dx2EI2EILLF?L?M?LM,FL?2EI2EI6EI
例题:悬臂梁在自由端承受集中力F及集中力偶矩M0作用。 设EI为常数,试求梁的应变能。 L F Me B A 解: ⑴ 弯矩方程 M x M Fx ( ) = e + ⑵ 变形能 EI F L EI M FL EI M L M Fx dx EI dx EI M x V e e L e L 2 2 6 ( ) 2 1 2 ( ) 2 2 2 2 2 2 = + + = = +
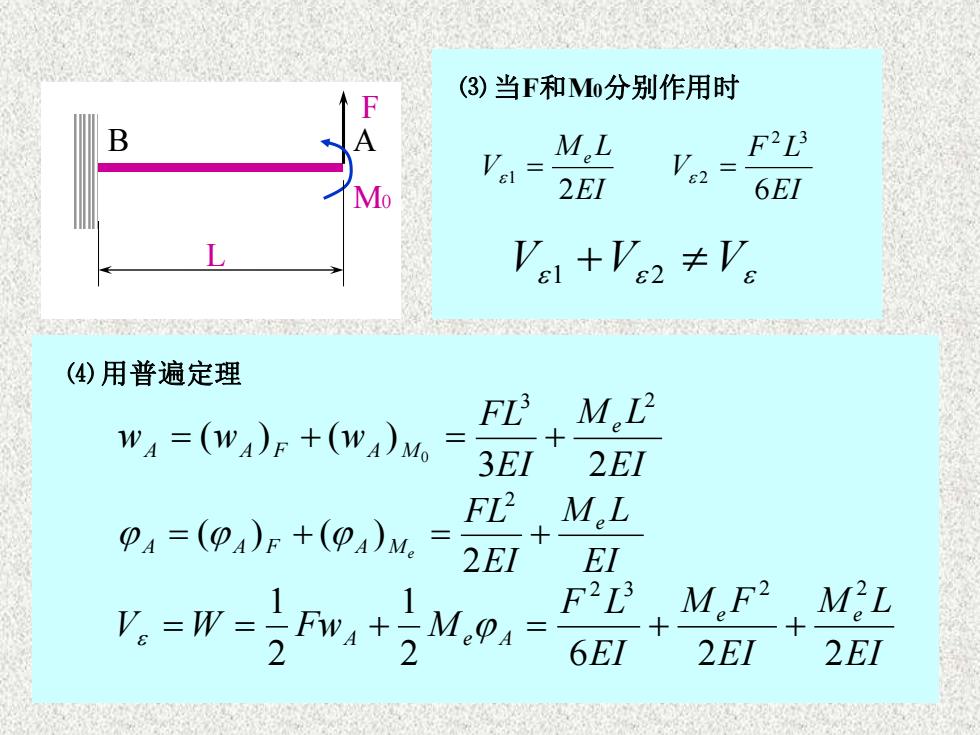
(3)当F和Mo分别作用时FABF?L3M.LVe2EI6EIMoV+Ve1 +V.628(4)用普遍定理M.L?FL3+WA =(wA), +(WA)Mo3EI2EIFL?M.LPA =(PA) +(PA)M。2EIEIM.F2M?LF2L3=M.PAV.=W=FWA一++22EI26EI2EI
L F M0 B A ⑶ 当F和M0分别作用时 EI F L V EI M L V e 2 6 2 3 1 = 2 = V1 +V 2 V ⑷ 用普遍定理 EI M L EI FL w w w e A A F A M 3 2 ( ) ( ) 3 2 0 = + = + EI M L EI FL e A A F A Me = + = + 2 ( ) ( ) 2 EI M L EI M F EI F L V W Fw M e e A e A 2 6 2 2 1 2 1 2 3 2 2 = = + = + +
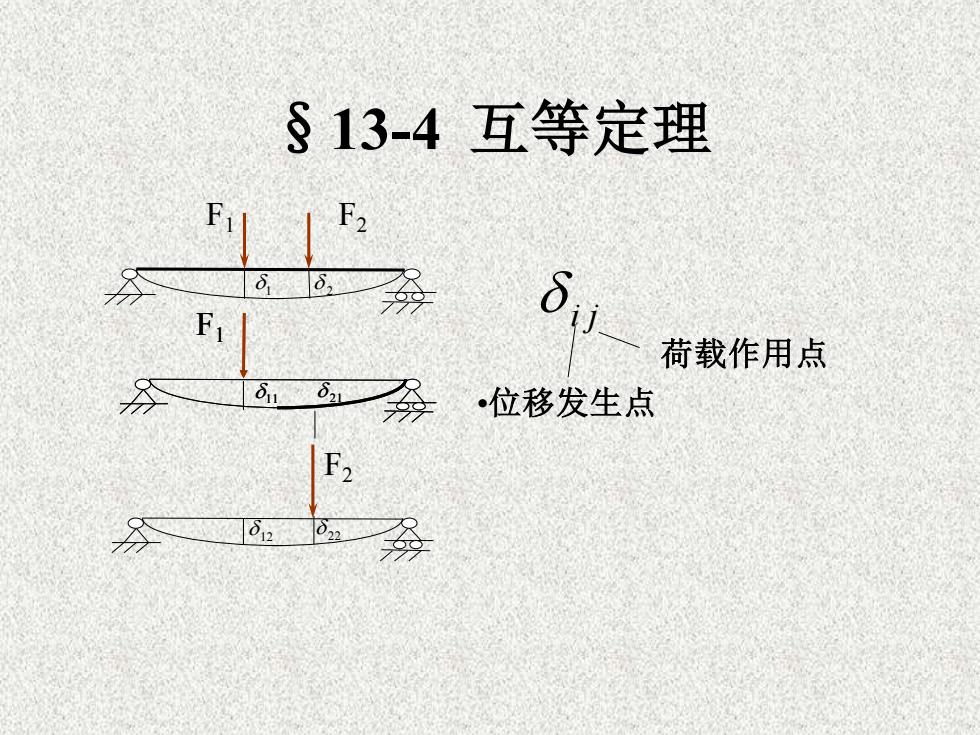
S 13-4 互等定理F2Fil6条SX11Fr荷载作用点A01 3 0茶·位移发生点F20 1012 902AA
§13-4 互等定理 i j •位移发生点 荷载作用点 1 2 F1 F2 F1 11 21 F2 12 22 11 21