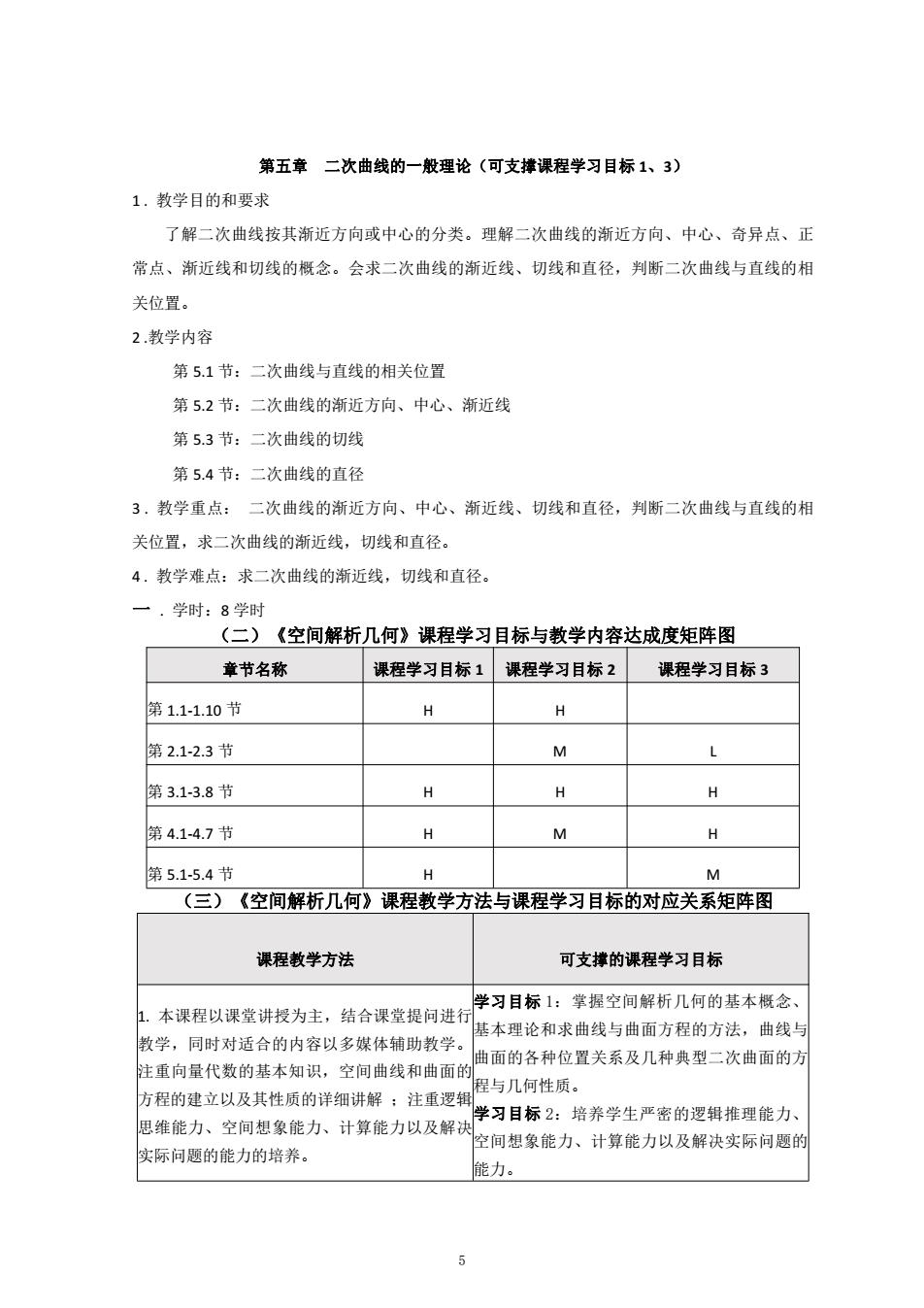
第五章二次曲线的一般理论(可支撑课程学习目标1、3) 1.教学目的和要求 了解二次曲线按其渐近方向或中心的分类。理解二次曲线的渐近方向、中心、奇异点、正 常点、渐近线和切线的概念。会求二次曲线的渐近线、切线和直径,判断二次曲线与直线的相 关位置。 2.教学内容 第5.1节:二次曲线与直线的相关位置 第5.2节:二次曲线的渐近方向、中心、渐近线 第5.3节:二次曲线的切线 第5.4节:二次曲线的直径 3.教学重点:二次曲线的渐近方向、中心、渐近线、切线和直径,判断二次曲线与直线的相 关位置,求二次曲线的渐近线,切线和直径。 4.教学难点:求二次曲线的渐近线,切线和直径。 一.学时:8学时 (二)《空间解析几何》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标1 课程学习目标2 课程学习目标3 第1.1-1.10节 H H 第2.1-2.3节 M 第3.1-3.8节 H H 夕 第4.1-4.7节 H M H 第5.1-5.4节 H M (三)《空间解析几何》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 学习目标1:掌握空间解析几何的基本概念、 1.本课程以课堂讲授为主,结合课堂提问进行 基本理论和求曲线与曲面方程的方法,曲线与 教学,同时对适合的内容以多媒体辅助教学。 曲面的各种位置关系及几种典型二次曲面的方 注重向量代数的基本知识,空间曲线和曲面的 程与几何性质。 方程的建立以及其性质的详细讲解:注重逻辑 学习目标2:培养学生严密的逻辑推理能力、 思维能力、空间想象能力、计算能力以及解决 空间想象能力、计算能力以及解决实际问题的 实际问题的能力的培养。 能力。 5
第五章 二次曲线的一般理论(可支撑课程学习目标 1、3) 1 . 教学目的和要求 了解二次曲线按其渐近方向或中心的分类。理解二次曲线的渐近方向、中心、奇异点、正 常点、渐近线和切线的概念。会求二次曲线的渐近线、切线和直径,判断二次曲线与直线的相 关位置。 2 .教学内容 第 5.1 节:二次曲线与直线的相关位置 第 5.2 节:二次曲线的渐近方向、中心、渐近线 第 5.3 节:二次曲线的切线 第 5.4 节:二次曲线的直径 3 . 教学重点: 二次曲线的渐近方向、中心、渐近线、切线和直径,判断二次曲线与直线的相 关位置,求二次曲线的渐近线,切线和直径。 4 . 教学难点:求二次曲线的渐近线,切线和直径。 一 . 学时:8 学时 (二)《空间解析几何》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标 1 课程学习目标 2 课程学习目标 3 第 1.1-1.10 节 H H 第 2.1-2.3 节 M L 第 3.1-3.8 节 H H H 第 4.1-4.7 节 H M H 第 5.1-5.4 节 H M (三)《空间解析几何》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 1. 本课程以课堂讲授为主,结合课堂提问进行 教学,同时对适合的内容以多媒体辅助教学。 注重向量代数的基本知识,空间曲线和曲面的 方程的建立以及其性质的详细讲解 ;注重逻辑 思维能力、空间想象能力、计算能力以及解决 实际问题的能力的培养。 学习目标 1:掌握空间解析几何的基本概念、 基本理论和求曲线与曲面方程的方法,曲线与 曲面的各种位置关系及几种典型二次曲面的方 程与几何性质。 学习目标 2:培养学生严密的逻辑推理能力、 空间想象能力、计算能力以及解决实际问题的 能力。 5
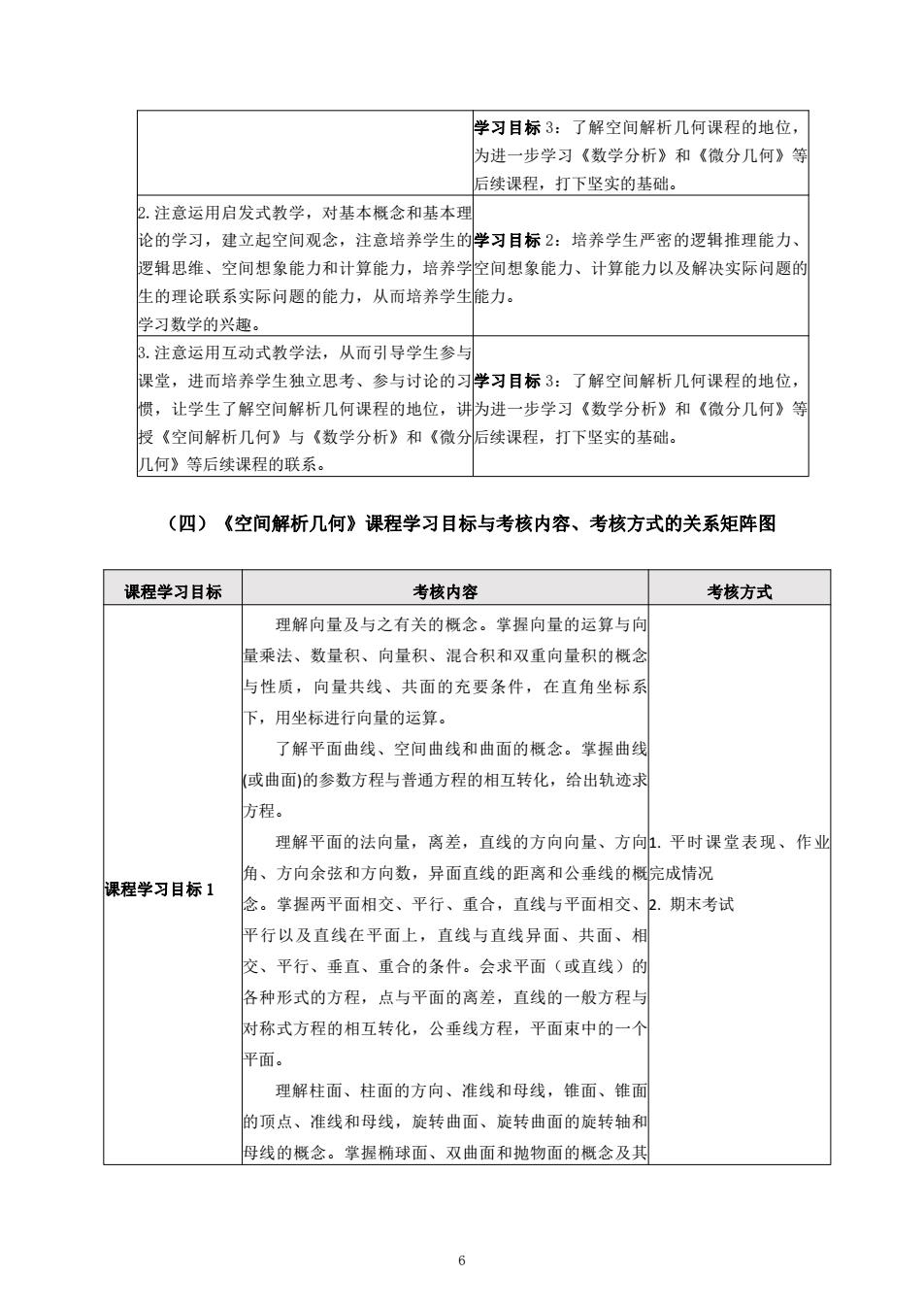
学习目标3:了解空间解析几何课程的地位, 为进一步学习《数学分析》和《微分几何》等 后续课程,打下坚实的基础。 2.注意运用启发式教学,对基本概念和基本理 论的学习,建立起空间观念,注意培养学生的学习目标2:培养学生严密的逻辑推理能力、 逻辑思维、空间想象能力和计算能力,培养学空间想象能力、计算能力以及解决实际问题的 生的理论联系实际问题的能力,从而培养学生能力。 学习数学的兴趣。 3.注意运用互动式教学法,从而引导学生参与 课堂,进而培养学生独立思考、参与讨论的习学习目标3:了解空间解析几何课程的地位, 惯,让学生了解空间解析几何课程的地位,讲伪进一步学习《数学分析》和《微分几何》等 授《空间解析几何》与《数学分析》和《微分后续课程,打下坚实的基础。 几何》等后续课程的联系。 (四)《空间解析几何》课程学习目标与考核内容、考核方式的关系矩阵图 课程学习目标 考核内容 考核方式 理解向量及与之有关的概念。掌握向量的运算与向 量乘法、数量积、向量积、混合积和双重向量积的概念 与性质,向量共线、共面的充要条件,在直角坐标系 下,用坐标进行向量的运算。 了解平面曲线、空间曲线和曲面的概念。掌握曲线 或曲面)的参数方程与普通方程的相互转化,给出轨迹求 方程。 理解平面的法向量,离差,直线的方向向量、方向.平时课堂表现、作业 角、方向余弦和方向数,异面直线的距离和公垂线的概完成情况 课程学习目标1 念。掌握两平面相交、平行、重合,直线与平面相交、2.期末考试 平行以及直线在平面上,直线与直线异面、共面、相 交、平行、垂直、重合的条件。会求平面(或直线)的 各种形式的方程,点与平面的离差,直线的一般方程与 对称式方程的相互转化,公垂线方程,平面束中的一个 平面。 理解柱面、柱面的方向、准线和母线,锥面、锥面 的顶点、准线和母线,旋转曲面、旋转曲面的旋转轴和 母线的概念。掌握椭球面、双曲面和抛物面的概念及其 6
学习目标 3:了解空间解析几何课程的地位, 为进一步学习《数学分析》和《微分几何》等 后续课程,打下坚实的基础。 2.注意运用启发式教学,对基本概念和基本理 论的学习,建立起空间观念,注意培养学生的 逻辑思维、空间想象能力和计算能力,培养学 生的理论联系实际问题的能力,从而培养学生 学习数学的兴趣。 学习目标 2:培养学生严密的逻辑推理能力、 空间想象能力、计算能力以及解决实际问题的 能力。 3.注意运用互动式教学法,从而引导学生参与 课堂,进而培养学生独立思考、参与讨论的习 惯,让学生了解空间解析几何课程的地位,讲 授《空间解析几何》与《数学分析》和《微分 几何》等后续课程的联系。 学习目标 3:了解空间解析几何课程的地位, 为进一步学习《数学分析》和《微分几何》等 后续课程,打下坚实的基础。 (四)《空间解析几何》课程学习目标与考核内容、考核方式的关系矩阵图 课程学习目标 考核内容 考核方式 课程学习目标 1 理解向量及与之有关的概念。掌握向量的运算与向 量乘法、数量积、向量积、混合积和双重向量积的概念 与性质,向量共线、共面的充要条件,在直角坐标系 下,用坐标进行向量的运算。 了解平面曲线、空间曲线和曲面的概念。掌握曲线 (或曲面)的参数方程与普通方程的相互转化,给出轨迹求 方程。 理解平面的法向量,离差,直线的方向向量、方向 角、方向余弦和方向数,异面直线的距离和公垂线的概 念。掌握两平面相交、平行、重合,直线与平面相交、 平行以及直线在平面上,直线与直线异面、共面、相 交、平行、垂直、重合的条件。会求平面(或直线)的 各种形式的方程,点与平面的离差,直线的一般方程与 对称式方程的相互转化,公垂线方程,平面束中的一个 平面。 理解柱面、柱面的方向、准线和母线,锥面、锥面 的顶点、准线和母线,旋转曲面、旋转曲面的旋转轴和 母线的概念。掌握椭球面、双曲面和抛物面的概念及其 1. 平时课堂表现、作业 完成情况 2. 期末考试 6
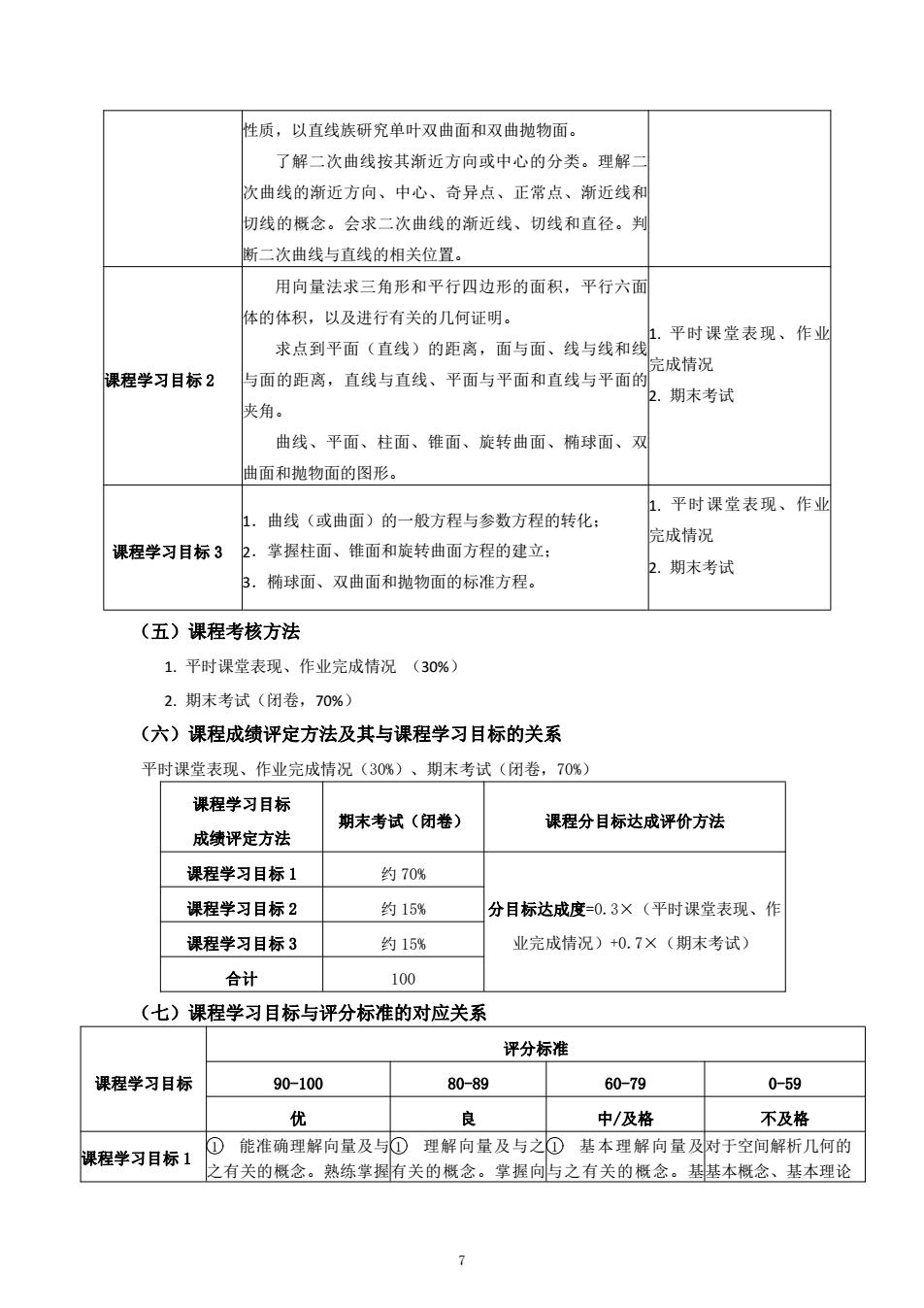
性质,以直线族研究单叶双曲面和双曲抛物面。 了解二次曲线按其渐近方向或中心的分类。理解 次曲线的渐近方向、中心、奇异点、正常点、渐近线和 切线的概念。会求二次曲线的渐近线、切线和直径。判 断二次曲线与直线的相关位置。 用向量法求三角形和平行四边形的面积,平行六面 体的体积,以及进行有关的几何证明。 . 平时课堂表现、作业 求点到平面(直线)的距离,面与面、线与线和线 完成情况 课程学习目标2 与面的距离,直线与直线、平面与平面和直线与平面的 . 期末考试 夹角。 曲线、平面、柱面、锥面、旋转曲面、椭球面、双 曲面和抛物面的图形。 1. 平时课堂表现、作业 1. 曲线(或曲面)的一般方程与参数方程的转化: 完成情况 课程学习目标3 2. 掌握柱面、锥面和旋转曲面方程的建立: 2.期末考试 椭球面、双曲面和抛物面的标准方程。 (五)课程考核方法 1.平时课堂表现、作业完成情况(30%) 2.期末考试(闭卷,70%) (六)课程成绩评定方法及其与课程学习目标的关系 平时课堂表现、作业完成情况(30%)、期末考试(闭卷,70%) 课程学习目标 期末考试(闭卷) 课程分目标达成评价方法 成绩评定方法 课程学习目标1 约70% 课程学习目标2 约15% 分目标达成度=0.3×(平时课堂表现、作 课程学习目标3 约15% 业完成情况)+0.7×(期末考试) 合计 100 (七)课程学习目标与评分标准的对应关系 评分标准 课程学习目标 90-100 80-89 60-79 0-59 优 良 中/及格 不及格 ①能准确理解向量及与①理解向量及与之①基本理解向量及对于空间解析几何的 课程学习目标1 之有关的概念。熟练掌握有关的概念。掌握向与之有关的概念。基基本概念、基本理论
性质,以直线族研究单叶双曲面和双曲抛物面。 了解二次曲线按其渐近方向或中心的分类。理解二 次曲线的渐近方向、中心、奇异点、正常点、渐近线和 切线的概念。会求二次曲线的渐近线、切线和直径。判 断二次曲线与直线的相关位置。 课程学习目标 2 用向量法求三角形和平行四边形的面积,平行六面 体的体积,以及进行有关的几何证明。 求点到平面(直线)的距离,面与面、线与线和线 与面的距离,直线与直线、平面与平面和直线与平面的 夹角。 曲线、平面、柱面、锥面、旋转曲面、椭球面、双 曲面和抛物面的图形。 1. 平时课堂表现、作业 完成情况 2. 期末考试 课程学习目标 3 1.曲线(或曲面)的一般方程与参数方程的转化; 2.掌握柱面、锥面和旋转曲面方程的建立; 3.椭球面、双曲面和抛物面的标准方程。 1. 平时课堂表现、作业 完成情况 2. 期末考试 (五)课程考核方法 1. 平时课堂表现、作业完成情况 (30%) 2. 期末考试(闭卷,70%) (六)课程成绩评定方法及其与课程学习目标的关系 平时课堂表现、作业完成情况(30%)、期末考试(闭卷,70%) 课程学习目标 成绩评定方法 期末考试(闭卷) 课程分目标达成评价方法 课程学习目标 1 约 70% 分目标达成度=0.3×(平时课堂表现、作 业完成情况)+0.7×(期末考试) 课程学习目标 2 约 15% 课程学习目标 3 约 15% 合计 100 (七)课程学习目标与评分标准的对应关系 课程学习目标 评分标准 90-100 80-89 60-79 0-59 优 良 中/及格 不及格 课程学习目标 1 1 能准确理解向量及与 之有关的概念。熟练掌握 1 理解向量及与之 有关的概念。掌握向 1 基本理解向量及 与之有关的概念。基 对于空间解析几何的 基本概念、基本理论 7

向量的运算与向量乘法、量的运算与向量乘本掌握向量的运算与和求轨迹方程的方法 数量积、向量积、混合积法、数量积、向量向量乘法、数量积、 掌握比较欠缺。 和双重向量积的概念与性积、混合积和双重向向量积、混合积和双 质,向量共线、共面的充量积的概念与性质,重向量积的概念与性 要条件,在直角坐标系向量共线、共面的充质,向量共线、共面 下,用坐标进行向量的运腰条件,在直角坐标的充要条件,在直角 算。 系下,用坐标进行向坐标系下,用坐标进 ② 了解平面曲线、空间量的运算。 行向量的运算 曲线和曲面的概念。熟练②了解平面曲线、②了解平面曲线、 掌握曲线(或曲面)的参数空间曲线和曲面的概空间曲线和曲面的概 方程与普通方程的相互转念。掌握曲线(或曲念。基本掌握曲线(或 化,给出轨迹求方程。 面)的参数方程与普通曲面)的参数方程与普 ③能准确理解平面的法方程的相互转化,给通方程的相互转化, 向量,离差,直线的方向出轨迹求方程。 给出轨迹求方程。 向量、方向角、方向余弦③能理解平面的法能基本理解平面的法 和方向数,异面直线的距向量,离差,直线的向量,离差,直线的 离和公垂线的概念。熟练方向向量、方向角、方向向量、方向角、 掌握两平面相交、平行、方向余弦和方向数, 方向余弦和方向数, 重合的条件,直线与平面异面直线的距离和公异面直线的距离和公 相交、平行以及直线在平垂线的概念。掌握两垂线的概念。基本掌 面上的条件,直线与直线平面相交、平行、重 握两平面相交、平 异面、共面、相交、平合的条件,直线与平行、重合的条件,直 行、垂直、重合的条件。面相交、平行以及直线与平面相交、平行 能熟练求出平面(或直线在平面上的条件,以及直线在平面上的 线)的各种形式的方程,直线与直线异面、共条件,直线与直线异 点与平面的离差,直线的面、相交、平行、垂面、共面、相交、平 般方程与对称式方程的直、重合的条件。能行、垂直、重合的条 相互转化,公垂线方程,求出平面(或直线) 件。能基本求出平面 平面束中的一个平面。 的各种形式的方程, (或直线)的各种形 4 能准确理解柱面、柱点与平面的离差,直式的方程,点与平面 面的方向、准线和母线,线的一般方程与对称的离差,直线的一般 锥面、锥面的顶点、准线式方程的相互转化, 方程与对称式方程的 和母线,旋转曲面、旋转公垂线方程,平面束相互转化,公垂线方 曲面的旋转轴和母线的概中的一个平面。 程,平面束中的一个 念。熟练掌握椭球面、双④能理解柱面、柱 平面。 曲面和抛物面的概念及其面的方向、准线和母③能基本理解柱 性质,以直线族研究单叶线,锥面、锥面的顶面、柱面的方向、准 双曲面和双曲抛物面。 点、准线和母线,旋线和母线,锥面、锥 ⑤了解二次曲线按其渐转曲面、旋转曲面的面的顶点、准线和母 近方向或中心的分类。能旋转轴和母线的概线,旋转曲面、旋转 准确理解二次曲线的渐近念。掌握椭球面、双曲面的旋转轴和母线 方向、中心、奇异点、正曲面和抛物面的概念的概念。基本掌握椭 常点、渐近线和切线的概及其性质,以直线族球面、双曲面和抛物
向量的运算与向量乘法、 数量积、向量积、混合积 和双重向量积的概念与性 质,向量共线、共面的充 要条件,在直角坐标系 下,用坐标进行向量的运 算。 2 了解平面曲线、空间 曲线和曲面的概念。熟练 掌握曲线(或曲面)的参数 方程与普通方程的相互转 化,给出轨迹求方程。 3 能准确理解平面的法 向量,离差,直线的方向 向量、方向角、方向余弦 和方向数,异面直线的距 离和公垂线的概念。熟练 掌握两平面相交、平行、 重合的条件,直线与平面 相交、平行以及直线在平 面上的条件,直线与直线 异面、共面、相交、平 行、垂直、重合的条件。 能熟练求出平面(或直 线)的各种形式的方程, 点与平面的离差,直线的 一般方程与对称式方程的 相互转化,公垂线方程, 平面束中的一个平面。 4 能准确理解柱面、柱 面的方向、准线和母线, 锥面、锥面的顶点、准线 和母线,旋转曲面、旋转 曲面的旋转轴和母线的概 念。熟练掌握椭球面、双 曲面和抛物面的概念及其 性质,以直线族研究单叶 双曲面和双曲抛物面。 5 了解二次曲线按其渐 近方向或中心的分类。能 准确理解二次曲线的渐近 方向、中心、奇异点、正 常点、渐近线和切线的概 量 的 运 算 与 向 量 乘 法 、 数 量 积 、 向 量 积、混合积和双重向 量积的概念与性质, 向量共线、共面的充 要条件,在直角坐标 系下,用坐标进行向 量的运算。 2 了解平面曲线、 空间曲线和曲面的概 念。掌握曲线(或曲 面)的参数方程与普通 方程的相互转化,给 出轨迹求方程。 3 能理解平面的法 向量,离差,直线的 方向向量、方向角、 方向余弦和方向数, 异面直线的距离和公 垂线的概念。掌握两 平面相交、平行、重 合的条件,直线与平 面相交、平行以及直 线在平面上的条件, 直线与直线异面、共 面、相交、平行、垂 直、重合的条件。能 求出平面(或直线) 的各种形式的方程, 点与平面的离差,直 线的一般方程与对称 式方程的相互转化, 公垂线方程,平面束 中的一个平面。 4 能理解柱面、柱 面的方向、准线和母 线,锥面、锥面的顶 点、准线和母线,旋 转曲面、旋转曲面的 旋 转 轴 和 母 线 的 概 念。掌握椭球面、双 曲面和抛物面的概念 及其性质,以直线族 本掌握向量的运算与 向量乘法、数量积、 向量积、混合积和双 重向量积的概念与性 质,向量共线、共面 的充要条件,在直角 坐标系下,用坐标进 行向量的运算 2 了解平面曲线、 空间曲线和曲面的概 念。基本掌握曲线(或 曲面)的参数方程与普 通方程的相互转化, 给出轨迹求方程。 能基本理解平面的法 向量,离差,直线的 方向向量、方向角、 方向余弦和方向数, 异面直线的距离和公 垂线的概念。基本掌 握两平面相交、平 行、重合的条件,直 线与平面相交、平行 以及直线在平面上的 条件,直线与直线异 面、共面、相交、平 行、垂直、重合的条 件。能基本求出平面 (或直线)的各种形 式的方程,点与平面 的离差,直线的一般 方程与对称式方程的 相互转化,公垂线方 程,平面束中的一个 平面。 3 能 基 本 理 解 柱 面、柱面的方向、准 线和母线,锥面、锥 面的顶点、准线和母 线,旋转曲面、旋转 曲面的旋转轴和母线 的概念。基本掌握椭 球面、双曲面和抛物 和求轨迹方程的方法 掌握比较欠缺。 8

念。能熟练求出二次曲线研究单叶双曲面和双面的概念及其性质, 的渐近线、切线和直径。 曲抛物面。 以直线族研究单叶双 能准确判断二次曲线与直⑤能理解二次曲线曲面和双曲抛物面。 线的相关位置。 的渐近方向、中心、④能基本理解二次 奇异点、正常点、渐曲线的渐近方向、中 近线和切线的概念。心、奇异点、正常 能求出二次曲线的渐点、渐近线和切线的 近线、切线和直径。概念。能基本求出 会判断二次曲线与直次曲线的渐近线、切 线的相关位置。 线和直径。会判断 些二次曲线与直线的 相关位置。 ① 能熟练用向量法求三①能用向量法求三 ①基本会用向量法 对于用向量法求三角 角形和平行四边形的面角形和平行四边形的 求三角形和平行四边 形和平行四边形的面 积,平行六面体的体积,面积,平行六面体的 形的面积,平行六面 积,平行六面体的体 以及进行有关的几何证体积,以及进行有关体的体积,以及进行 积,以及进行有关的 明: 的几何证明: 些简单的几何证 几何证明:求点到平 ②能熟练求出点到平面②能求出点到平面明: 面(或直线)的距 (或直线)的距离,面与(或直线)的距离,②能基本求出点到 离,面与面、线与线 面、线与线和线与面的距面与面、线与线和线平面(或直线)的距 和线与面的距离,直 离,直线与直线、平面与与面的距离,直线与离,面与面、线与线 线与直线、平面与平 课程学习目标2 平面和直线与平面的夹直线、平面与平面和和线与面的距离,直 面和直线与平面的夹 角: 直线与平面的夹角: 线与直线、平面与平 角:曲线、平面、柱 能熟练画出曲线、平③能画出曲线、平面和直线与平面的夹 面、锥面、旋转曲 面、柱面、锥面、旋转曲面、柱面、锥面、旋角: 面、椭球面、双曲面 面、椭球面、双曲面和抛转曲面、椭球面、双③ 能基本画出曲 和抛物面的图形缺乏 物面的图形。 曲面和抛物面的图线、平面、柱面、锥 了解与掌握。 形。 面、旋转曲面、椭球 面、双曲面和抛物面 的图形。 ①熟练掌握曲线(或曲O掌握曲线(或曲( ①基本掌握曲线 对于曲线(或曲面) 面)的一般方程与参数方面)的一般方程与参 (或曲面)的一般方 的方程,柱面、锥面 程的转化: 数方程的转化: 程与参数方程的转 和旋转曲面方程的建 ②熟练掌握柱面、锥面② 掌握柱面、锥面化: 立,椭球面、双曲面 和旋转曲面方程的建立: 和旋转曲面方程的建 ②基本掌握柱面、 和抛物面的标准方程 课程学习目标3 ③熟练掌握椭球面、双立: 锥面和旋转曲面方程 缺乏了解和掌握。 曲面和抛物面的标准方③掌握椭球面、双【 的建立: 程。 曲面和抛物面的标准 ③基本掌握椭球 方程。 面、双曲面和抛物面 的标准方程。 9
念。能熟练求出二次曲线 的渐近线、切线和直径。 能准确判断二次曲线与直 线的相关位置。 研究单叶双曲面和双 曲抛物面。 5 能理解二次曲线 的渐近方向、中心、 奇异点、正常点、渐 近线和切线的概念。 能求出二次曲线的渐 近线、切线和直径。 会判断二次曲线与直 线的相关位置。 面的概念及其性质, 以直线族研究单叶双 曲面和双曲抛物面。 4 能基本理解二次 曲线的渐近方向、中 心 、 奇 异 点 、 正 常 点、渐近线和切线的 概念。能基本求出二 次曲线的渐近线、切 线和直径。会判断一 些二次曲线与直线的 相关位置。 课程学习目标 2 1 能熟练用向量法求三 角形和平行四边形的面 积,平行六面体的体积, 以及进行有关的几何证 明; 2 能熟练求出点到平面 (或直线)的距离,面与 面、线与线和线与面的距 离,直线与直线、平面与 平面和直线与平面的夹 角; 3 能熟练画出曲线、平 面、柱面、锥面、旋转曲 面、椭球面、双曲面和抛 物面的图形。 1 能用向量法求三 角形和平行四边形的 面积,平行六面体的 体积,以及进行有关 的几何证明; 2 能求出点到平面 (或直线)的距离, 面与面、线与线和线 与面的距离,直线与 直线、平面与平面和 直线与平面的夹角; 3 能画出曲线、平 面、柱面、锥面、旋 转曲面、椭球面、双 曲 面 和 抛 物 面 的 图 形。 1 基本会用向量法 求三角形和平行四边 形的面积,平行六面 体的体积,以及进行 一些简单的几何证 明; 2 能基本求出点到 平面(或直线)的距 离,面与面、线与线 和线与面的距离,直 线与直线、平面与平 面和直线与平面的夹 角; 3 能基本画出曲 线、平面、柱面、锥 面、旋转曲面、椭球 面、双曲面和抛物面 的图形。 对于用向量法求三角 形和平行四边形的面 积,平行六面体的体 积,以及进行有关的 几何证明;求点到平 面 ( 或 直 线 ) 的 距 离,面与面、线与线 和线与面的距离,直 线与直线、平面与平 面和直线与平面的夹 角;曲线、平面、柱 面 、 锥 面 、 旋 转 曲 面、椭球面、双曲面 和抛物面的图形缺乏 了解与掌握。 课程学习目标 3 1 熟练掌握曲线(或曲 面)的一般方程与参数方 程的转化; 2 熟练掌握柱面、锥面 和旋转曲面方程的建立; 3 熟练掌握椭球面、双 曲面和抛物面的标准方 程。 1 掌握曲线(或曲 面)的一般方程与参 数方程的转化; 2 掌握柱面、锥面 和旋转曲面方程的建 立; 3 掌握椭球面、双 曲面和抛物面的标准 方程。 1 基本掌握曲线 (或曲面)的一般方 程与参数方程的转 化; 2 基本掌握柱面、 锥面和旋转曲面方程 的建立; 3 基本掌握椭球 面、双曲面和抛物面 的标准方程。 对于曲线(或曲面) 的方程,柱面、锥面 和旋转曲面方程的建 立,椭球面、双曲面 和抛物面的标准方程 缺乏了解和掌握。 9