
在均勾导体中,电位分布满足拉普拉斯方程。在均勾导体中,电位分布获得拉普拉斯方程的物理原因,与第4和5章中电准静态情况下导致拉普拉斯方程的物理原因是十分不间的,认识到这一点是重要的。当稳定传导时,决定性的要求是电流密度的散度为零。不成对的电荷密度并不影响电流分布,而是由它确定。在均勾导体中,连续性对了的约束碰巧意味着没有不成对的电荷密度。在不均勾导体中,式(4)表明有不成对电荷的积聚。确实,当α是位置的函数时,式(2)成为(6)V·E+E.V0=0一经求得电位分布,就可用高斯定律来确定不成对电荷密度的分布。(7)Pu=EV.E+E.ve方程(6)可以用来解出divE,然后将该量代人式(7),得到P=-E-Va+E-Ve(8)即使的分布在确定E时不起作用,但通过高斯定律,它却影响了不成对电荷密度的分布。连续性条件在电导率突然变化处,从式(2)和(3)可得出连续性条件。从式(2)导出的条件(9)n.(o,E*-o,Eb) =0正如从高斯定律得到的式(1.3.17)一样。由式(3)包含的连续性条件已在5.3节中熟悉。n×(E*-E)=00.-0=0(10)图例说明绝缘表面处的边界条件绝缘的导线和普通的电肌器是导电媒质被基本上是绝缘的媒质界定的例子。应该用什么边界条件来确导电材料内部的电流分布在图7.2.2中,区域(a)与区城(b)相比是相对绝缘的,0,《αb。由式(9)得出区域(a)中的法向电场比区域(b)中的大得多,》。根据式(10),E的切线分量是相等的,一。假定在绝缘区域内E的法向和切线分最的大小有相同的数量级的情况下,这两个语句分别建立了E的法向和切线分量的相对大小,示于图 7. 2. 2。 我们)可以断定在相对导电的区域(b)内,E的法向分量与切线分量相比基本上为零。因此,要在相对导电区域内确定场,在绝缘表面处使用的边界条件是(11)nJ=0->n.y@=0+ 194

在绝缘边界处,在导体内,电位的法向导数为零,而边界的电位调节它自身使这成为事实。电流线转变方狗使得它们保持与绝缘边界相切,如图7.2.2所示。正如包含在式(8)中的高斯定律在事后用来求出不成对的体电荷密度一样,高斯连续性条件式(6.5.3),可用来计算不成对的面电荷密度。与电流连续性条件式(9),结合在一起,它成为 (-)(12)电如果只有两个电极连接图7.2.1中的导体,从而只有一个电压=和一个电流=端口的电压-电流关系有如下的形式(13)G式中G为电导。为了使G与场量相联系,把式(2)对面S所包断的体积V进行积分,并且用高斯定理将体积分转换为电流gE·da对面 S的积分。于是此积分定律应用于图 7. 2. 1中所示的包围连接到正端钮的电极的表面。在那里它横切导线,贡献是一i,以致对闭合面的积分变成oE.da=0(14)式中S,是电位为的完纯导电电极与欧姆导体的界面。将式(14)除以端电压就得出由式(13)定义的电导的表达式。oE-da(15)注意决定电位分布的方程式(4)的线性性质保证i正比于。从而式(15)与无关,并且确实是表征与激励无关的系统的一个参数。对电导的式(15)与对电容的(6.5.6)式的比较,启示一种模拟,这将在7.6节中计论。导体中场的定性图素图7.2.3中说明三类稳定传导形式的特征。在第一类中,所关心的区域是一个有均勾电导率,被具有受约束电位的表面或被完纯绝缘体所界定。在第二类中,在界面处电导率有突变,但11.1148884F图7.2.3包含导电材料和完维导电电极的典型形式。(a)所关心的区城充满具有均匀电导率的材料。(b)由不同的有均勾电导率的材料构成的区域。在界面处电导率不连续。(c)电导率卡滑地变化。195

数量是有限的,而在第三类中,电导率是平滑地变化的。因为高斯定律在确定电位分布时不起作用,在这三类形式中介电常数的分布是任意的。当然,它们对于所引起的不成对电荷密度的分布有强烈影响。在导体内电场分布的定性图景是根据类似于6.5节对线性电介质所用的论证形成的。因为J是无做的,并与E有相同的方向,它通过管子从高电位电极到低电位电极,这些管子内的J线既不终止又不起始。E线形成同样的管子,但或者终止或者起始于不成对电荷与极化电荷的和。这些电荷密度的和是dive-E,它可以由式(6)确定。- E0J.2gP+P,-VE--E..(16)在突然的不连续处,面电荷密度的和确定 E的法向不连续性。考虑到式(9),O.+o,=n.(cE*-.E)=nE(1-g)(17)注意e的分布在使E线成形时不起作用。在图 7.2.3a的均匀导体中,从高电位沿着典型的电流管到低电位时,没有碰到电导率梯度,所以式(6)告诉我们不存在E的源。从而,在整个均勾导体中@满足拉普拉斯方程是不奇怪的在沿着电流管通过图7.2.3b的不连续处时,从低电导率到高电导率,式(17)表明存在E的负值而电荷源。因此,E趋向于从较导电的区域中被排除而在导电较差的区域中塔加。当电导率在如图 7. 2. 3 ℃ 所示 E 的方向平滑地增加时,E-Vo 是正的。 因此,E 的源是负的,而E线沿着通量管减少通常碰到的是均勾和分块均勾的导体,这一类的例子将在7.4和7.5两节中讨论。电导率是平滑地分布的例子类似于6.7 节中示例的平滑地变化的介电常数的情况。在简单的一维构型中,下面的例子说明所有三种类型。例 7.2.1、一维电阻器图 7. 2. 4 所示的电阻器在任何 2一多平面有相同的截面积 4。 沿它的长度4 有电导率 α(1)。完纯导电电极把0处的电位约束为,处的电位约束为零。圆柱形导体被完纯绝缘体包国。馥定电位只和1有关。因此,电场和电流密度是1方向的,并且,没有垂直于绝练边界E的分盘这一条件是自动斑满足的。对于一维场,式(4)简化为(od)0(18)括号中的量即电流密度的负值,在电阻器的整个长度上是不变的。 这样,当小。定义为需数时,ode--.(19)现在将这个表达式从下南的电极到任意位置积分darsTedy(20)02-500在多一比和Φ一处计算这个表达式,就使电流密度与端电压相联系。-J.e./1o(21)· 196
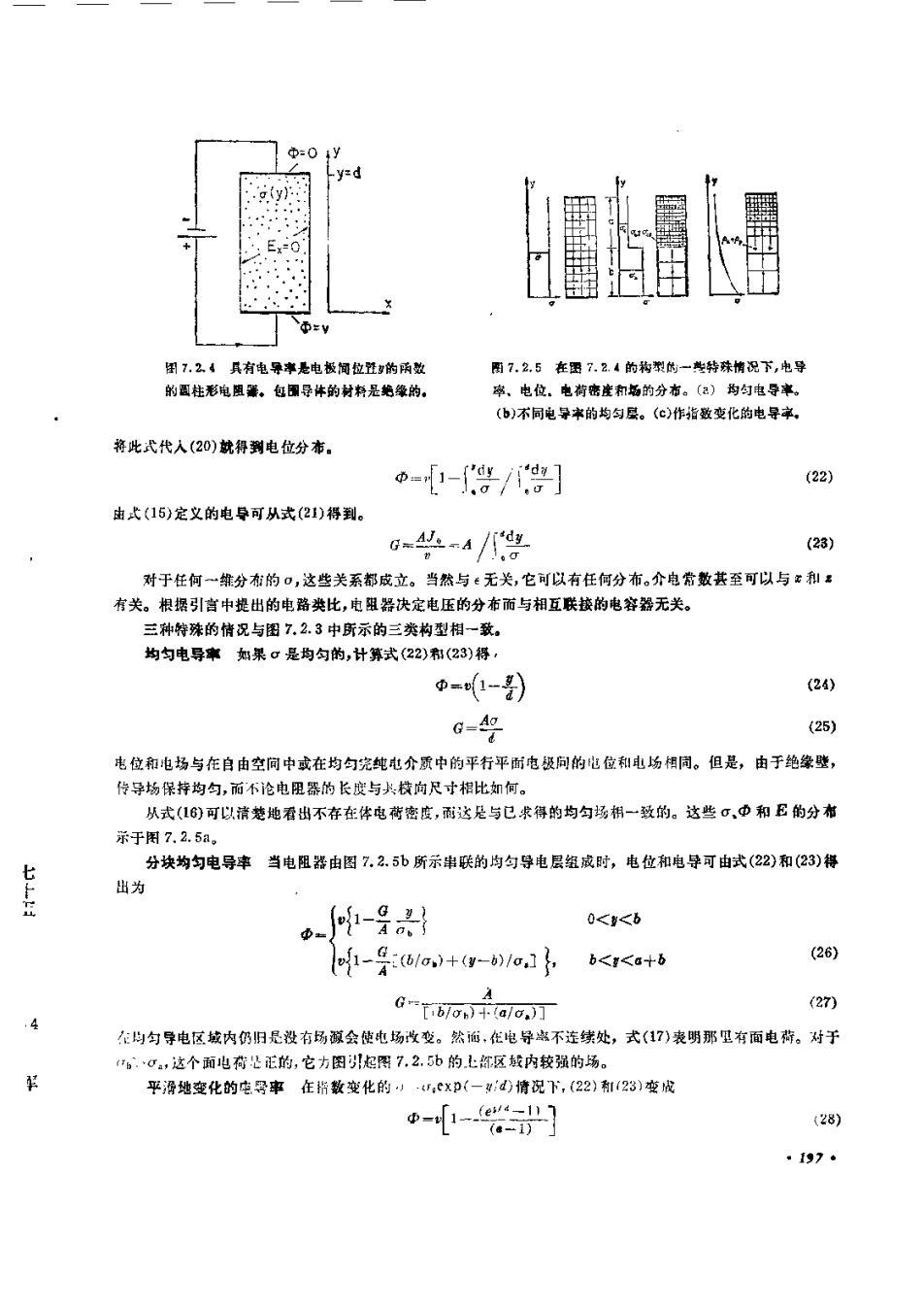
围 7. 2. 4 具有电导率是电极间位经势的两数图 7. 2. 5 在围 7.2. 4 的移型的一些转殊情况下,电导率、电位、电荷密度和场的分布。(a)均幻电导率。的圆柱形电阻骤。包圖导体的材料是绝缘的。(b)不同电导本的均勾层。(c)作指数变化的电导将此式代人(20)就得到电位分布。[1-{% /%](22)由式(15)定义的电导可从式(21)得到G-Afes/'dy(23)对于任何一维分布的0,这些关系都成立。当然与无关,它可以有任何分布。介电常数甚至可以与和z有关。根据引言中提出的电路类比,电阻器决定电压的分布而与相互联接的电容器无关。三种特殊的情况与图7.2.3中所示的三类构型相一致。均匀电导率 如果α 是均勾的,计算式(22)和(23)得,(24)$=e(1-)G-Ao(25)电位和电场与在自由空间中或在均匀究纯电介质中的平行平面电极问的电位和电场相同。但是,由于绝缘璧,传导场保持均匀,而不论电阻器的长度与其核向尺寸相比如何。从式(16)可以清慈地看出不存在体电荷密度,而这是与已崇得的均勾场相一致的。这些6,Φ和E的分布亲于图 7. 2. 5a分块均匀电导率当电阻器由图7.2.5b所示串联的均勾导电层纽减时,电位和电导可由式(22)和(23)得t出为Jl-%?0<<b5(26)(0f1-%:(0/0)+(9-6)/0.1 /b<<a+b(27)[.b/0)-(a/)]在均勺导电区域内仍归是设有场源会使电场改变。然猫,在电导离不连续处,式(17)表明那里有面电荷。对于0,这个面电荷是正的,它力图引起图7.2.5b的L部区毅内较强的场。平滑地变化的电号率在指数变化的4,exp(—3:d)情况下,(22)和(23)变成@-[1--(e-1)(28)197

(29)a(a)这里叫起E的分布的电荷密度由式(16)因此,电场从下部区域被作指数增加的体电荷密度所屏崴7.3分布的电流源和相关的场在稳定条件下,电荷守恒要求电流密度是无散的。因此,J线无始无终。迄今我们认为电流管是起始于所关心的区域的外部,即在边界上。有时引入规定为s(r,t)A/m的体分布的电流源是方便的,从而稳定的电荷守恒方程变成(1)f, J.da=f,sdvvJ=s当我们现作定义了奇异源并考虑它们怎样能够物理地实现时,引人分布的电流源的动机就变得清楚了。分布电流源的奇异性式(1)和高斯定律之间的相似性要求点,线和面电流源的定义如图7.3.1所描述。回到1.3节,那里规定了类似的奇异电荷分布时,应该记住我们现在考虑的是电流密度源,不是电通量源。点电流源引起流出体积的净电流,此体积收缩到零,然而始终包围着源。(e))()图7.3.1上面一行概念性地表示奇异的电流源分布,下面一行提出它们如何可以通过绝缘导线馈电的电极物理地实现f,Jda=i, i,= lm Jsdo(2)im100- 198