
线性代数第二节高斯消元法与矩阵的初等变换初等变换与高斯消元法二:例1考虑方程组的如下解变换2x+X2-x=10ae+x,=-2ix+x=-2ix-20aelR2x+x-x,=1ix+x=-220aelRX2-3x,=51e0C得一般解(无穷多组解)(行(简化)阶梯形矩阵)=-2ix自由未知量X2=3x+5高等教出社新时代大学教学集列教材
第二节 高斯消元法与矩阵的初等变换 新时代大学数学系列教材 线性代数 例1 考虑方程组的如下同解变换: 得一般解(无穷多组解): (行(简化)阶梯形矩阵) 自由未知量 二、初等变换与高斯消元法

线性代数第二节高斯消元法与矩阵的初等变换例2若某方程组经同解变换化为ix-2x-x=1ael-1X2-X=-11YOARX=50有唯一解显然,(行阶梯形矩阵)例3若某方程组经同解变换化为X - 2x2 - x, =1ael01DARX2-x=-1On90X2-X=5OX-2x2-X=1ael8即CoRX2-x=-11oSe000=6O无解高等教出社显然,经1新时代大学数学集列教材
第二节 高斯消元法与矩阵的初等变换 新时代大学数学系列教材 线性代数 例2 若某方程组经同解变换化为 显然,有唯一解. (行阶梯形矩阵) 例3 若某方程组经同解变换化为 显然,无解. 即
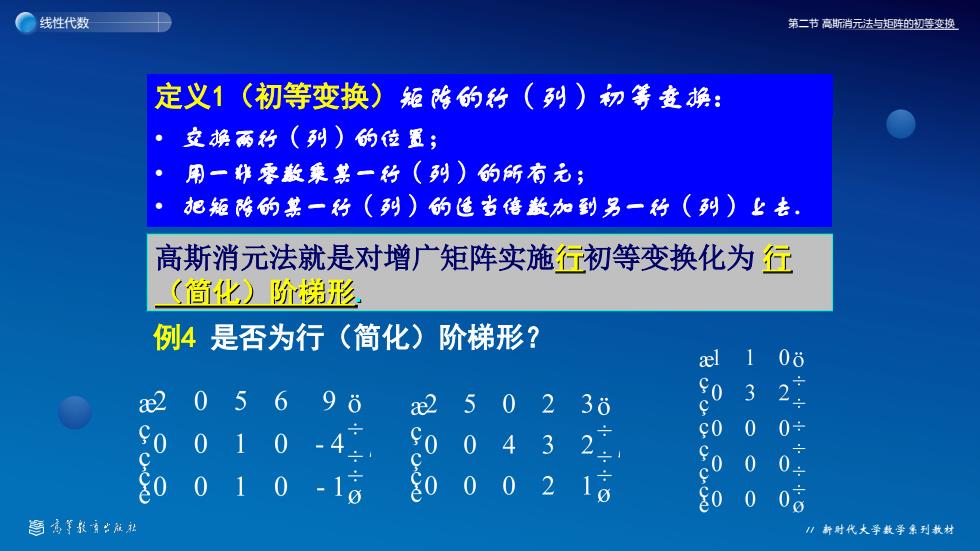
线性代数第二节高斯消元法与矩阵的初等变换定义1(初等变换)短降的行(列)初等变换:交换两行(列)的位置;用一排零数乘某一行(列)的所有元;把短陷的某一行(列)的适当倍数加到另一行(列)上去高斯消元法就是对增广矩阵实施行初等变换化为行(简化)阶梯形阶梯形?例4是否为行(简化)00ael0032h30aeRS00:00.o+0中00高等教出社1新时代大学数学集列教材
第二节 高斯消元法与矩阵的初等变换 新时代大学数学系列教材 线性代数 定义1(初等变换)矩阵的行(列)初等变换: • 交换两行(列)的位置; • 用一非零数乘某一行(列)的所有元; • 把矩阵的某一行(列)的适当倍数加到另一行(列)上去. 高斯消元法就是对增广矩阵实施行初等变换化为 行 (简化)阶梯形. 例4 是否为行(简化)阶梯形?