
3.4一阶动态电路的响应 二、零状态响应 二、零状态响应 定义:当电路的初始储能为零(即初始状态 为零)时,仅由外加激励所引起的响应,称 R 为零状态响应,记为y()。 例:电路如图(a)所示,已知t<0时,开关S是闭合,电路已达稳态。在t= 0时,开关S断开,求≥0时,电容电压uc()(注意:该响应为零状态响应, 为何?)。 解:所求响应为零状态响应。≥0时,根据KCL有i心+=s 由于ic=C duc/dt,iR=ucR,代入上式得 duc 1 1 +-uc 式中=RC,初始值uc(0)=0 dtπ uc(t)uch(t)ucp(t) 对应的齐次解为uc,(t)=Ket 6
6 二、零状态响应 定义:当电路的初始储能为零(即初始状态 为零)时,仅由外加激励所引起的响应,称 为零状态响应,记为yzs(t)。 例:电路如图(a)所示,已知t < 0时,开关S是闭合,电路已达稳态。在t = 0时,开关S断开,求t≥0时,电容电压uC(t) (注意:该响应为零状态响应, 为何?)。 解: 所求响应为零状态响应。t≥0时,根据KCL有 iC + iR = Is 由于 iC= C duC/dt, iR = uC/R,代入上式得 C S C I C u t u 1 1 d d + = 式中τ=RC,初始值uC(0+ ) = 0 uC(t) = uCh(t) + uCp(t) 对应的齐次解为 t uCh t K − ( ) = e S uC IS iC iR C R 3.4 一阶动态电路的响应 二、零状态响应
3.4一阶动态电路的响应 二、零状态响应 其特解为常数,令uCp)=A,将其代入微分方程得 故得特解uc(①)=RIs 完全解为uc(t)=Ket+RIs 将初始状态uc04)=0代入确定K,有uc(0),=K+Rs,解得K=-RIs 于是得电路的零状态响应uc)=Rs(I-eT),t≥0 物理 过程: 电容电流 ie-Cduc -lye ic◆uc 充电 dt IsR 电容充电,当t→时,达到稳定状态,其稳态 值uc(o)=Rs。而电容电流i按指数规律衰减, 当达到稳态时,ic(o)=0。 零状态响应满足齐次性。若有多个激励,零状态响应与各激励之 间也满足可加性。这种性质称为零状态线性
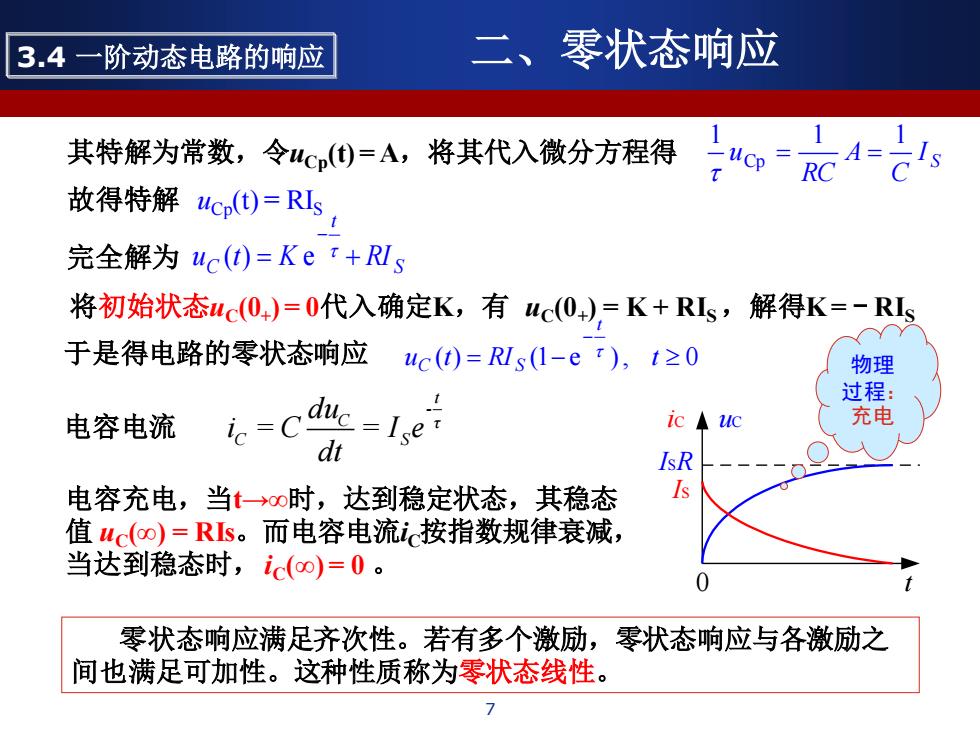
7 其特解为常数,令uCp(t) = A,将其代入微分方程得 S I C A RC u 1 1 1 Cp = = 故得特解 uCp(t) = RIS 完全解为 S t uC t = K + RI − ( ) e 将初始状态uC(0+ ) = 0代入确定K,有 uC(0+ ) = K + RIS ,解得K = - RIS 于是得电路的零状态响应 ( ) = (1− e ), 0 − u t RI t t C S iC uC ISR IS 0 t 电容电流 t - C τ C S du i = C = I e dt 电容充电,当t→∞时,达到稳定状态,其稳态 值 uC(∞) = RIs。而电容电流iC按指数规律衰减, 当达到稳态时,iC(∞) = 0 。 零状态响应满足齐次性。若有多个激励,零状态响应与各激励之 间也满足可加性。这种性质称为零状态线性。 物理 过程: 充电 3.4 一阶动态电路的响应 二、零状态响应