2.7 等效电源定理 一、 等效电源定理 1、戴维南定理:任意一个线性二端含源电路,对其外部 而言,可以用一个电压源和电阻的串联组合来等效。 开 a 路 任意 N Woc 二端 任何 可等效为2uoc 任何 线性 u 外接 外接 6 Ro 电路N 电路 电路 a 含源 No 戴维南等效电 所有独立源为 b 路 零值 戴维南等效内阻
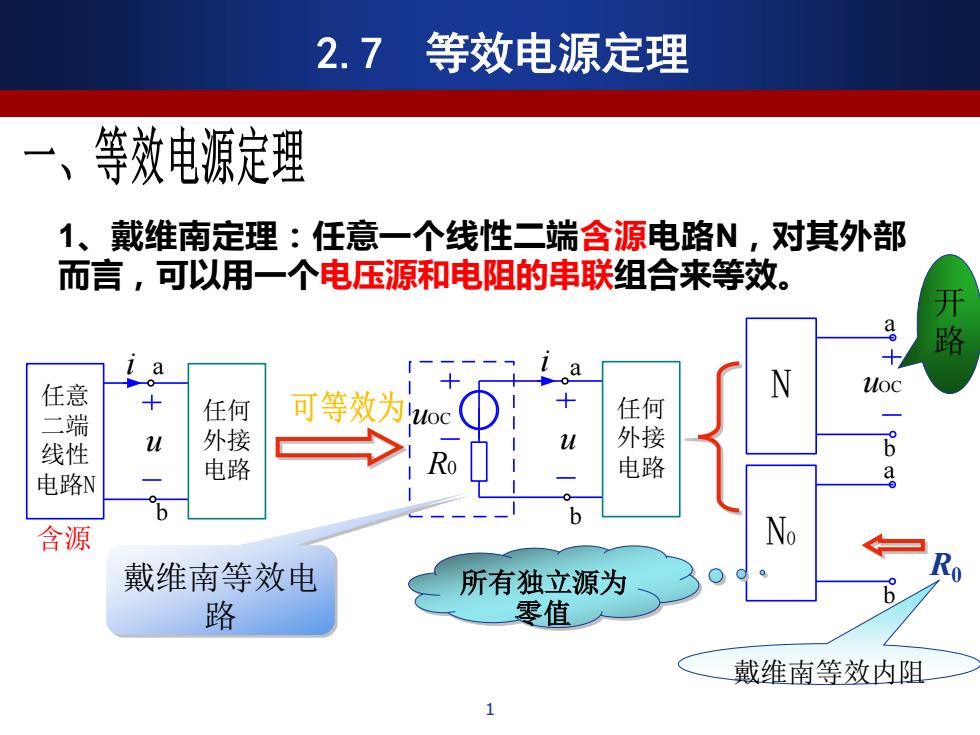
u 任意 二端 线性 电路N 任何 外接 电路 i a b b u 任何 外接 电路 i uOC R0 a N uOC a b N0 a b 所有独立源为 R0 零值 开 路 戴维南等效电 路 戴维南等效内阻 1、戴维南定理:任意一个线性二端含源电路N,对其外部 而言,可以用一个电压源和电阻的串联组合来等效。 2.7 等效电源定理 1 含源

2.7等效电源定理 三、戴维南等效内阻的计算★ ·1、对无受控源的二端电路N一串并联方法 若二端电路N中无受控源,当令N中所有独立源的值为 零(电压源短路,电流源开路)后,而得到的N是一个纯 电阻电路。此时,利用电阻的串并联公式和Y-△等效公式 求R最简单。 2
2 2.7 等效电源定理 三、戴维南等效内阻的计算★ ❖1、对无受控源的二端电路N——串并联方法 若二端电路N中无受控源,当令N中所有独立源的值为 零(电压源短路,电流源开路)后,而得到的N0是一个纯 电阻电路。此时,利用电阻的串并联公式和Y-△等效公式 求R0最简单
2.7等效电源定理 三、戴维南等效内阻的计算★ ·2、对于含受控源的二端电路N 冬(1)外加电源法★ 所有独立源的值为零(电压源短路,电流源开路); 保留受控源; No u Ro No No (a)外加电压源法 (b)外加电流源法 u与i对N一定要取 关联方向呦】
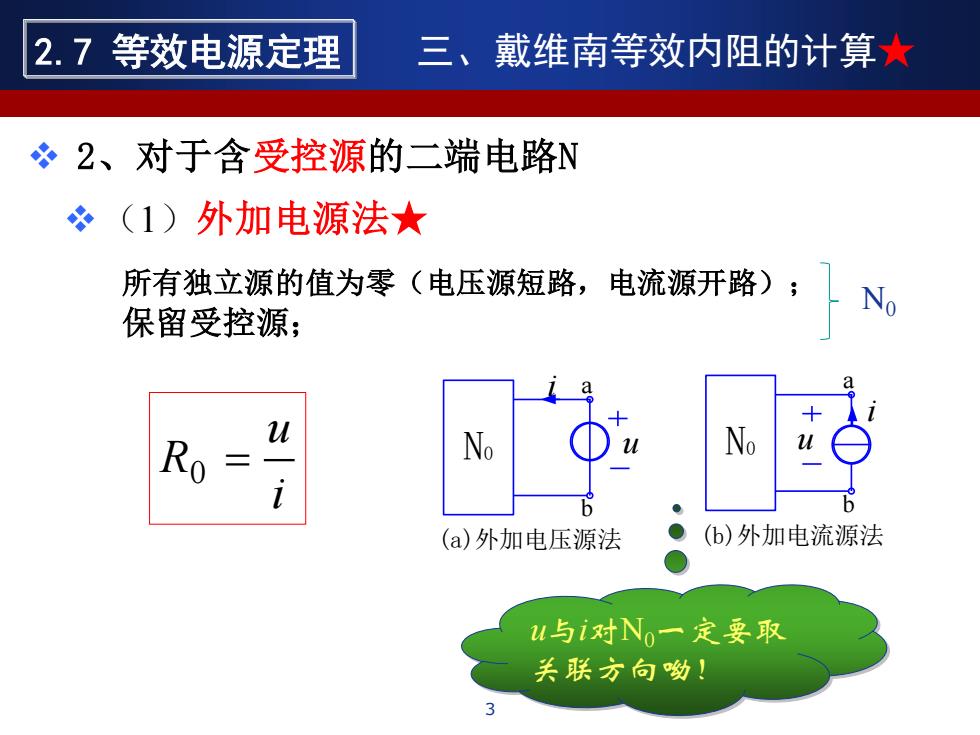
所有独立源的值为零(电压源短路,电流源开路); 保留受控源; N0 u a b i (a)外加电压源法 N0 u a b i (b)外加电流源法 i u R0 = u与i对N0一定要取 关联方向呦! ❖(1)外加电源法★ ❖ 2、对于含受控源的二端电路N 3 2.7 等效电源定理 三、戴维南等效内阻的计算★ N0

2.7等效电源定理 三、戴维南等效内阻的计算★ (2)开路短路法 先求出oc,再求出isc(注意:若求uoc时其参考 方向a为“+”极,则求isc时其参考方向应设成从a 流向b),则 R0= uoc isc
先求出uOC,再求出iSC(注意:若求uOC时其参考 方向a为“+”极,则求iSC时其参考方向应设成从a 流向b),则 ❖ (2)开路短路法 4 SC OC i u R0 = 2.7 等效电源定理 三、戴维南等效内阻的计算★

2.7等效电源定理 三、戴维南等效内阻的计算★ ,(3)伏安关系法 戴维南等效电路如图(a),端口上电压u与电 流取关联参考方向,其端口的伏安关系(VAR) 为 u=uoc RoI 拓展:非关联(将i反向)u=uoc-R,I (a) 所谓伏安关系法就是直接对二端线性电路N,推导出两端子 上的电压和电流之间的一次关系式,其常数项即为开路电压 4oc,电流前面所乘的系数即为等效内阻R,。 思考:若未接入外电路,电流=0,u=uoc,无法测内阻,方法失效」 因此,若要使用伏安关系法,必须接入外电路。最简单方法:外接激励源!
戴维南等效电路如图(a),端口上电压u与电 流i取关联参考方向,其端口的伏安关系(VAR) 为 u = uOC + R0 I 拓展:非关联(将i反向) u = uOC - R0 I b u (a) i R0 a uOC 所谓伏安关系法就是直接对二端线性电路N,推导出两端子 上的电压u和电流i之间的一次关系式,其常数项即为开路电压 uOC ,电流前面所乘的系数即为等效内阻R0 。 ❖ (3)伏安关系法 5 2.7 等效电源定理 三、戴维南等效内阻的计算★ 思考:若未接入外电路,电流i=0,u=uOC,无法测内阻,方法失效! 因此,若要使用伏安关系法,必须接入外电路。最简单方法:外接激励源!