
知识点回顾 1.正弦量的相量形式 i(t)=Im cos(wt +j) 2.引入相量法的意义? ·将同频正弦量加减的运算转化为复数加减运算 运算方法:(1)准确计算一复数运算法则; (2)定性 分析——图解法 。 将正弦量的微积分运算转化为乘除运算 dt i()dt←
知识点回顾 1. 正弦量的相量形式 ( ) cos( ) m i i t I t = + w j , 2 m i m m i I I I I & & = ? ? j j 2. 引入相量法的意义? • 将同频正弦量加减的运算转化为复数加减运算 运算方法:(1)准确计算——复数运算法则;(2)定性 分析——图解法 • 将正弦量的微积分运算转化为乘除运算 j I d t d i t → ( ) → j I i t d t ( )

知识点回顾 3.相量法的适用范围? 同频率正弦激励的线性时不变稳态电路 4.基尔霍夫定律的相量形式 ∑i0=0 ∑i=0 ∑()=0 ∑U=0 5.元件VAR的相量形式 有效值关系:URRI UR=RI∠0,=Ri L相位关系:pwp 0.=oL1∠(g+=joLd 有效值关系:U=oLl 相位关系:0=0+90°
知识点回顾 3. 相量法的适用范围? 同频率正弦激励的线性时不变稳态电路 4. 基尔霍夫定律的相量形式 = = = = ( ) 0 0 ( ) 0 0 u t U i t I 5. 元件VAR的相量形式 U R R R i = = I I 有效值关系:UR= RI 相位关系: u= π ( ) 2 L i U L L = + = I I j 有效值关系:UL = L I 相位关系: u= i +90°
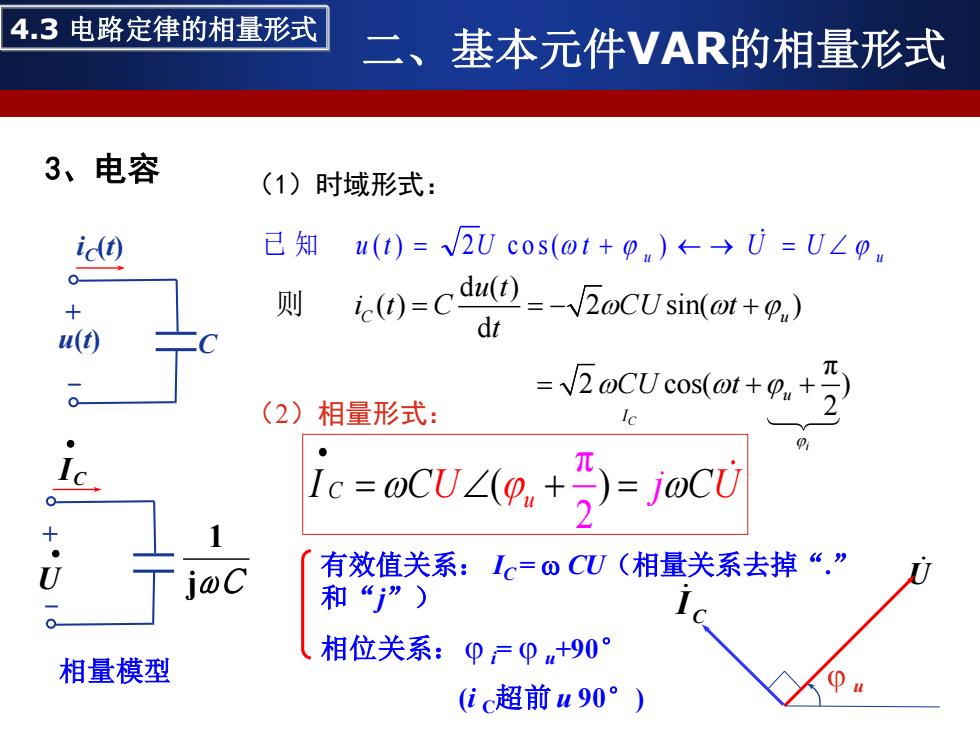
4.3电路定律的相量形式 二、基本元件VAR的相量形式 3、电容 (1)时域形式: 已知 u()=√2Ucos(o1+pm)←→U=ULpm 则 ic()=cdu(D-oCUsin(+) dt -CUcs+ (2)相量形式: ic=@CUL(@.+)=jwCU i@c 有效值关系:Ic=0CU(相量关系去掉“.” 和“”) 相量模型 相位关系:0,=0+90° (ic超前u90°)
3、电容 (1)时域形式: (2)相量形式: ( π 2 C ) u I C C U j U • = + = u U U u 已 知 u (t ) = 2U c o s ( t + ) → = d ( ) ( ) 2 sin( ) d π 2 cos( ) 2 C i C u u I u t i t C CU t t CU t = = − + = + + 则 相量模型 有效值关系: IC = CU(相量关系去掉“.” 和“j”) 相位关系: i= u+90° (i C超前 u 90°) U C I u iC (t) u(t) C + - • U I C • + - jωC 1 二、基本元件VAR的相量形式 4.3 电路定律的相量形式

4.3电路定律的相量形式 二、 基本元件VAR的相量形式 (3) 容抗与容纳:0=ie/joC 令Xc=1/(oC),称为容抗,单位为2(欧姆) Bc=QC,称为容纳,单位为S 电容VAR的相量形式: 0:xi=-71=,1=B0=u @C 容抗与频率成反比,。→0,Xc→∞直流开路 0→0,Xc→0高频短路 (4)功率:k0=c0-2 oCUsin(@+-n) dt Pc =uic=-2Ulc cos+)sin+Xc =-UIc sin2(@t+) @t 瞬时功率以20交变,有正有 负,一周期内刚好互相抵消
(3)容抗与容纳: 令XC = 1/(ωC),称为容抗,单位为Ω(欧姆) B C = ω C, 称为容纳,单位为S 容抗与频率成反比, ω → 0, XC → 直流开路 ω → ,XC→ 0 高频短路 XC (4)功率: sin 2( ) 2 c o s( ) sin( ) C u C C C u u U I ω t p u i U I ω t ω t = − + = = − + + t iC O u pC 2 瞬时功率以2交变,有正有 负,一周期内刚好互相抵消。 电容VAR的相量形式: 1 1 , U jX I j I I I jB U j CU C C C C C C C j C = − = − = = = 二、基本元件VAR的相量形式 4.3 电路定律的相量形式 / U I j C = C d ( ) ( ) 2 sin( ) d C u u t i t C CU t t = = − +
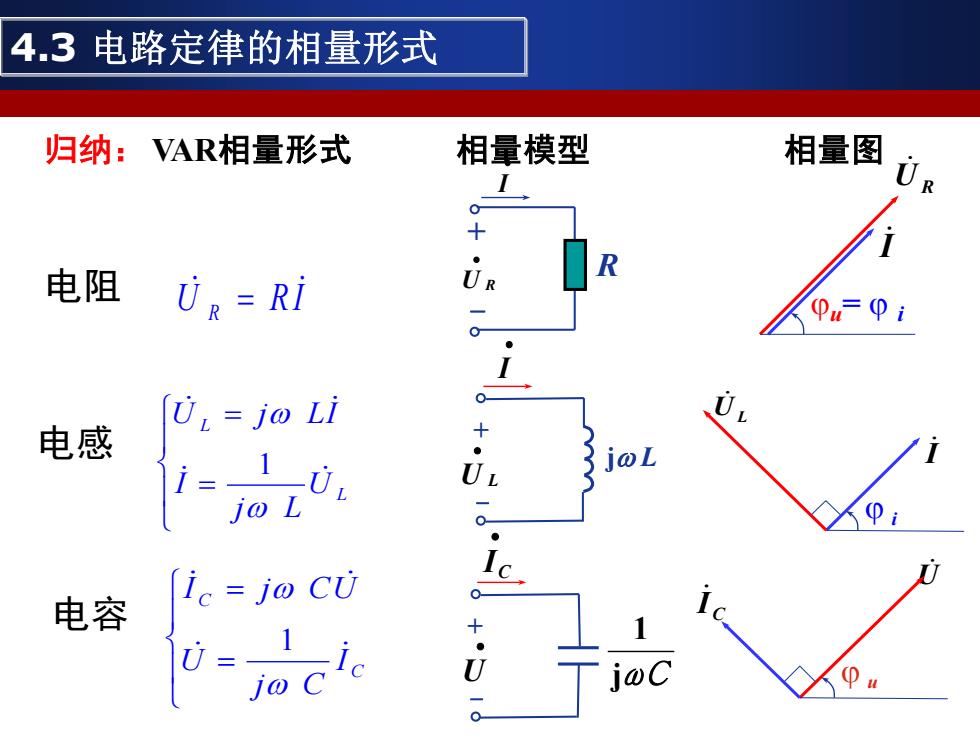
4.3电路定律的相量形式 归纳:VAR相量形式 相量模型 相量图 电阻 Un=Ri U=jo Li 电感 电容 ic=j@CU i00 u
归纳: VAR相量形式 相量模型 相量图 电阻 U R I R = R + - U R • • I UR I u= i 电感 = = L L U j L I U j LI 1 j L + - U L • • I UL I i 电容 = = C C I j C U I j CU 1 • U I C • + - jωC 1 U C I u 4.3 电路定律的相量形式