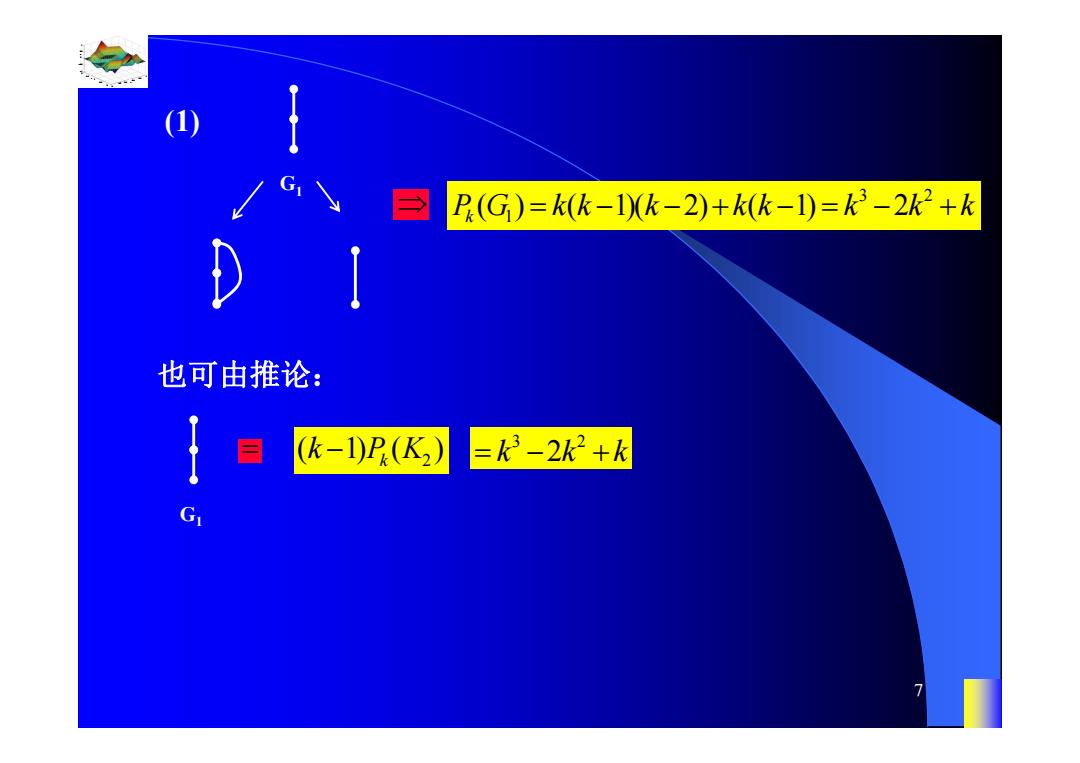
(1 P.(G)=k(k-1k-2)+k(k-1)=k3-2k2+k 也可由推论: (k-1)P(K) =K-2K2+k G
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 (1) G1 3 2 1 Pk ( ) ( 1)( 2) ( 1) 2 G kk k kk k k k 也可由推论: G1 2 ( 1) ( ) k k PK 3 2 k kk 2
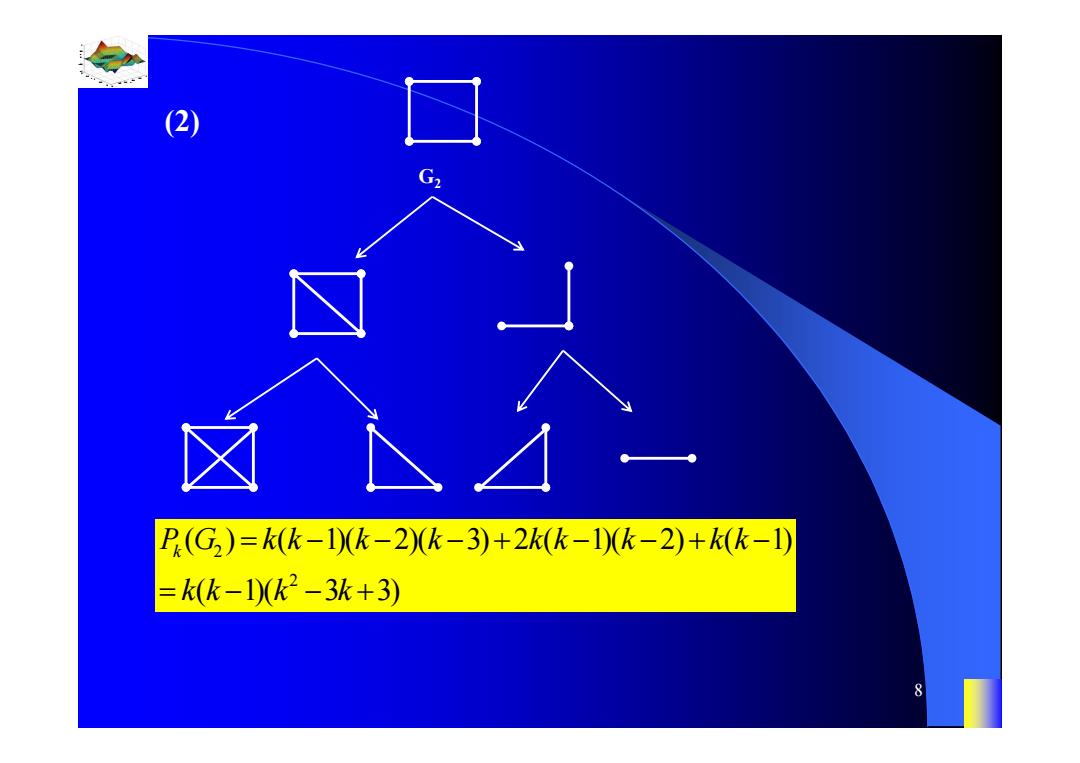
(2) P.(G2)=k(k-1(k-2k-3)+2k(k-1k-2)+k(k-1) =k(k-1)K2-3k+3) 8
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 (2) G2 2 2 ( ) ( 1)( 2)( 3) 2 ( 1)( 2) ( 1) ( 1)( 3 3) PG kk k k kk k kk k kk k k
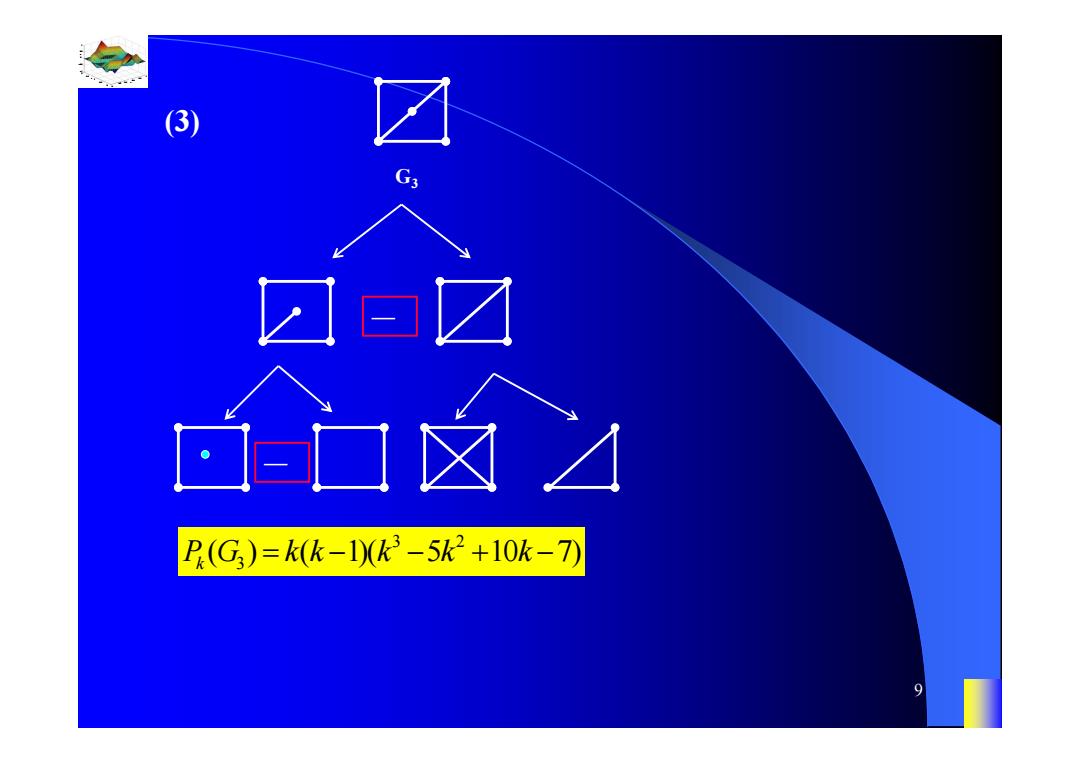
之 (3) G3 ☒ P.(G)=k(k-1k3-5k2+10k-7 9
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 (3) G3 — — 3 2 3 ( ) ( 1)( 5 10 7) PG kk k k k k

注:递推计数法的计算复杂度是指数型的。 2、理想子图计数法 (1)预备知识 定义1:设H是图G的生成子图。若H的每个分支均为 完全图,则称H是G的一个理想子图。用N,(G)表示G的 具有r个分支的理想子图的个数。 例2求N(G),N(G)。 10
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 注:递推计数法的计算复杂度是指数型的。 2、理想子图计数法 (1) 预备知识 定义1:设H是图G的生成子图。若H的每个分支均为 完全图,则称H是G的一个理想子图。用N r (G)表示G的 具有 r 个分支的理想子图的个数。 例2 求N4(G), N5(G)。 G
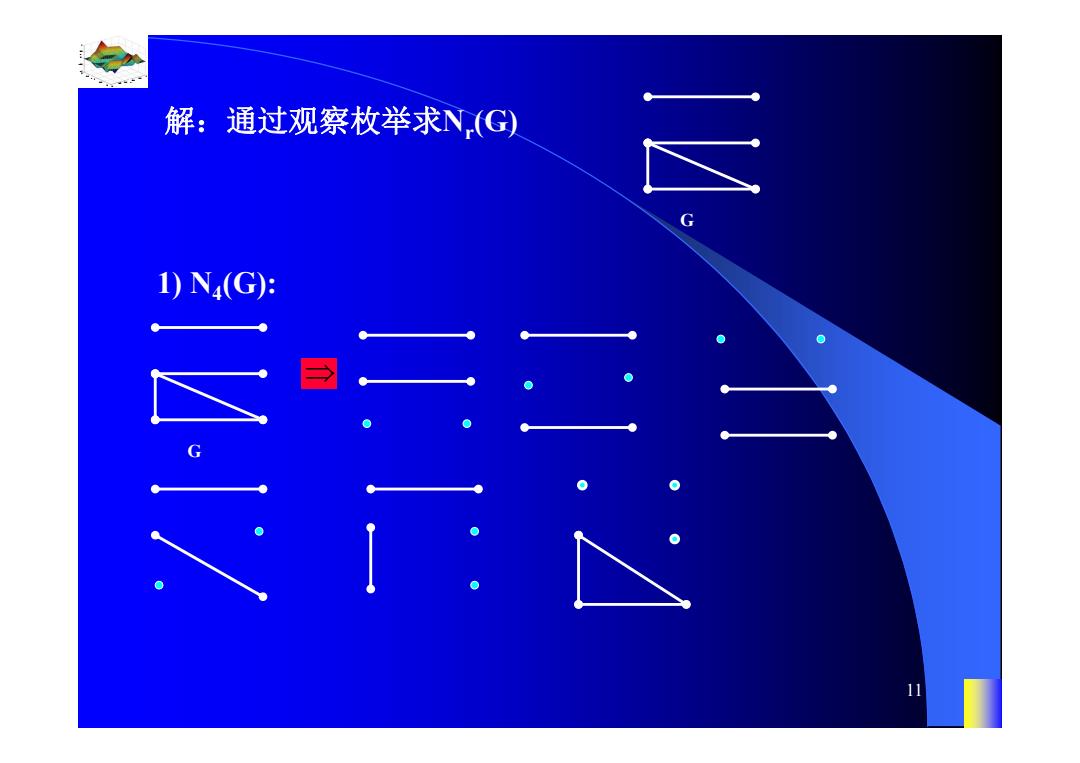
解:通过观察枚举求N(G) 三 1)N4(G): 11
0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 解:通过观察枚举求Nr(G) G 1) N4(G): G