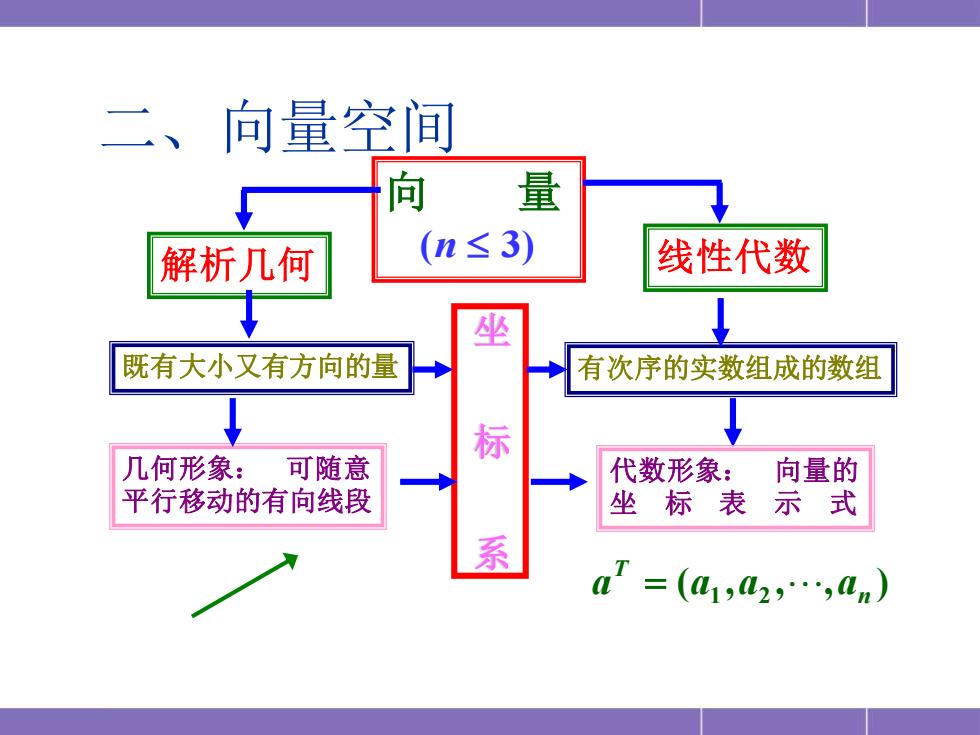
二、向量空间 向 量 解析几何 (n≤3) 线性代数 既有大小又有方向的量 有次序的实数组成的数组 标 几何形象: 可随意 代数形象: 向量的 平行移动的有向线段 坐标表 示式 =(a132,.3n)
向 量 (n 3) 解析几何 线性代数 既有大小又有方向的量 有次序的实数组成的数组 几何形象: 可随意 平行移动的有向线段 代数形象: 向量的 坐 标 表 示 式 ( , , , ) 1 2 n T a = a a a 坐 标 系 二、向量空间
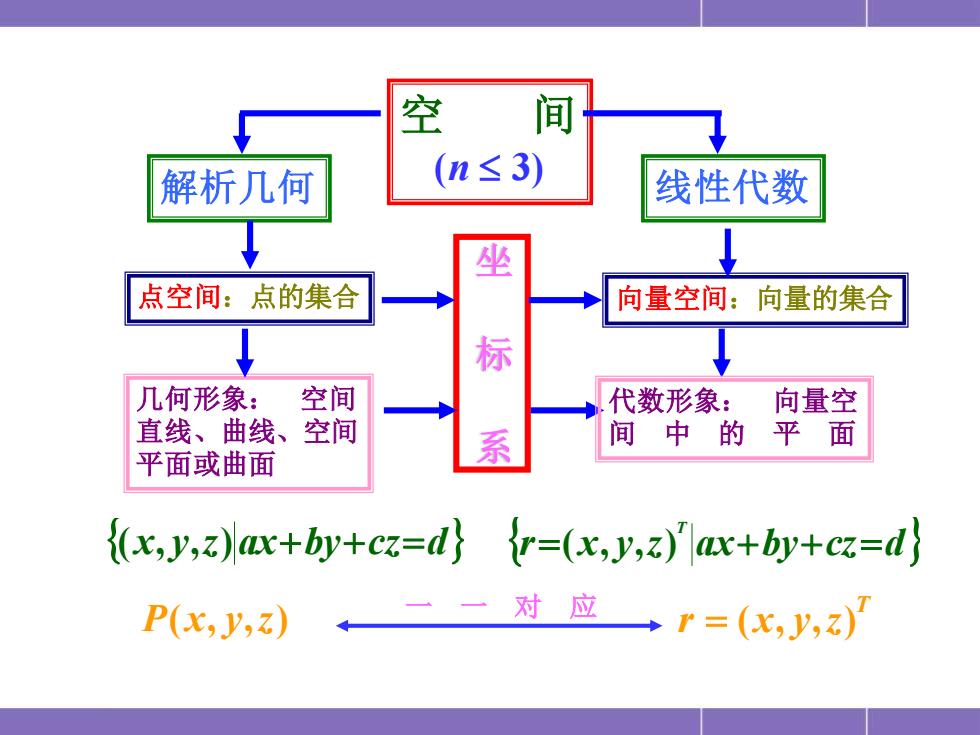
空 间 解析几何 (n≤3) 线性代数 坐 点空间:点的集合 向量空间:向量的集合 ↓ 标 几何形象: 空间 代数形象: 向量空 直线、曲线、空间 系 间中 的 平面 平面或曲面 {(x,y,z)ax+by+cz=d}r=(x,y,z)"ax+by+cz=d P(x,y,z) 一 对应 →r=(x,y,)
空 间 (n 3) 解析几何 线性代数 点空间:点的集合 向量空间:向量的集合 坐 标 系 代数形象: 向量空 间 中 的 平 面 r x y z ax by cz d T =( , , ) + + = 几何形象: 空间 直线、曲线、空间 平面或曲面 (x, y,z)ax+by+cz=d P(x, y,z) r (x, y,z) T = 一 一 对 应

n>3时,n维向量没有直观的几何形象. R={c=(xx2,x)xx,x,eR} 叫做n维向量空间. x==(xnxxx)lax+a:x:+.+a.x.=bj 叫做n维向量空间R”中的n-1维超平面
R x x x xn x x xn R n T = =( 1 , 2 , , ) 1 , 2 , , x x x xn a x a x an xn b T = =( 1 , 2 , , ) 1 1+ 2 2++ = 叫做 n 维向量空间. n 3 时, n 维向量没有直观的几何形象. 叫做 维向量空间 R 中的 维超平面. n n n − 1
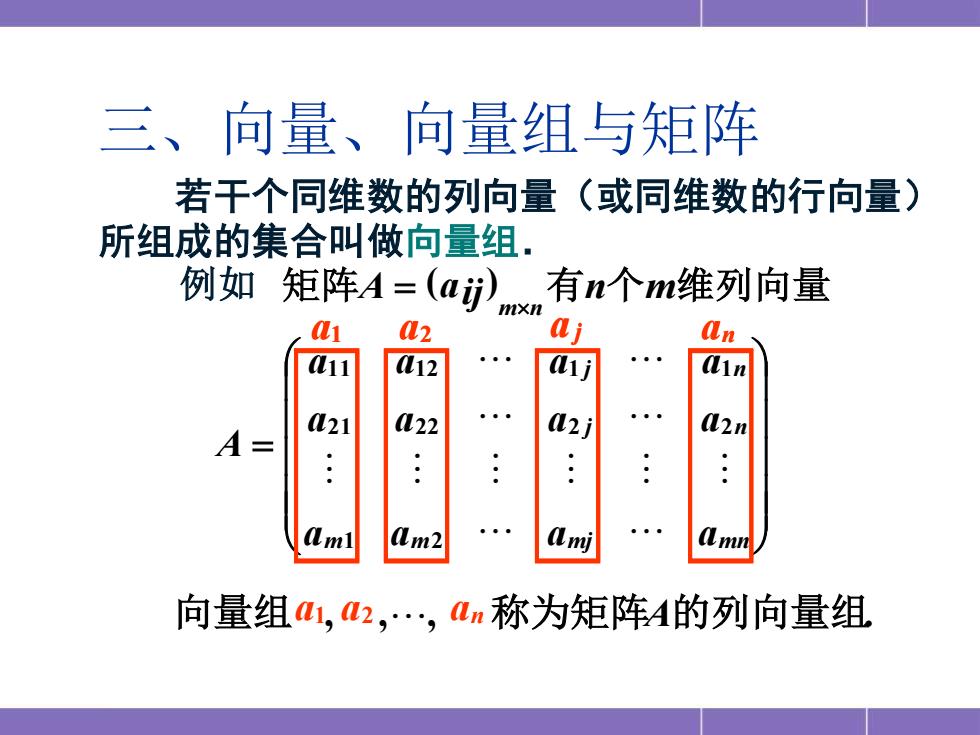
三、向量、向量组与矩阵 若干个同维数的列向量(或同维数的行向量) 所组成的集合叫做向量组 例如 矩阵A=(aj》n有n个m维列向量 02 11 12 01 1n L21 L22 a2j (2n A= am2 L 向量组,2,4n称为矩阵4的列向量组
若干个同维数的列向量(或同维数的行向量) 所组成的集合叫做向量组. 例如 矩阵A = (aij) mn 有n个m维列向量 = a a a a a a a a a a a a A m m mj mn j n j n 1 2 2 1 2 2 2 2 1 1 1 2 1 1 a1 向量组 a1, a2 , , an 称为矩阵A的列向量组. 三、向量、向量组与矩阵 a1 a2 a j an