
三、向量的概念向量:既有大小,又有方向的量称为向量(又称矢量)表示法:有向线段MM,或a.向量的模:向量的大小,记作M,M,或a单位向量:模为1的向量,记作e零向量:模为0的向量,记作0
表示法: 向量的模 : 向量的大小, 三、向量的概念 向量: 既有大小, 又有方向的量称为向量 (又称矢量). 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量, 有向线段 M1 M2 , 或 a

O?三、向量的概念向量相等:如果两个向量和b的大小相等,且方向相同,我们就说向量(和h为相等向量,记作α=b.负向量:与向量α大小相等,方向相反的向量叫作α的负向量(反向量)记作-a.平行:两个非零向量如果它们的方向相同(或者相反),就称这两个向量平行.又称两向量共线.向量a与b平行,记作aPb,零向量与任何向量平行;共面:设有k(k33)个向量,当它们的起点放在同一点时,如果k个终点和公共起点在一个平面上,则称这k个向量共面
三、 向量的概念 12 零向量与任何向量平行 ;

01空间直角坐标系本讲内容02空间两点间的距离03向量的概念向量的线性运算0405向量的坐标06向量的数量积和方向余弦07向量的向量积与混合积
本讲内容 01 空间直角坐标系 02 空间两点间的距离 03 向量的概念 04 向量的线性运算 05 向量的坐标 06 向量的数量积和方向余弦 07 向量的向量积与混合积 04
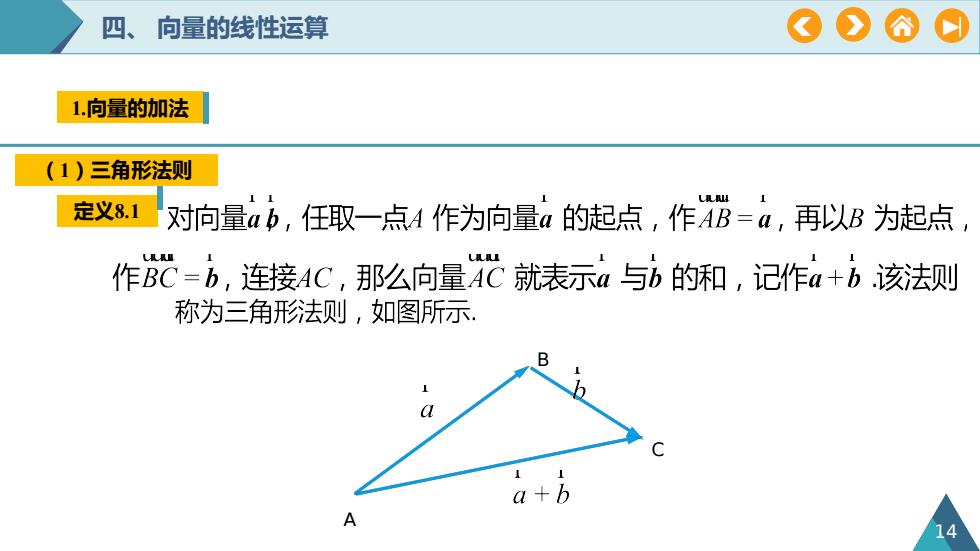
CA四、向量的线性运算1.向量的加法(1)三角形法则定义8.1对向量ab,任取一点A作为向量a的起点,作AB=a,再以B为起点,作BC=b,连接AC,那么向量AC就表示a与b的和,记作a+b.该法则称为三角形法则,如图所示Ba11a+bA14
四、 向量的线性运算 1.向量的加法 定义8.1 14 B C A (1)三角形法则
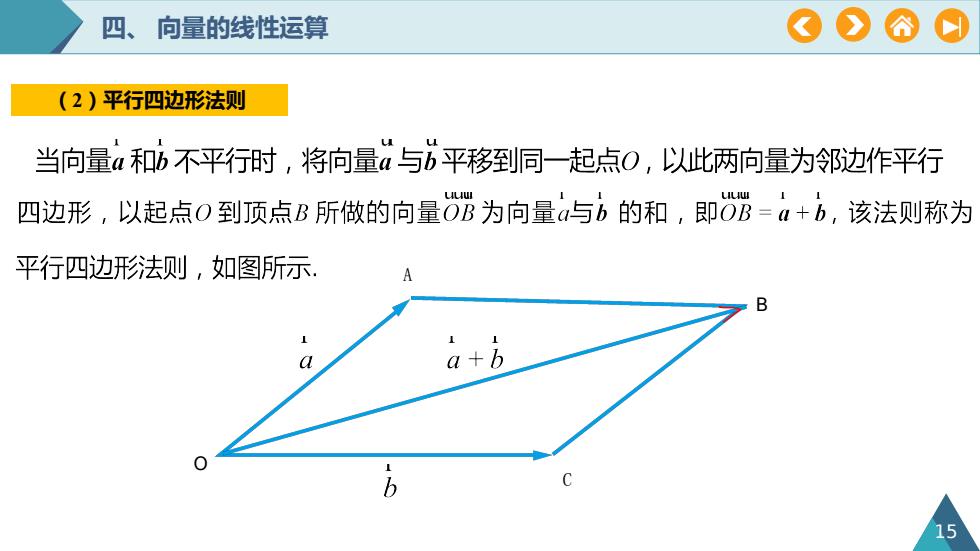
A四、向量的线性运算(2)平行四边形法则当向量a和b不平行时,将向量a与b平移到同一起点O,以此两向量为邻边作平行四边形,以起点O到顶点B所做的向量OB为向量a与b的和,即OB=a+b,该法则称为平行四边形法则,如图所示ABaOb15
四、 向量的线性运算 15 O B A C (2)平行四边形法则