《电磁场与电磁能》课程PPT教学课件（马冰然版）复习题题

：计算A的旋度A的环量等于零。A的旋度也应等于零。axaya.0aaVxAOzaxayx212>2a(22)a(x)a(y)a(y)a(22)a(x?)aOzaxaxayayaz0一练习1-10

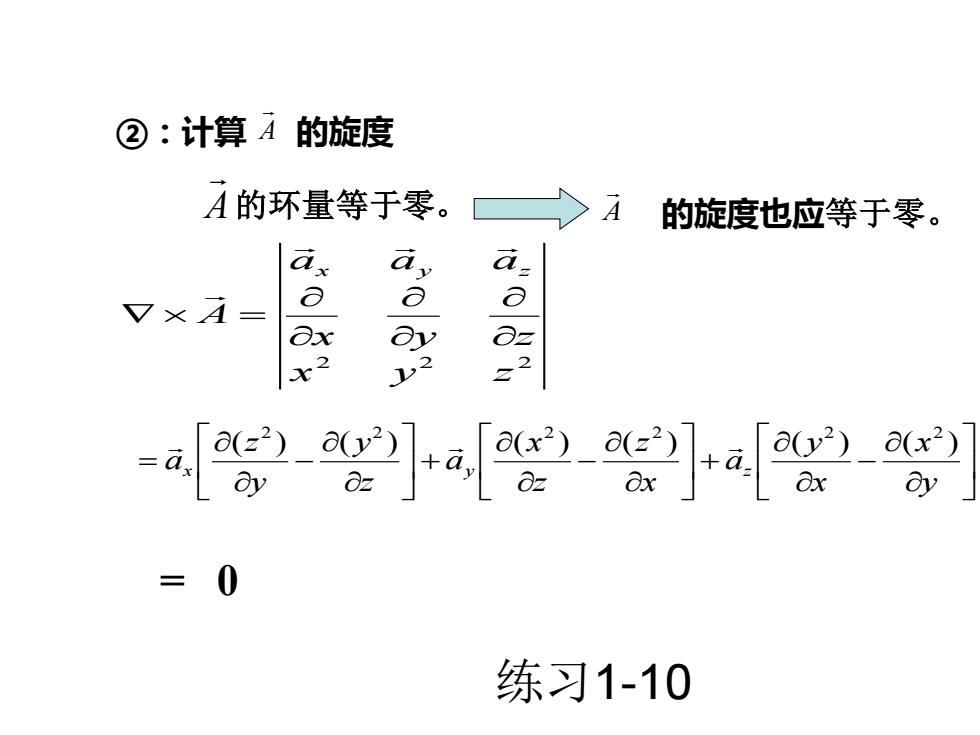
②：计算 A 的旋度  A 的环量等于零。  A 的旋度也应等于零。  2 2 2 x y z x y z a a a A x y z        =             −    +        −    +        −   = y x x y a x z z x a z y y z ax y z ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 2    = 0 练习1-10

2静电场

2 静电场

例：2-1有限长直线L上均匀分布着线密度为p的线电荷,求线外任一点的电场强度.解:采用柱坐标系,并将 z轴与直导线重合，原点在直导线的中点,场点坐标为P(r,ps线电荷元为ed,它在场点的电场强度沿柱坐标系的三个8dE.dE分量为：dE电场方向在源点与场点的连线上。0=p,dzdE,=dE|cos0COsR24元60P,dzdE。=0dE, =dE sin 0sin04元013R22025/6/11

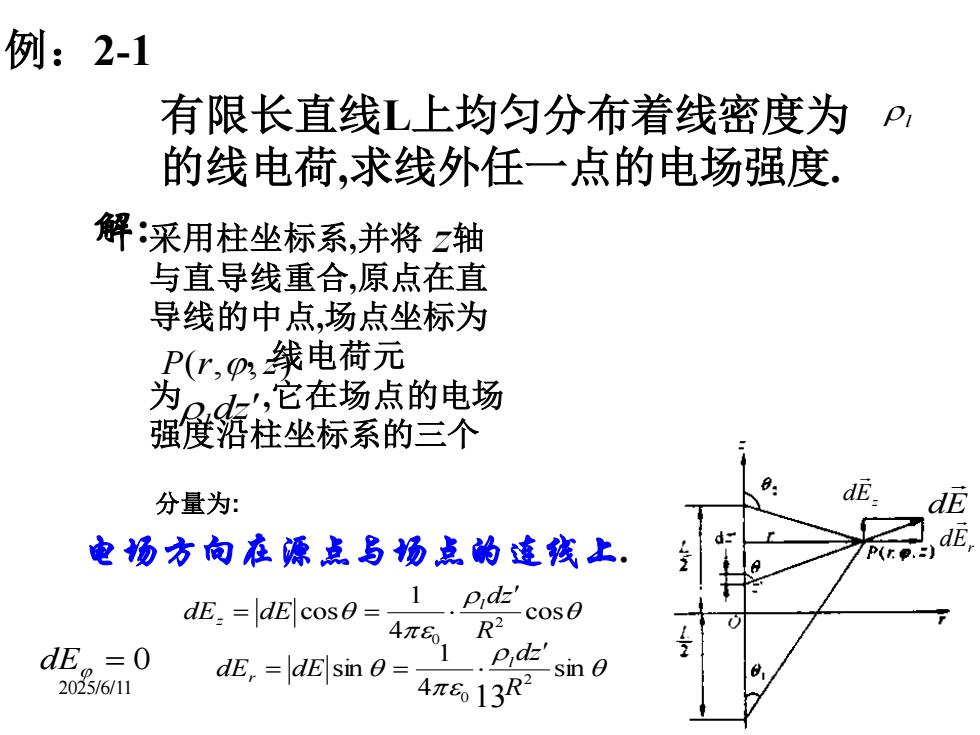
2025/6/11 13 例：2-1 有限长直线L上均匀分布着线密度为 的线电荷,求线外任一点的电场强度.  l Er d  dE  dEz  解: 电场方向在源点与场点的连线上.      sin 4 1 sin 2 0 R dz dE dE l r  dE = 0 = =       cos 4 1 cos 2 0 R dz dE dE l z  = =  采用柱坐标系,并将 轴 与直导线重合,原点在直 导线的中点,场点坐标为 , 线电荷元 为 ,它在场点的电场 强度沿柱坐标系的三个 P(r,,z) dz l   z 分量为:

YR =.=rcscasin 08.dE.dEz'= z-rcot0dE即dz'=rcsc2doP(r,Φ,2)R1P,r cscedoZ.. dE,sin 4元8r? csc2卡1p, sin dde4元11Pr csc dedEcosOr? csc? 4元81P, cos edo4元80r2025/6/1114

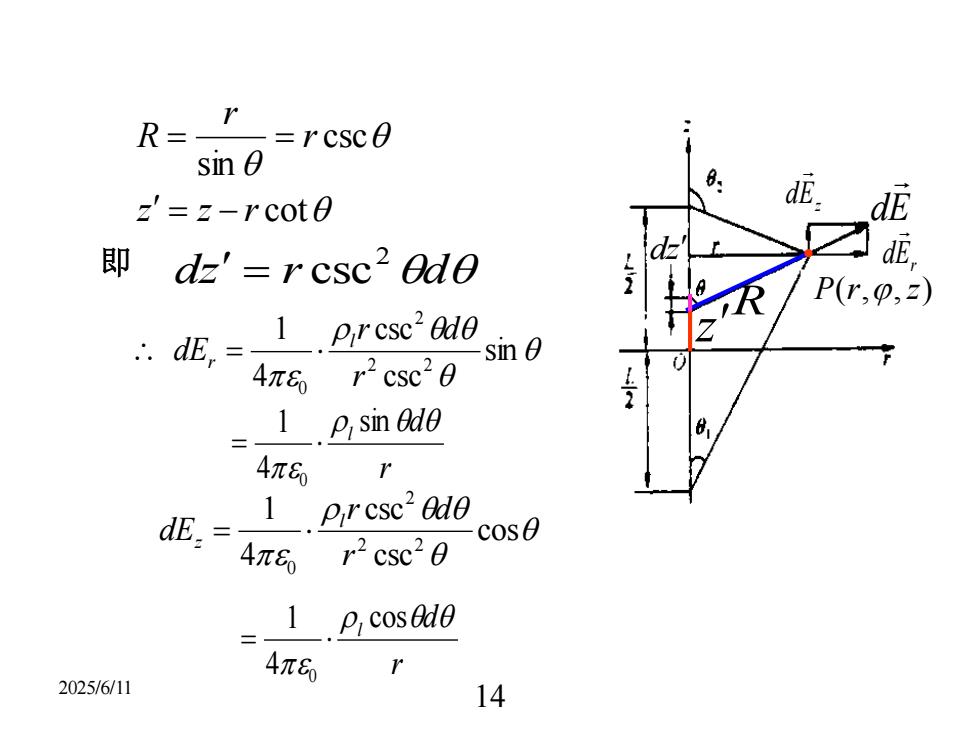
2025/6/11 14    cot csc sin z z r r r R  = − = = dz r d 2 即  = csc        sin csc csc 4 1 2 2 2 0 r r d dE l r  =  r d l      sin 4 1 0 =         cos csc csc 4 1 2 2 2 0 r r d dE l z =  r d l      cos 4 1 0 =  Er d  dE  Ez d  z  dz  R P(r,,z)

L长线段在P点产生的电场为：8:dE.dEPPIsin Ode(cosO, -cos,E.dE4元4元60P(r,Φ,z)RPiPZcos Odo =-(sin , - sin )E.L4元r4元若导线无限长,则=0，0,=元PiE.故2元grOE=0Ea2元0E,=0练习2-32025/6/1115

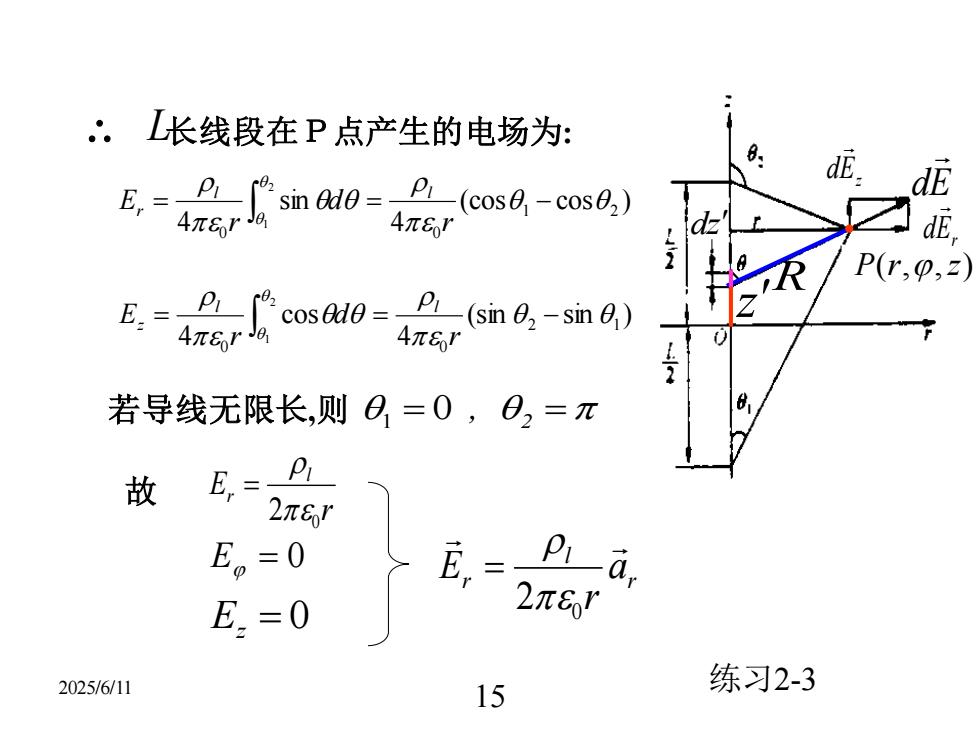
2025/6/11 15 (cos cos ) 4 sin 4 1 2 0 0 2 1             = = −  r d r E l l r 1 = 0 , 2 = (sin sin ) 4 cos 4 2 1 0 0 2 1             = = −  r d r E l l z 若导线无限长,则 故 r E l r 0 2   = = 0 E E z = 0 r l r a r E   0 2   = ∴ L 长线段在Ｐ点产生的电场为: Er d  dE  Ez d  z  dz  R P(r,,z) 练习2-3