
例2-5:已知半径为a的球内、外电场分布为a28元求电荷密度。解:应用高斯定理的微分形式P=V.D=&V.E利用球坐标系中的散度公式162025/6/11
2025/6/11 16 已知半径为 a 的球内、外电场分布为 = a r a a a r a r a a E r r ) , 2 ( ( ) , 2 0 2 0 > < 求电荷密度。 解:应用高斯定理的微分形式 D E = = 0 利用球坐标系中的散度公式 例2-5:

aE1: V.Er sin 0rsin 0 pd1a.p=&r <aroP=V.E)=0r>a8draa28)aar<ri72025/6/11L80
2025/6/11 17 + + = E r E r r E r r E r sin1 (sin ) sin1 ( ) 1 2 2 r a r a r E r r E r 0 2 0 0 2 ( ) 1 = = = r E r a r r E ( r ) 0 1 2 0 0 2 = = = < > = a r a a a r a r a a E r r ) , 2 ( ( ) , 2 0 2 0 > <
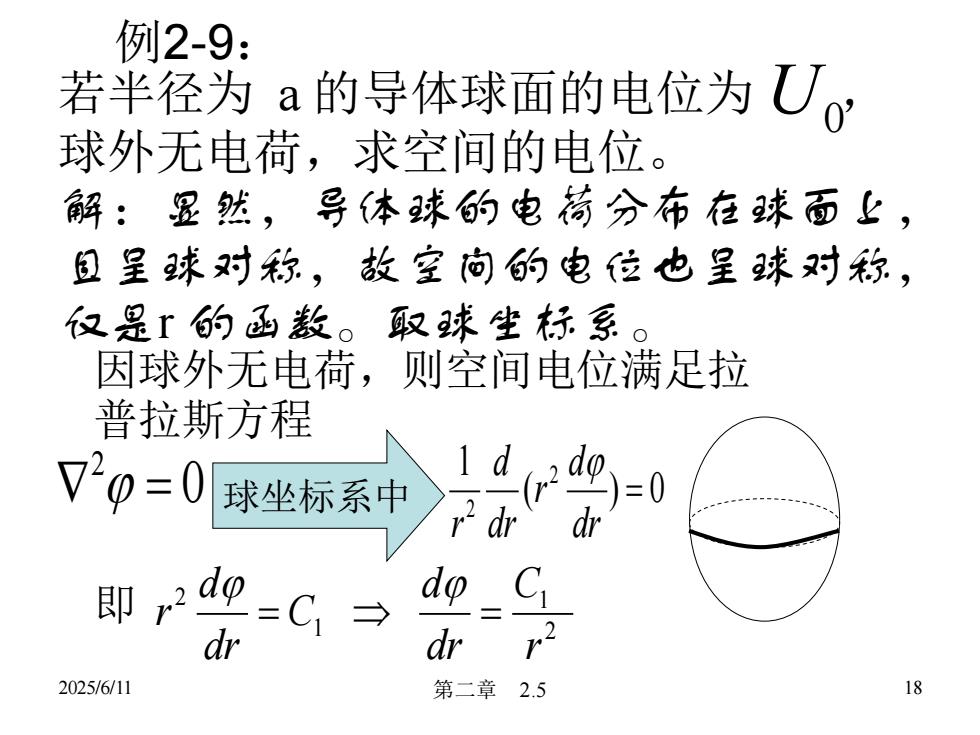
例2-9:若半径为 a的导体球面的电位为U球外无电荷,求空间的电位。解:显然,导体球的电荷分布在球面上,且呈球对称,故室间的电位也呈球对称,仅是r的函数。 取球生标系。因球外无电荷,则空间电位满足拉普拉斯方程=0球坐标系中dldpC即印Cdrdr182025/6/11第二章2.5
2025/6/11 第二章 2.5 18 若半径为 a 的导体球面的电位为 , 球外无电荷,求空间的电位。 U0 解:显然,导体球的电荷分布在球面上, 且呈球对称,故空间的电位也呈球对称, 仅是r 的函数。取球坐标系。 因球外无电荷,则空间电位满足拉 普拉斯方程 0 2 = 球坐标系中 ( ) 0 1 2 2 = dr d r dr d r 即 2 1 1 2 r C dr d C dr d r = = 例2-9:
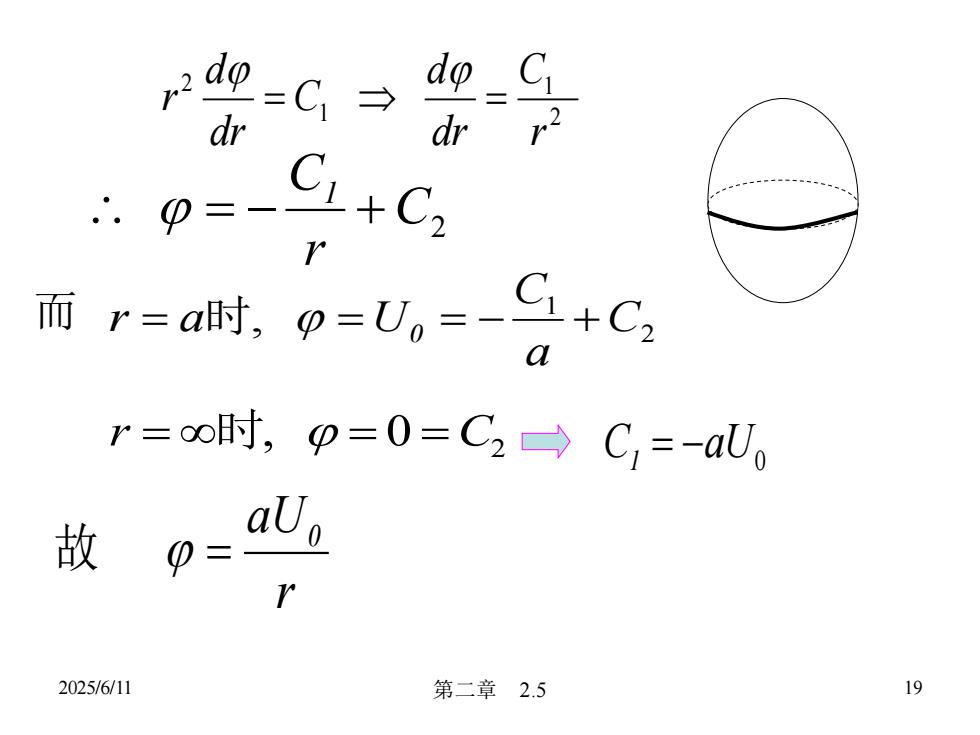
CdpdoC=2drdrC+CDr而 r=a时,=U。=-+C,ar=oo时,β=0=C2C,=-aUaU.故=192025/6/11第二章2.5
2025/6/11 第二章 2.5 19 C2 r C 1 = − + 2 1 1 2 r C dr d C dr d r = = 2 1 , C a C r = a时 =U0 = − + 0 2 r = 时, = =C 而 0 C1 = −aU r aU 0 故 =

例2-6:真空中有电荷以体密度p均匀分布于一半径为R的球中,如图.求球内、球外的电场强度及电位解:R口求电场强度:C(R,0,P)取球心为球生标系的原点。应用高斯通量定理求解较为方便。fE.ds-Zg球内r<RS面取半径为r的球面。60S因电荷分布为球对称,故E的方向为 aR 方向,且仅为r的函数。fe-ds=axE(r)-ax4m2-Zg)1 4rrp6360S
例2-6:真空中有电荷以体密度 均匀分布于一半径 为R的球中,如图.求球内.球外的电场强度及电位. 解: o R ❑ 求电场强度: 应用高斯通量定理求解较为方便。 0 = q E dS S S面取半径为 r 的球面。 因电荷分布为球对称,故 的方向为 方向,且 仅为 r 的函数。 aR E 取球心为球坐标系的原点。 (R,,) 3 0 0 2 1 1 3 1 4 ( ) 4 r q E dS a E r a r R R S = = = 球内 r < R