《电磁场与电磁能》课程PPT教学课件（马冰然版）复习题题

例1-6:： R= 1(x-x')2 +(y-y)? +(z - z)?试证明O其中R=r-r'ZM(x, y,2)M(x,y',z)矢径场点源点!rVx

例1-6： ( ) ( ) ( ) , 2 2 2 R = x − x  + y − y  + z − z  试证明 ) 1 ) ( 1 ( R R  = − z a y a x ax y z    +    +     = 其中    y x o z M (x, y,z) M (x  , y  ,z ) r   r  R = r − r     矢径 源点 场点

V[(x-x)2 +(-y) +(z-z)3j 2证：[(x-x)? +(-y)2 +(z-z)]2P[(x-x) +(-y)2 +(z-z)]2+a[(x-x')2 +(-)2 +(z-z)]2+a静电场5a,(x-x)+a,(y-y)+a.(z-z)[(x-x)2 +(y-y')2 +(z-z)?jRr-rR3<Rr-r

证： 2 1 2 2 2 ) [( ) ( ) ( ) ] 1 ( −  =  x − x  + y − y  + z − z  R 2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −    = x x y y z z x ax  2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −    + x x y y z z y ay  2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −    + x x y y z z z az  2 3 2 2 2 [( ) ( ) ( ) ] ( ) ( ) ( ) x x y y z z a x x a y y a z z x y z −  + −  + −  −  + −  + −  = −    3 3 ) 1 ( r r r r R R R −  −    = − = −      静电场5

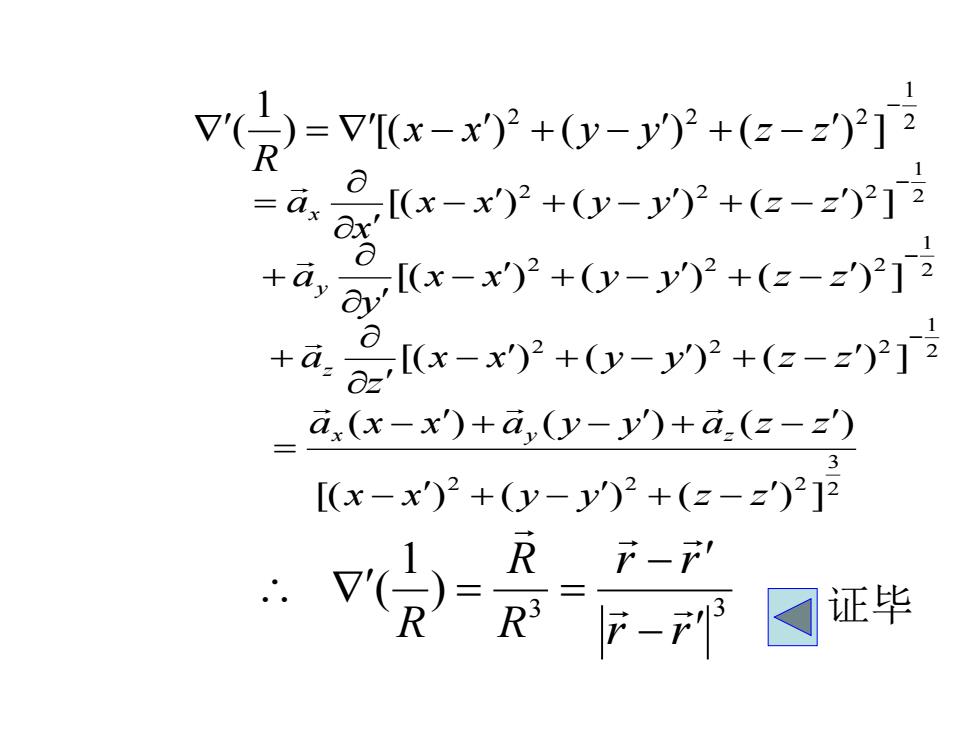
= V[(x-x)? +(y-y')2 +(z-z)j 2R0[(x-x)? +(-y)2 +(z-z)2]2ago[(x-x)? +(-y')2 +(z-z)]2-aX.0[(x-x')2 +(y-y)2 +(z-z)2j2+aaa,(x-x)+a,(y-y)+a,(z-z)[(x-x)? +(y-y')2 +(z-z)j2R-r证毕R3R-

2 1 2 2 2 ) [( ) ( ) ( ) ] 1 ( −  =  x − x  + y − y  + z − z  R 2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −     = x x y y z z x ax  2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −     + x x y y z z y ay  2 1 2 2 2 [( ) ( ) ( ) ] − −  + −  + −     + x x y y z z z az  2 3 2 2 2 [( ) ( ) ( ) ] ( ) ( ) ( ) x x y y z z a x x a y y a z z x y z −  + −  + −  −  + −  + −  =    3 3 ) 1 ( r r r r R R R −  −    = =      证毕

例1-10:沿着在xo面上的一个闭合路径0@求A=ax?+ay?+a2的线积分。此闭合路径由在（0，0）和（2,V2）之间的一段抛物线y2=两段平行于坐标轴的直线段组成，如图yD所示。②计算A的旋度。解：@A.di=(a,x?+a,y+a.2).(a,dx+a,dy+a.d2)=(a,x? +a,y? +a.z).(adx+a,dy)44= xdx+ y2dyfAdi -f'A.di +f'A.di + ,A.di-(x'dx+ydy)+ (x'dx+yd)+ (x'dx+y'dy)

y 例1-10： ①求 2 2 2 A a x a y a z x y z     = + + 沿着在 面上的一个闭合路径C 的线积分。此闭合路径由在（0，0）和（2， 2 ）之间的一 段抛物线 y = x 2 和两段平行于坐标轴的直线段组成，如图 所示。②计算 A 的旋度。  xoy 解：① ( ) ( ) 2 2 2 A dl a x a y a z a dx a dy a dz x y z x y z          = + +  + + x dx y dy a x a y a z a dx a dy x y z x y 2 2 2 2 2 ( ) ( ) = + = + +  +           =  +  +  O D D B B O C A dl A dl A dl A dl            = + + + + + O D D B B O (x dx y dy) (x dx y dy) (x dx y dy) 2 2 2 2 2 2

在路径O>B上，有 y=0,dy=0,x由0→2;在路径 B→>D上，有 x=2,dx=0,y由0→2:在路径 D→0上，有 x由2→0,y由V2→0;:. $ A.di = [(x’dx+ y'dy)+ [' (x’dx+ y'dy)+ [(x?dx+ y'dy)y?dydy0A的环量等于零

y 在路径 O→B 上，有 y = 0,dy = 0; x由0→2; 在路径 B → D 上，有 x = 2,dx = 0, y由0 → 2; 在路径 D →O 上，有 x由2 → 0, y由 2 → 0;       = + + + + + O D D B B O C A dl (x dx y dy) (x dx y dy) (x dx y dy) 2 2 2 2 2 2       = + + + 0 2 2 0 2 2 2 0 2 2 0 2 x dx y dy x dx y dy 0 3 3 3 3 3 3 3 3 0 2 0 2 2 0 2 0 = + + + = x y x y A 的环量等于零。 