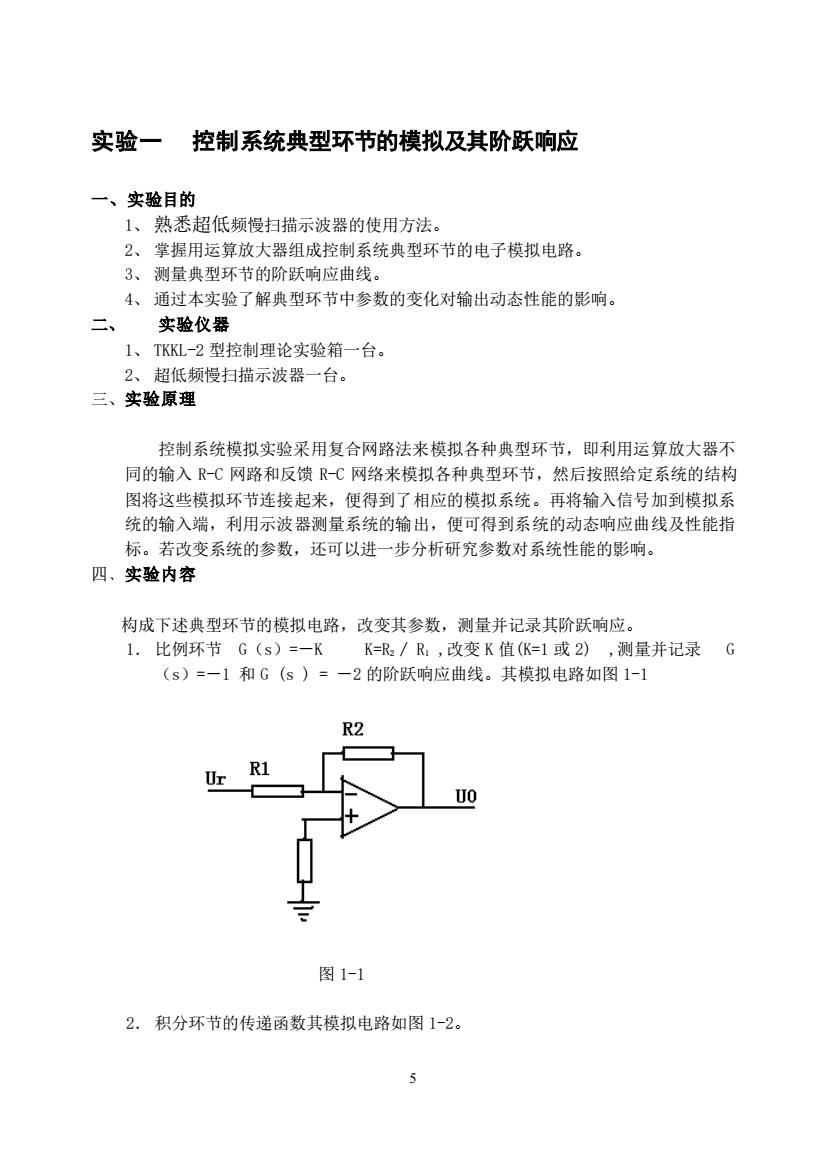
实验一控制系统典型环节的模拟及其阶跃响应一、实验目的1、熟悉超低频慢扫描示波器的使用方法。2、掌握用运算放大器组成控制系统典型环节的电子模拟电路。3、测量典型环节的阶跃响应曲线。4、通过本实验了解典型环节中参数的变化对输出动态性能的影响。二、实验仪器1、TKKL-2型控制理论实验箱一台。2、超低频慢扫描示波器一台。三、实验原理控制系统模拟实验采用复合网路法来模拟各种典型环节,即利用运算放大器不同的输入R-C网路和反馈R-C网络来模拟各种典型环节,然后按照给定系统的结构图将这些模拟环节连接起来,便得到了相应的模拟系统。再将输入信号加到模拟系统的输入端,利用示波器测量系统的输出,便可得到系统的动态响应曲线及性能指标。若改变系统的参数,还可以进一步分析研究参数对系统性能的影响。四、实验内容构成下述典型环节的模拟电路,改变其参数,测量并记录其阶跃响应。1比例环节G(s)=一KK=Rz/Rl,改变K值(K=1或2),测量并记录G(s)=一1和G(s)=一2的阶跃响应曲线。其模拟电路如图1-1R2R1UrUO-图 1-12.积分环节的传递函数其模拟电路如图1-2。5
5 实验一 控制系统典型环节的模拟及其阶跃响应 一、实验目的 1、 熟悉超低频慢扫描示波器的使用方法。 2、 掌握用运算放大器组成控制系统典型环节的电子模拟电路。 3、 测量典型环节的阶跃响应曲线。 4、 通过本实验了解典型环节中参数的变化对输出动态性能的影响。 二、 实验仪器 1、 TKKL-2 型控制理论实验箱一台。 2、 超低频慢扫描示波器一台。 三、实验原理 控制系统模拟实验采用复合网路法来模拟各种典型环节,即利用运算放大器不 同的输入 R-C 网路和反馈 R-C 网络来模拟各种典型环节,然后按照给定系统的结构 图将这些模拟环节连接起来,便得到了相应的模拟系统。再将输入信号加到模拟系 统的输入端,利用示波器测量系统的输出,便可得到系统的动态响应曲线及性能指 标。若改变系统的参数,还可以进一步分析研究参数对系统性能的影响。 四﹑实验内容 构成下述典型环节的模拟电路,改变其参数,测量并记录其阶跃响应。 1. 比例环节 G(s)=-K K=R2 / R1 ,改变 K 值(K=1 或 2) ,测量并记录 G (s)=-1 和 G (s ) = -2 的阶跃响应曲线。其模拟电路如图 1-1 图 1-1 2. 积分环节的传递函数其模拟电路如图 1-2
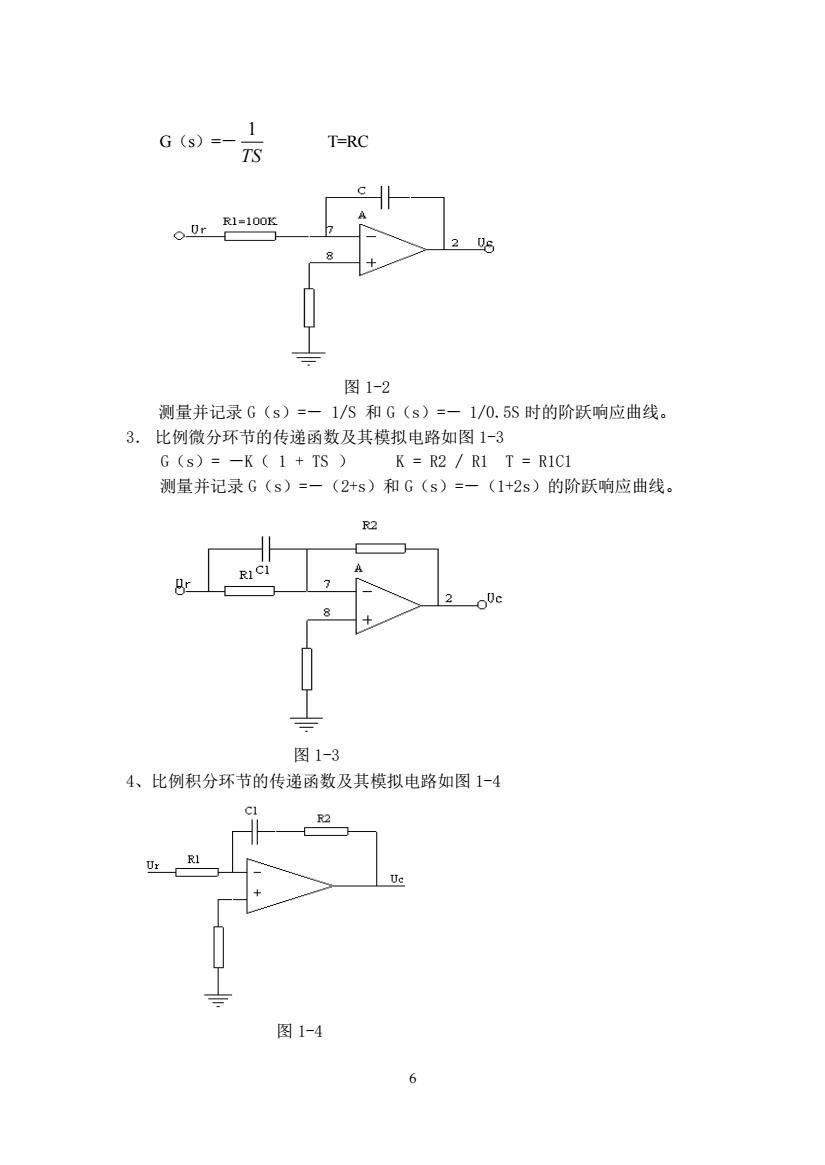
1G (s) =T=RCTSR1=100KQ.0r2068图 1-2测量并记录G(s)=一1/S和G(s)=一1/0.5S时的阶跃响应曲线。比例微分环节的传递函数及其模拟电路如图1-33.G(s)=K(1+TS)K = R2 / R1T = R1C1测量并记录G(s)=一(2+s)和G(s)=一(1+2s)的阶跃响应曲线。R2RICIBrJo-图1-34、比例积分环节的传递函数及其模拟电路如图1-4C1R2R1UrUe图 1-46
6 G(s)=- 1 TS T=RC 图 1-2 测量并记录 G(s)=- 1/S 和 G(s)=- 1/0.5S 时的阶跃响应曲线。 3. 比例微分环节的传递函数及其模拟电路如图 1-3 G(s)= -K( 1 + TS ) K = R2 / R1 T = R1C1 测量并记录 G(s)=-(2+s)和 G(s)=-(1+2s)的阶跃响应曲线。 图 1-3 4、比例积分环节的传递函数及其模拟电路如图 1-4 图 1-4
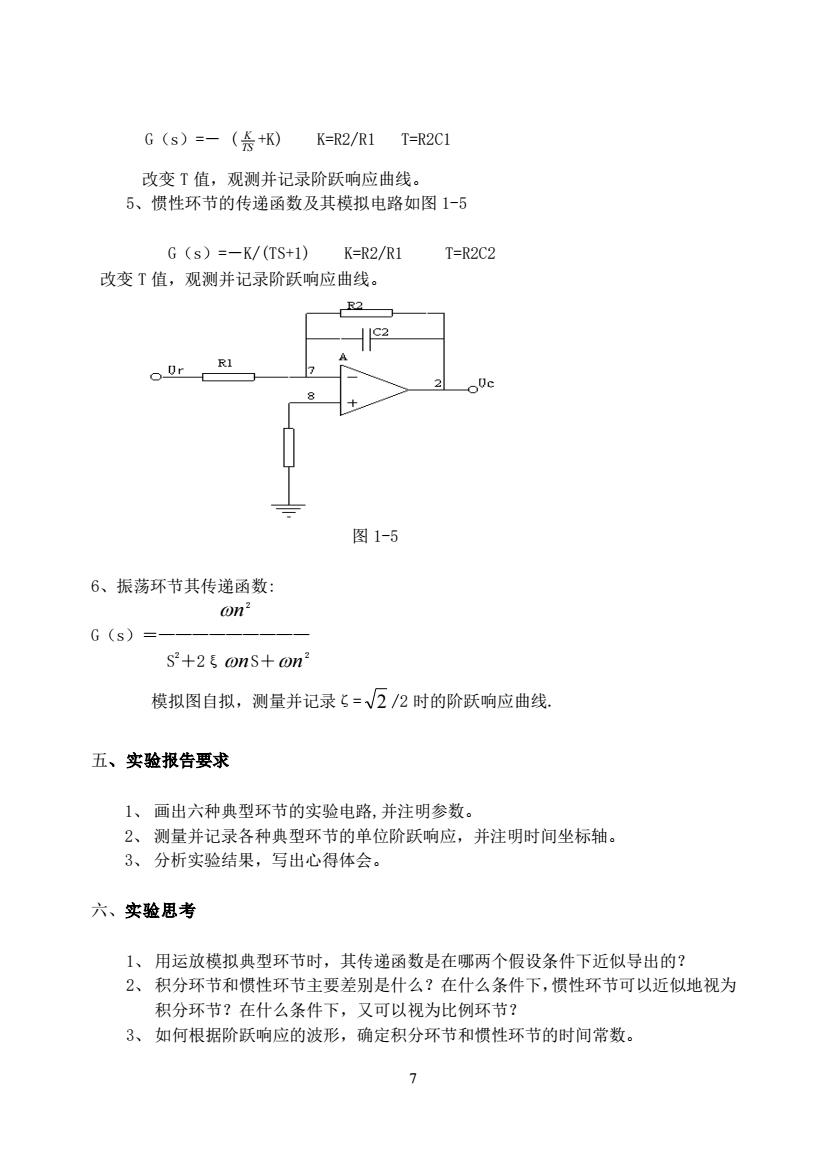
G (s) =-(会+K)K=R2/R1T=R2C1改变T值,观测并记录阶跃响应曲线。5、惯性环节的传递函数及其模拟电路如图1-5K=R2/R1T=R2C2G (s) =-K/(TS+1)改变T值,观测并记录阶跃响应曲线。R2C24R1O_0r0c8图 1-56、振荡环节其传递函数:on?G (s) =s+2onS+on模拟图自拟,测量并记录=2/2时的阶跃响应曲线,五、实验报告要求1、画出六种典型环节的实验电路,并注明参数。2、测量并记录各种典型环节的单位阶跃响应,并注明时间坐标轴。3、分析实验结果,写出心得体会。六、实验思考1、用运放模拟典型环节时,其传递函数是在哪两个假设条件下近似导出的?2、积分环节和惯性环节主要差别是什么?在什么条件下,惯性环节可以近似地视为积分环节?在什么条件下,又可以视为比例环节?3、如何根据阶跃响应的波形,确定积分环节和惯性环节的时间常数。7
7 G(s)=- ( K TS +K) K=R2/R1 T=R2C1 改变 T 值,观测并记录阶跃响应曲线。 5、惯性环节的传递函数及其模拟电路如图 1-5 G(s)=-K/(TS+1) K=R2/R1 T=R2C2 改变 T 值,观测并记录阶跃响应曲线。 图 1-5 6、振荡环节其传递函数: n 2 G(s)=————————— S 2+2ξ n S+ n 2 模拟图自拟,测量并记录ζ= 2 /2 时的阶跃响应曲线. 五、实验报告要求 1、 画出六种典型环节的实验电路,并注明参数。 2、 测量并记录各种典型环节的单位阶跃响应,并注明时间坐标轴。 3、 分析实验结果,写出心得体会。 六、实验思考 1、 用运放模拟典型环节时,其传递函数是在哪两个假设条件下近似导出的? 2、 积分环节和惯性环节主要差别是什么?在什么条件下,惯性环节可以近似地视为 积分环节?在什么条件下,又可以视为比例环节? 3、 如何根据阶跃响应的波形,确定积分环节和惯性环节的时间常数

实验二一阶系统的时域响应及参数测定实验目的1、观测一阶系统在阶跃和斜坡输入信号作用下的瞬态响应。2、根据一阶系统的阶跃响应曲线确定一阶系统的时间常数。二、实验仪器1、TKKL-2型控制理论实验箱一台。2、双踪低频慢扫描示波器一台。三、实验原理1c(s)图2-1为一阶系统的方框图。它的闭环传递函数为TS+1R(s)111: C(t) =l-e-/T令r(t)=1,即R(S)=1/S,!则其输出为C(S)S+1/T/SS(TS +1)C (S)R (S)1TS图 2-1它的阶跃响应曲线如图2-2所示。当t=T时,C(T)=1-e=0.632.这表示当C(t)上升到稳定值的63.2%时,对应的时间就是一阶系统的时间常数T,根据这个原1理,由图2-2可测得一阶系统的时间常数T。当r(t)=t,即R(s)=,系统的输出为1TTC (S) =S(TS+I)S+1/T即C(t)= t-T(1-e/);由于系统的误差e(t)=r(t)-c(t)=T(1-e"/),所以当t→o时,e()=essT,这表明一阶系统能跟踪斜坡信号输入,但有稳态误差存在。其误差的大小为系统的时间常数T8
8 实验二 一阶系统的时域响应及参数测定 一、 实验目的 1、 观测一阶系统在阶跃和斜坡输入信号作用下的瞬态响应。 2、 根据一阶系统的阶跃响应曲线确定一阶系统的时间常数。 二、实验仪器 1、 TKKL-2 型控制理论实验箱一台。 2、 双踪低频慢扫描示波器一台。 三、实验原理 图 2-1 为一阶系统的方框图。它的闭环传递函数为 ( ) ( ) c s R s = 1 TS +1 令 r(t)=1, 即 R(S)=1/S, 则其输出为 C(S)= 1 S TS ( 1) + = 1 S - 1 S T +1/ ;C(t)=1-e -t/T R(S) C(S) _ 图 2-1 它的阶跃响应曲线如图 2-2 所示。当 t=T 时,C(T)=1-e -1 =0.632.这表示当 C(t)上升到稳定值的 63.2﹪时,对应的时间就是一阶系统的时间常数 T,根据这个原 理,由图 2-2 可测得一阶系统的时间常数 T。当 r(t)=t,即 R(s)= 2 1 S ,系统的输出为 C(S)= ( 1) 1 2 S TS + = 2 1 S - S T + S T T +1/ , 即 C(t)= t-T(1-e -t/T); 由于系统的误差 e(t)=r(t)-c(t)=T(1-e -t/T),所以当 t→∞时,e(∞)=ess ==T ,这表明 一阶系统能跟踪斜坡信号输入,但有稳态误差存在。其误差的大小为系统的时间常数 T 。 1 T S

c63. 2%t图2-2四、验内容1、根据图2-1所示的系统,设计相应的模拟实验电路图。2、当r(t)=1v时,观察并记录一阶系统的时间常数T为1S和0.1S时的瞬态响应曲线,并标注时间坐标轴。3、当r(t)=t时,观察并记录一阶系统时间常数T为1S或0.1S的响应曲线。五、实验报告要求1、根据实验,画出一阶系统的时间常数T=1S时的单位阶跃响应曲线,并由实测的曲线求得时间常数T。2、观察并记录一阶系统的斜坡响应曲线,并由图确定跟踪误差e,这一误差值由终值定理求得的值是否相等?分析误差产生的原因。六、实验思考题1、一阶系统为什么对阶跃输入的稳态误差为零,而对单位斜坡输入的稳态误差为T。2、一阶系统的单位斜坡响应能否由其单位阶跃响应求得?试说明之。9
9 C 1 63.2% t 图 2-2 四、验内容 1、 根据图 2-1 所示的系统,设计相应的模拟实验电路图。 2、 当 r(t)=1v 时,观察并记录一阶系统的时间常数 T 为 1S 和 0.1S 时的瞬态响应曲 线,并标注时间坐标轴。 3、 当 r(t)=t 时,观察并记录一阶系统时间常数 T 为 1S 或 0.1S 的响应曲线。 五、实验报告要求 1、 根据实验,画出一阶系统的时间常数 T=1S 时的单位阶跃响应曲线,并由实测的 曲线求得时间常数 T。 2、 观察并记录一阶系统的斜坡响应曲线,并由图确定跟踪误差 ess,这一误差值由 终值定理求得的值是否相等?分析误差产生的原因。 六、 实验思考题 1、 一阶系统为什么对阶跃输入的稳态误差为零,而对单位斜坡输入的稳态误差为 T 。 2、 一阶系统的单位斜坡响应能否由其单位阶跃响应求得?试说明之