2.4控制系统的方块图、信号流图与梅逊公式控制系统的方块图是系统各元件特性、系统结构和信号流向的图解表示法。2.4.1方块图元素(1)方块(BlockDiagram):表示输入到输出单向传输间的函数关系。r(t)c(t)g(s)R(s)+ c(s)4方块信号线图2-14方块图中的方块信号线:带有箭头的直线,箭头表示信号的流向,在直线旁标记信号的时间函数或象函数。(2)比较点(合成点、综合点)SummingPoint两个或两个以上的输入信号进行加减比较的元件,“+”表示相加,“”表示相减。“+”号可省略不写。T1T 1+T 2R(s)-R(s)R(s)++R(s)T 2T3T1T1-T2+T3T 2图2-15比较点示意图注意:进行相加减的量,必须具有相同的量刚。(3)分支点(引出点、测量点)BranchPoint表示信号测量或引出的位置32
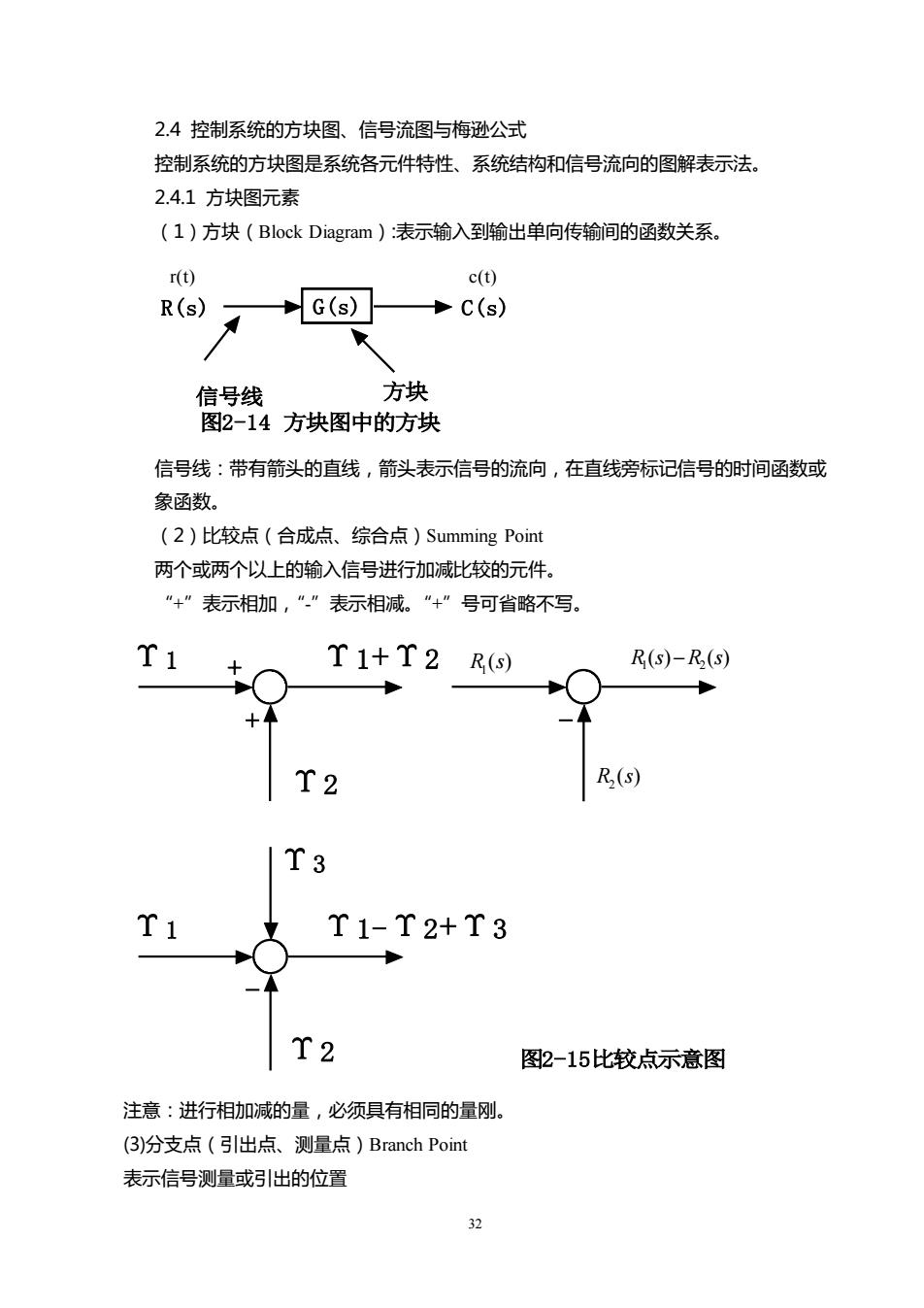
32 2.4 控制系统的方块图、信号流图与梅逊公式 控制系统的方块图是系统各元件特性、系统结构和信号流向的图解表示法。 2.4.1 方块图元素 (1)方块(Block Diagram):表示输入到输出单向传输间的函数关系。 R(s) G(s) C(s) 图2-14 方块图中的方块 信号线 方块 r(t) c(t) 信号线:带有箭头的直线,箭头表示信号的流向,在直线旁标记信号的时间函数或 象函数。 (2)比较点(合成点、综合点)Summing Point 两个或两个以上的输入信号进行加减比较的元件。 “+”表示相加,“-”表示相减。“+”号可省略不写。 Υ + 1 Υ1+Υ2 Υ2 + - ( ) ( ) 1 2 R s −R s ( ) 1 R s ( ) 2 R s Υ1 Υ1-Υ2+Υ3 Υ2 - Υ3 图2-15比较点示意图 注意:进行相加减的量,必须具有相同的量刚。 (3)分支点(引出点、测量点)Branch Point 表示信号测量或引出的位置
c(s)R(s)P(s)G(s)G,(s)P(s)图2-16分支点示意图注意:同一位置引出的信号大小和性质完全一样。2.4.2几个基本概念及术语N(s)E(s)++R(s)G,(s)G;(s)B(s)H(s)打开反馈图2-17反馈控制系统方块图(1)前向通路传递函数假设N(s)=0打开反馈后,输出C(s)与R(s)之比。在图中等价于C(s)与误差E(s)之比C() = G(s)G,(s)=G(s)E(s)(2)反馈回路传递函数FeedforwardTransferFunction假设N(s)=0主反馈信号B(s)与输出信号C(s)之比B(s) = H(s)C(s)(3)开环传递函数Open-loopTransferFunction假设N(s)=0主反馈信号B(s)与误差信号E(s)之比。33
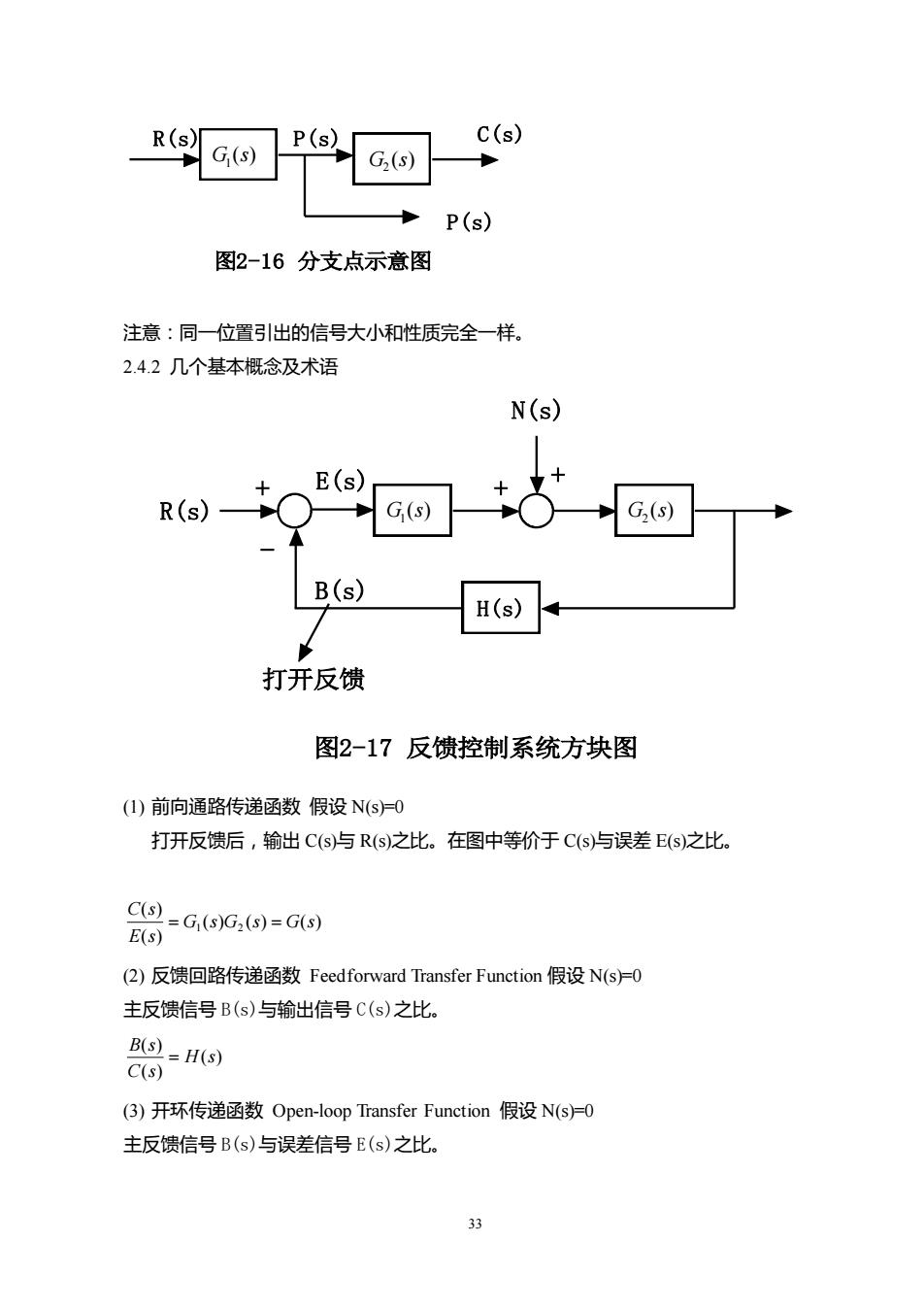
33 图2-16 分支点示意图 P(s) R(s) P(s) C(s) ( ) 1 G s ( ) 2 G s 注意:同一位置引出的信号大小和性质完全一样。 2.4.2 几个基本概念及术语 + + H(s) - + R(s) E(s) B(s) N(s) 打开反馈 ( ) 1 G s ( ) 2 G s 图2-17 反馈控制系统方块图 (1) 前向通路传递函数 假设 N(s)=0 打开反馈后,输出 C(s)与 R(s)之比。在图中等价于 C(s)与误差 E(s)之比。 ( ) ( ) ( ) ( ) ( ) 1 2 G s G s G s E s C s = = (2) 反馈回路传递函数 Feedforward Transfer Function 假设 N(s)=0 主反馈信号 B(s)与输出信号 C(s)之比。 ( ) ( ) ( ) H s C s B s = (3) 开环传递函数 Open-loop Transfer Function 假设 N(s)=0 主反馈信号 B(s)与误差信号 E(s)之比
B(=G(s)G;(s)H(s)=G()H(s)E(s)(4)闭环传递函数Closed-loopTransferFunction假设N(s)=0输出信号 C(s)与输入信号R(s)之比G(s)C(s) _G,(s)G,(s)R(s)1+H(s)G(s)1+ H(s)G(s)推导:因为C(s)=E(s)G(s)=[R(s)-C(s)H(s)G(s)G(s)右边移过来整理得 C(s)R(s)1+ H(s)G(s)G(s)即C(s)前向通路传递函数R(s)1+H(s)G(s)1+开环传递函数(5)误差传递函数假设N(s)=0误差信号E(s)与输入信号R(s)之比。将C(s)=E(s)G(s)代入上式,消去G(s)即得:11E(s)R(s)1+H(s)G(s)1+开环传递函数(6)输出对扰动的传递函数假设R(s)=0N(s)G,(s)C(s)H(s)G.CS图2-18输出对扰动的结构图G,(s)C(s)由图2-18,利用公式**,直接可得:Mx(s)N(s)1+G(s)H(s)(7)误差对扰动的传递函数假设R(s)=0G(s)H(s)N(s)★ E(s)G;(s)图2-19误差对扰动的结构图34
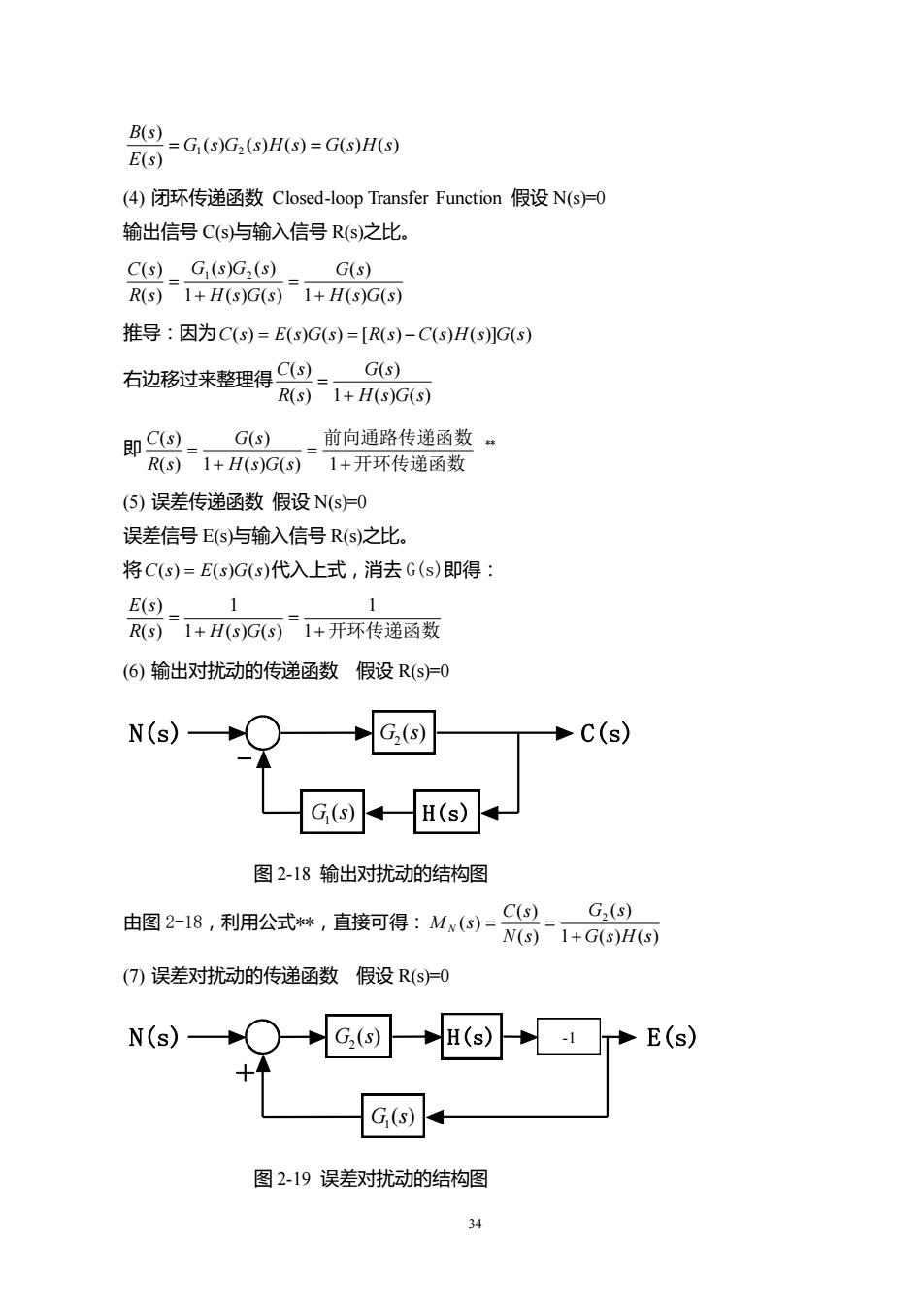
34 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 G s G s H s G s H s E s B s = = (4) 闭环传递函数 Closed-loop Transfer Function 假设 N(s)=0 输出信号 C(s)与输入信号 R(s)之比。 1 ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) 1 2 H s G s G s H s G s G s G s R s C s + = + = 推导:因为 C(s) = E(s)G(s) = [R(s) −C(s)H(s)]G(s) 右边移过来整理得 1 ( ) ( ) ( ) ( ) ( ) H s G s G s R s C s + = 即 开环传递函数 前向通路传递函数 + = + = 1 ( ) ( ) 1 ( ) ( ) ( ) H s G s G s R s C s ** (5) 误差传递函数 假设 N(s)=0 误差信号 E(s)与输入信号 R(s)之比。 将 C(s) = E(s)G(s) 代入上式,消去 G(s)即得: +开环传递函数 = + = 1 1 1 ( ) ( ) 1 ( ) ( ) R s H s G s E s (6) 输出对扰动的传递函数 假设 R(s)=0 - N(s) C(s) H(s) ( ) 2 G s ( ) 1 G s 图 2-18 输出对扰动的结构图 由图 2-18,利用公式**,直接可得: 1 ( ) ( ) ( ) ( ) ( ) ( ) 2 G s H s G s N s C s M s N + = = (7) 误差对扰动的传递函数 假设 R(s)=0 N(s) H(s) E(s) + ( ) 1 G s ( ) 2 G s -1 图 2-19 误差对扰动的结构图

由图2-19,利用公式**,直接可得:E(s) - -G,(s)H(s)M ne (s) =N(s)1+G(s)H(s)线性系统满足叠加原理,当控制输入R(s)与扰动N(s)同时作用于系统时,系统的输出及误差可表示为:G(s)G,(s)N(s)C(s)= 7R(s) +1+G(s)H(s)1+G(s)H(s)1G;(s)H() N(s)E(s) =R(s)-1+G(s)H(s)1+G(s)H(s)注意:由于N(s)极性的随机性,因而在求E(s)时,不能认为利用N(s)产生的误差可抵消R(s)产生的误差。2.4.3方块图的绘制(1)考虑负载效应分别列写系统各元部件的微分方程或传递函数,并将它们用方框(块)表示。(2)根据各元部件的信号流向,用信号线依次将各方块连接起来,便可得到系统的方块图。系统方块图-也是系统数学模型的一种。例2-8画出下列RC电路的方块图ROOu,uo1O(a)图2-20一阶RC网络解:由图2-20,利用基尔霍夫电压定律及电容元件特性可得:u, -u.[(s) - U()-U,(a)(1)RR对其进行拉氏变换得:[idt[U (s)= 1()(2)uosCc由(1)和(2)分别得到图(b)和(c)。35
35 由图 2-19,利用公式**,直接可得: 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 G s H s G s H s N s E s M s NE + − = = 线性系统满足叠加原理,当控制输入 R(s)与扰动 N(s)同时作用于系统时,系统的 输出及误差可表示为: ( ) 1 ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) 2 N s G s H s G s R s G s H s G s C s + + + = ( ) 1 ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) 1 ( ) 2 N s G s H s G s H s R s G s H s E s + − + = 注意:由于 N(s)极性的随机性,因而在求 E(s)时,不能认为利用 N(s)产生的误差可抵 消 R(s)产生的误差。 2.4.3 方块图的绘制 (1)考虑负载效应分别列写系统各元部件的微分方程或传递函数,并将它们用方框(块) 表示。 (2)根据各元部件的信号流向,用信号线依次将各方块连接起来,便可得到系统的方 块图。 系统方块图-也是系统数学模型的一种。 例 2-8 画出下列 RC 电路的方块图。 R C i (a) ui uo 图 2-20 一阶 RC 网络 解:由图 2-20,利用基尔霍夫电压定律及电容元件特性可得: = − = c idt u R u u i o i o 对其进行拉氏变换得: = − = (2) ( ) ( ) (1) ( ) ( ) ( ) sC I s U s R U s U s I s o i o 由(1)和(2)分别得到图(b)和(c)
U,(s)I(s)4C1I (s)U.(s)SCU.(s)(b)(c)将图(b)和(c)组合起来即得到图(d),图(d)为该一阶RC网络的方块图。U.(s)I (s)1U,(s)RSCU.(s)(d)例2-9画出下列R-C网络的方块图。R2R,ii,uC,C.u,O(a)电路图RR2Uc (s)O.中1U.(s)U,(s)sC2sC,I,(s),(s)O(b)运算电路图解:(1)根据电路定理列出方程,写出对应的拉氏变换,也可直接画出该电路的运算电路图如图(b);(2)根据列出的4个式子作出对应的框图;(3)根据信号的流向将各方框依次连接起来。36
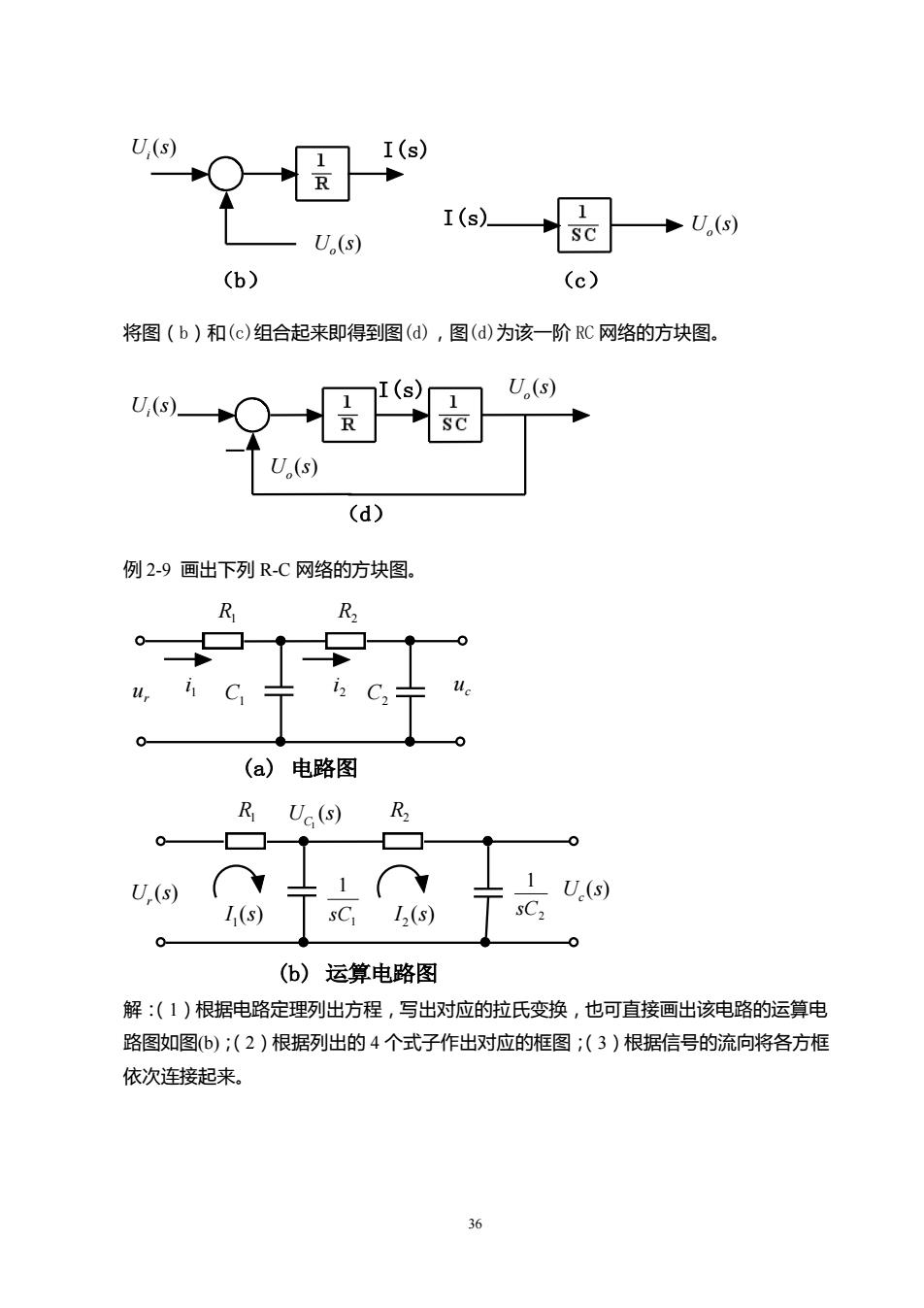
36 (b) Ui (s) I(s) U (s) o I(s) (c) U (s) o 将图(b)和(c)组合起来即得到图(d),图(d)为该一阶 RC 网络的方块图。 - I(s) (d) U (s) o U (s) o U (s) i 例 2-9 画出下列 R-C 网络的方块图。 (a) 电路图 ur 1 i 2 i R1 R2 uc C1 C2 (b) 运算电路图 R1 ( ) R2 1 U s C U (s) r U (s) c ( ) 1 I s ( ) 2 I s 1 1 sC 2 1 sC 解:(1)根据电路定理列出方程,写出对应的拉氏变换,也可直接画出该电路的运算电 路图如图(b);(2)根据列出的 4 个式子作出对应的框图;(3)根据信号的流向将各方框 依次连接起来