
导航、 三、空间四边形 【问题思考】 1.四条边都相等的四边形一定是菱形吗? 提示:不一定
导航 三、空间四边形 【问题思考】 1.四条边都相等的四边形一定是菱形吗? 提示:不一定
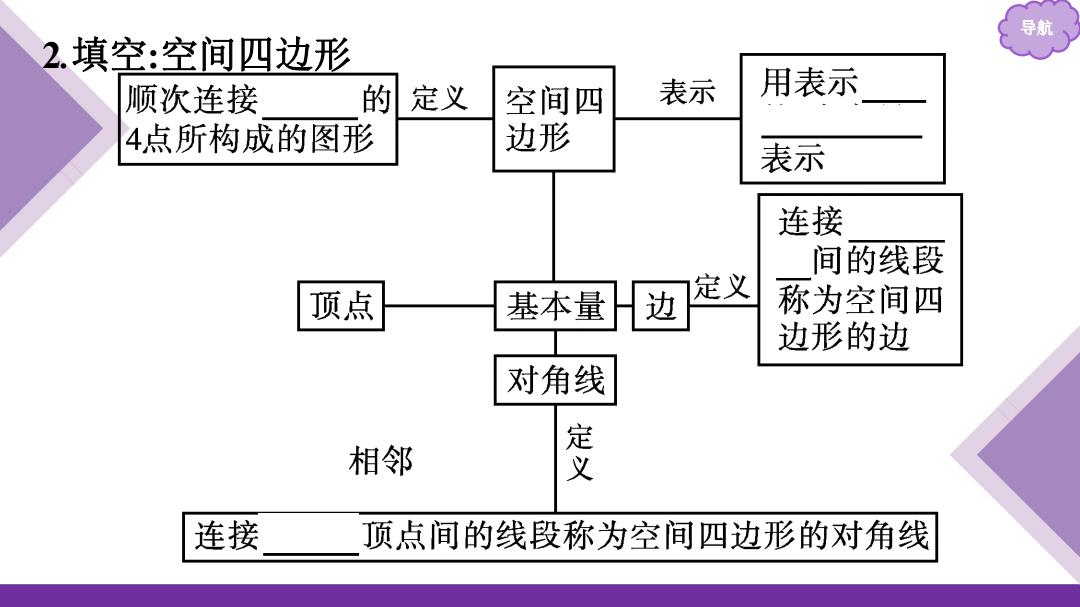
导航 2.填空:空间四边形 顺次连接 的 定义 空间四 表示 用表示 4点所构成的图形 边形 表示 连接 间的线段 顶点 基本量 边 定义 称为空间四 边形的边 对角线 定 相邻 连接 顶点间的线段称为空间四边形的对角线
导航 2.填空:空间四边形

导航 3.做一做:对于空间四边形,下面说法正确的是 (填序 号) ①空间四边形的两条对角线是异面直线; ②存在对边平行的空间四边形; ③若空间四边形的对角互补,则它内接于圆; ④四条线段首尾顺次连接就构成空间四边形 答案:①
导航 3.做一做:对于空间四边形,下面说法正确的是 .(填序 号) ①空间四边形的两条对角线是异面直线; ②存在对边平行的空间四边形; ③若空间四边形的对角互补,则它内接于圆; ④四条线段首尾顺次连接就构成空间四边形. 答案:①

导月 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√”,错误 的画“X” (1)空间四边形的四个顶点一定不共面.(√) (2)过直线外一点且与这条直线异面的直线有无数条.(√) 3)直线a,b与两条异面直线分别对应平行,则a与b异面.(X (4)如果两条直线没有交点,那么这两条直线平行.(×)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√” ,错误 的画“×” . (1)空间四边形的四个顶点一定不共面.( ) (2)过直线外一点且与这条直线异面的直线有无数条.( ) (3)直线a,b与两条异面直线分别对应平行,则a与b异面.( ) (4)如果两条直线没有交点,那么这两条直线平行.( ) √ √ × ×

导月 课堂·重难突破 探究一空间平行线的传递性的应用 【例1】在长方体ABCD-A1B1CD1中, A E,F分别是棱AA1,CC1的中点. E 求证:四边形B,EDF是平行四边形 A B 分析:通过证明B1E∥DF,且B1E=DF来证明四边形B1EDF为 平行四边形
导航 课堂·重难突破 探究一 空间平行线的传递性的应用 【例1】 在长方体ABCD-A1B1C1D1中, E,F分别是棱AA1 ,CC1的中点. 求证:四边形B1EDF是平行四边形. 分析:通过证明B1E∥DF,且B1E=DF来证明四边形B1EDF为 平行四边形