
某些重要平面点集的定义 开集一若平面点集所属的每一个点都是E的内点,则称E 为开集。 闭集一若平面点集E的所有聚点都属于E,则称E为闭集, 若点集没有聚点,这时也称为闭集。 开区域一若非空开集E具有连通性,则称E为开域。 闭区域一开域连同其边界所组成的点集称为闭域。 区域一开区域、闭区域,或者开区域连同其一部分界点 所成的点集,统称为区域
开集—若平面点集所属的每一个点都是 的内点,则称 为开集。 E E 闭集—若平面点集 的所有聚点都属于 ,则称 为闭集, 若点集 没有聚点,这时也称 为闭集。 E E E E E 开区域—若非空开集 E 具有连通性 ,则称 E 为开域。 某些重要平面点集的定义 闭区域—开域连同其边界所组成的点集称为闭域。 区域—开区域、闭区域,或者开区域连同其一部分界点 所成的点集,统称为区域
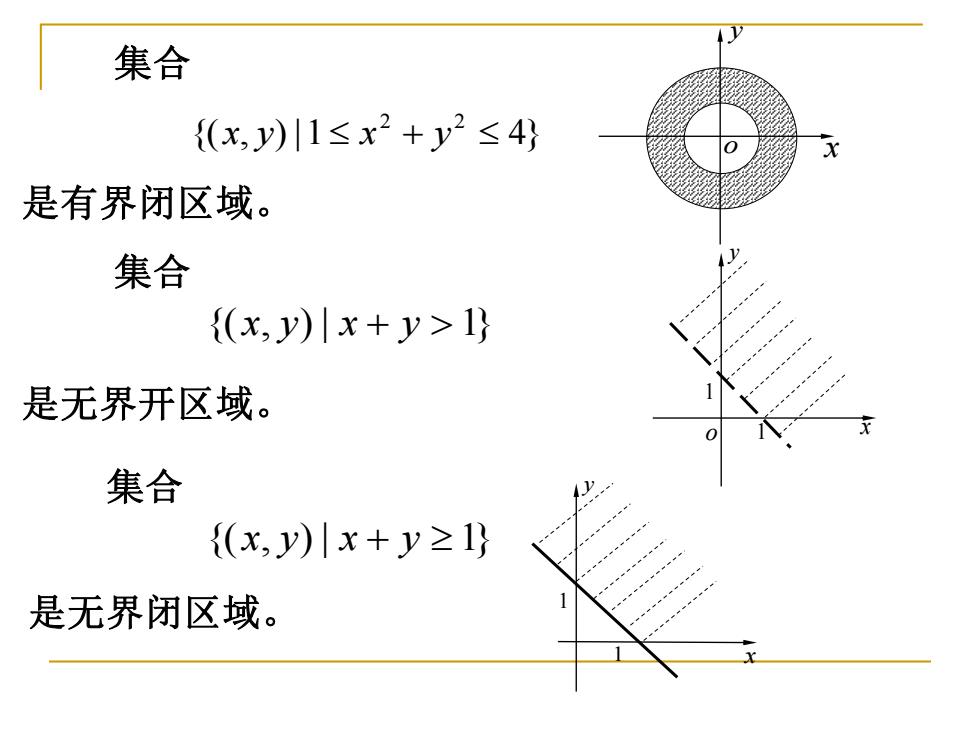
集合 {(x,y)川1≤x2+y2≤4} 是有界闭区域。 集合 出 (x,y)川x+y>1} e-m 是无界开区域。 集合 {(x,y)川x+y≥1 是无界闭区域
{( , ) |1 4} 2 2 x y x + y 是有界闭区域。 集合 {( x, y) | x + y 1} 是无界开区域。 集合 {( x, y) | x + y 1} 是无界闭区域。 集合 y o x y x 1 o 1 y x 1 1

二、多元函数的概念 例4设银行存款利率为r,将10000元存入银行,不 计复利,则t年后的本利和为: M=10000(1+r)' 当和的值取定后,则的对应值也随之确定. 例5圆柱体的侧面积S,底半径和高h之间具有 关系: S=2πrh 当r、h在集合{(r,h)川r>0,h>0;内取定一对值(r,h) 时,S的对应值就随之确定
二、 多元函数的概念 例4 设银行存款利率为r,将10000元存入银行,不 计复利,则t 年后的本利和为: 当r和t的值取定后,则的对应值也随之确定. t M =10000 (1+ r) 例5 圆柱体的侧面积S,底半径r和高h之间具有 关系: 当r、h在集合 内取定一对值 时, S的对应值就随之确定. S = 2 r h {(r,h) | r 0,h 0} (r,h)

例6一定量的理想气体的压强p、体积和绝对 温度T之间具有关系 RT p= 其中R为常数.当V、T在集合(V,T)1V>0,T>To}内取 定一对值(W,T)时,p的对应值就随之确定
例6 一定量的理想气体的压强 p、体积V和绝对 温度T之间具有关系 其中R为常数.当V、T在集合 内取 定一对值 时, 的对应值就随之确定. RT p V = {( , ) | 0, } V T V T T0 (V ,T ) p