北京化工大学：《微积分》课程授课教案（专题讲稿）工科数学分析专题——函数项级数

例 1、证明级数sinx+sim2x+…+sinn产+…在(，切)上一致收敛 1222 n2 明级致空1京（国上资收酸 2、1 3、 证明级数∑ne“在[6，+o∞)上一致收敛，6>0常数

例       2 2 2 2 2 4 2 1 1 sin sin 2 sin 1 , 1 2 2 , 1 3 , 0 n nx n x x n x n x n x ne                     、证明级数  在 上一致收敛 、证明级数 在 上一致收敛 、证明级数 在 上一致收敛, 常数

一 致收敛级数和函数的连续性 设4，(x)在[a,b上连续，若∑4，(x)在[a,b]上一致收敛于S(x,那么和函数 S(x)也在a,b]上连续 证明：S(x)-S(x) S(x)-Sx(x)+Sy (x)-Sy(xo)+Sx (x)-S(xo)

一致收敛级数和函数的连续性 1 ( ) [ , ] , ( ) [ , ] ( ), ( ) [ , ] n n n u x a b u x a b S x S x a b   设 在 上连续 若 在 上一致收敛于 那么和函数 也在 上连续 0 0 0 0 ( ) ( ) ( ) ( ) ( ) ( ( ) ) ( ) N N N N S x S S x S S x S S x S x x x  x       证明：

一致收敛级数和函数的可积性 设，(x)在a,b]上可积，若∑4，(x)在[a,b1上一致收敛于S(x,那么S(x)地 每a止可积且vxea小2a,(h-2a(s 证明：∑4(ew-24(x边 ≤位4-24体≤24-立4w恤 ≤e(b-a

一致收敛级数和函数的可积性   1 1 1 ( ) [ , ] , ( ) [ , ] ( ), ( ) [ , ] , , ( ) ( ) n n n n x n n x a n a u x a b u x a b S x S x a b x a b u x dx u x dx              设 在 上可积 若 在 上一致收敛于 那么 也 在 上可积，且   1 1 1 1 1 1 ( ) ( ) ( ) ( ) ( ) ( ) n x x k k a a k k n n x b k k k k a a k k k k u x dx u x dx u x u x dx u x u x dx  b a                           证明：

一致收敛级数和函数的可导性 设，()eC'0,neN,若∑，(x在I上处处收敛于S(x):I→R,∑，() 在I上一致收敛到o(x):I→R, 则和函数2（国c[含(j-立o 证明2，odi-2uo0dh-立u(e-三u) 从吃ao-20咖-②j 因此（交4ecu.即2u)eC

一致收敛级数和函数的可导性 1 1 1 1 1 1 1 ( ) ( ), ( ) ( ) : , ( ) ( ) : , ( ) ( ), ( ) ( ) n n n n n n n n n n n u x C I n u x I S x I u x I x I u x C I u x u x                                    设 ,若 在 上处处收敛于 在 上一致收敛到 则和函数 且     0 0 0 0 1 1 1 1 1 1 1 1 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) , ( ) x x n n n n x x n n n n x n n n x n n n n n n n u t dt u t dt u x u x d u t u t dt u x dx u x C I u x C I                                                              证明： 从而 因此 即

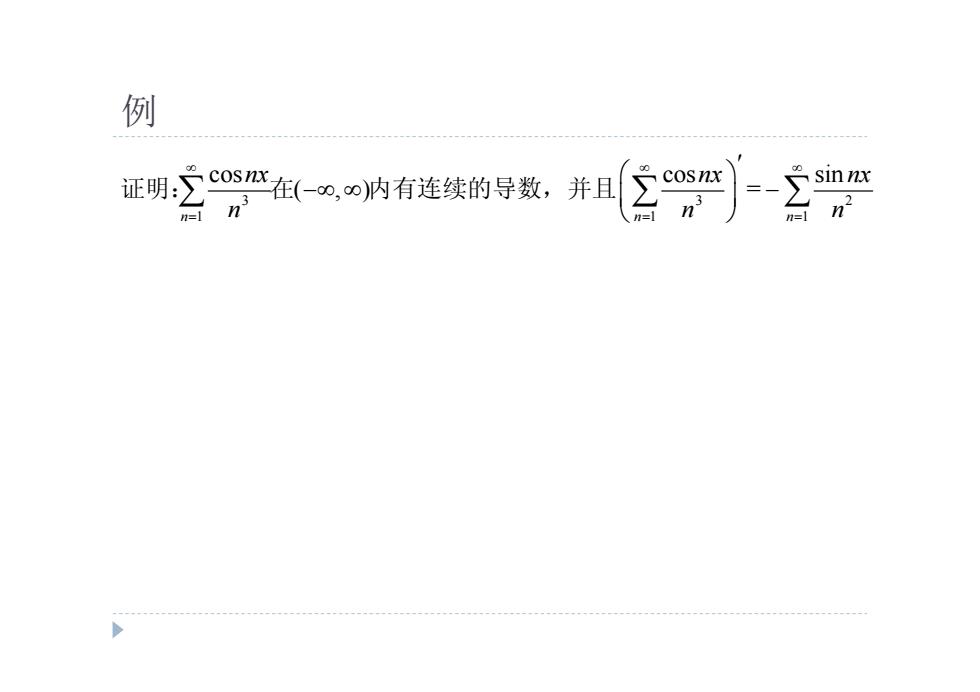
例 正明空严任女网消有连续的子数。并 cosnx n=1 =1 n 2

例 3 3 2 1 1 1 cos cos sin ( , ) = n n n nx nx nx n n n                 证明：   在 内有连续的导数，并且