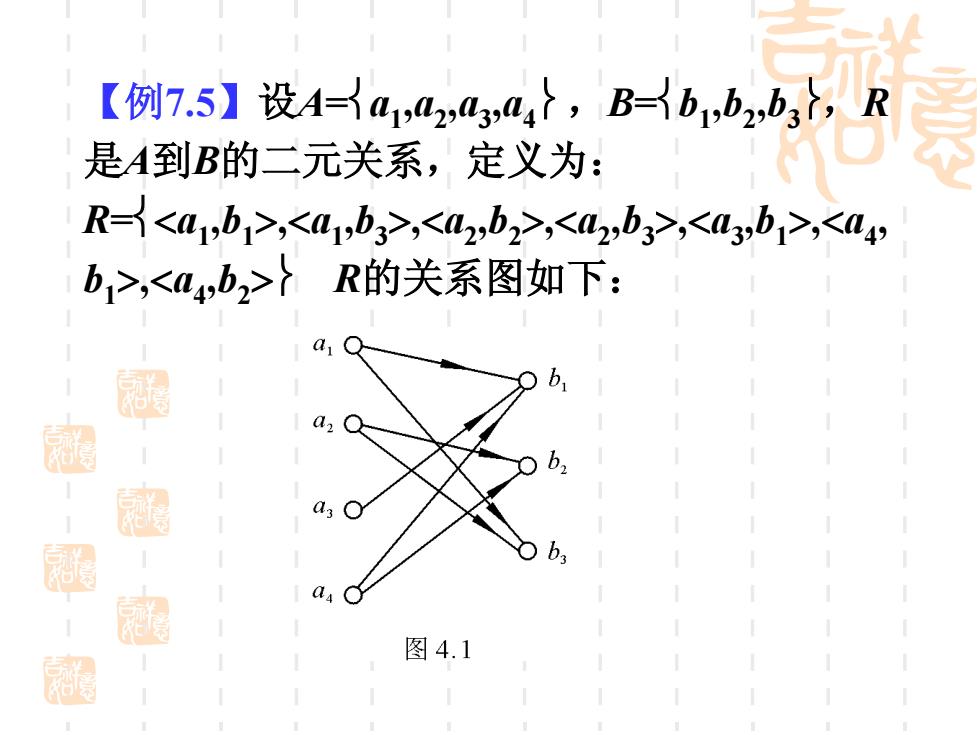
【例7.5】设Aa1,2,43,4},B=b1,b2,b3,R 是A到B的二元关系,定义为: R<a1,b1>,<a1,b3>,<2,b2>,<a2,b3><3,b1>,<4 b1>,<a4,b2>?R的关系图如下: 0 图4.1
【例7.5】设A=a1 ,a2 ,a3 ,a4 ,B=b1 ,b2 ,b3 ,R 是A到B的二元关系,定义为: R=a1 ,b1 ,a1 ,b3 ,a2 ,b2 ,a2 ,b3 ,a3 ,b1 ,a4 , b1 ,a4 ,b2 R的关系图如下:

(2)A上的二元关系R的关系图 设Aa1,2,.,m},R是A上的二元关 系,其关系图如下绘制: ①画出m个小点表示A的元素。 ②如果<a,>∈R,则从a,到a画一根有 制 方向(带箭头)的线。 超
⑵A上的二元关系R的关系图 设A=a1 ,a2 , „ ,am ,R是A上的二元关 系,其关系图如下绘制: ①画出m个小点表示A的元素。 ②如果ai ,aj R,则从ai到aj画一根有 方向(带箭头)的线
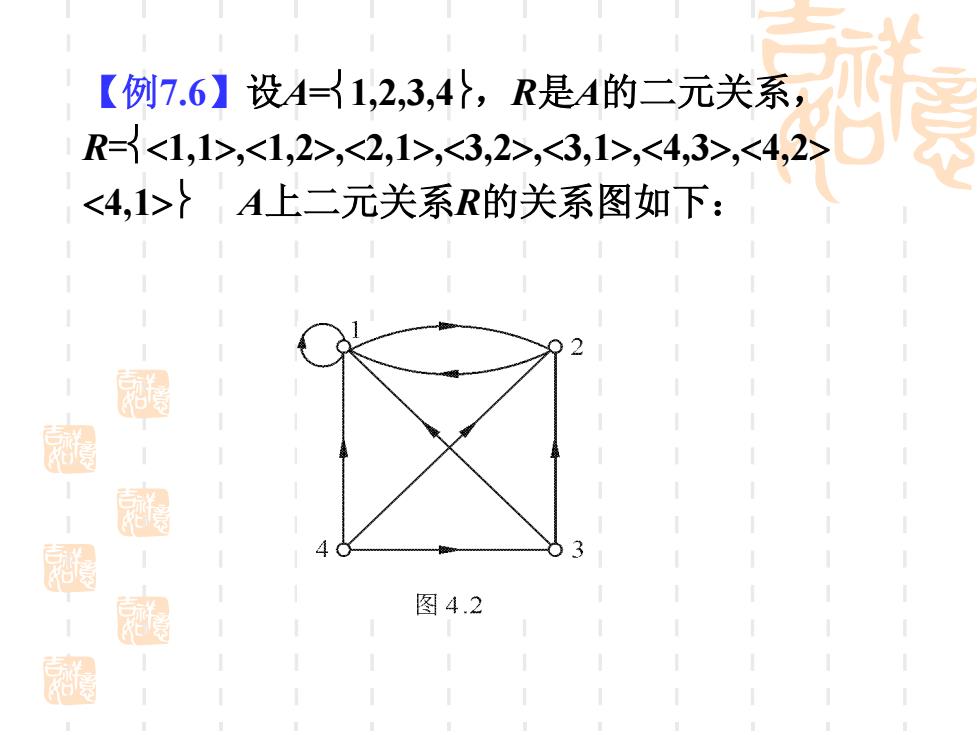
【例7.6】设A=1,2,3,47,R是A的二元关系, R<1,1>,<1,2>,<2,1>,<3,2>,<3,1>,<4,3>,<4,2> <4,1>}A上二元关系R的关系图如下: 图4.2
【例7.6】设A=1,2,3,4,R是A的二元关系, R=1,1,1,2,2,1,3,2,3,1,4,3,4,2 4,1 A上二元关系R的关系图如下:

§73关系的运算 一、 基本运算 定义4.2.1设A,B是集合,RCAXB。 domR=<xy>∈R冫叫做R的定义域。 厨 ran R=yl<x,y>∈R叫做R的值域。 1dR=dom RUran R叫做R的域。 酸
§7.3关系的运算 一、基本运算 定义4.2.1设A,B是集合,RA×B。 dom R=x|x,yR 叫做R的定义域。 ran R=y| x,yR 叫做R的值域。 fld R= dom R∪ran R叫做R的域

逆运算 定义4.2.4设R为二元关系,集合 {y,><x>eR} 叫做R的逆关系。记为Rl 容易证明,R/的关系矩阵MR,是R的 关系矩阵MR的转置矩阵,即MR,=MRT 。可以验证,将R关系图中的弧线的箭头 反置,就可以得到R1关系图
逆运算 定义4.2.4 设R为二元关系,集合 y,xx,yR 叫做R的逆关系。记为R-1 容易证明, R-1 的关系矩阵 MR-1是R的 关系矩阵MR的转置矩阵,即 MR-1 =MR T 可以验证,将R关系图中的弧线的箭头 反置,就可以得到R-1 关系图