复旦大学：《统计热力学》课程教学资源（课件讲稿）07 Monte Carlo方法及其在化学中的应用 §7.2 分子动力学模拟 模拟分子动力学模拟及其在化学中的应用

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Inovative Material 三种算法的比较 a.Verlet;b.Leap flog;c.Velocity Verlet (a)1-6t t 1+t t-Ot t 1+8t t-t t 1+6t t-t t t+δt r a (c) r 10/14/2013 第七章-2MD方法 16造

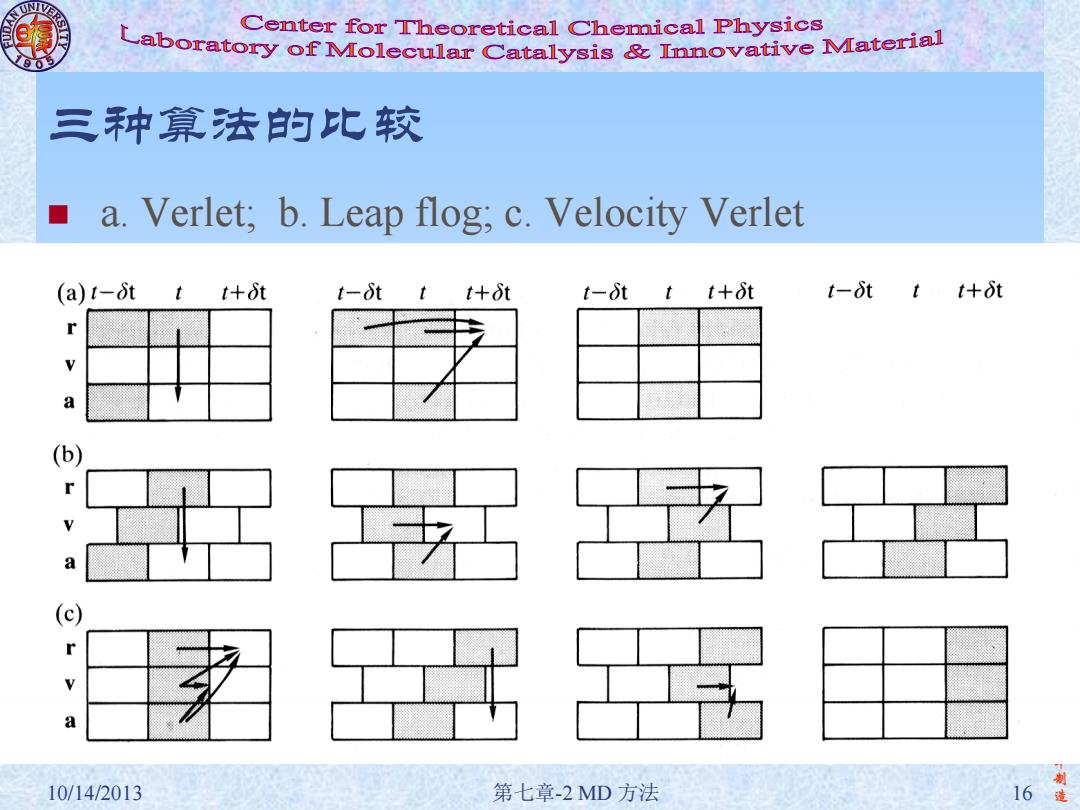
李 振 华 制 10/14/2013 第七章-2 MD 方法 16 造 三种算法的比较  a. Verlet; b. Leap flog; c. Velocity Verlet

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mvative Material 有限差分方法(Finite Difference Methods) ■Verlet算法的改进3 ■Beeman's算法(Beeman,1976) r+-r0+0a+a0ea-成a 6 +=0-写0a-名a40a-石- 李振华 10/14/2013 第七章-2MD方法 17 造

李 振 华 制 10/14/2013 第七章-2 MD 方法 17 造 有限差分方法(Finite Difference Methods)  Verlet算法的改进3  Beeman’s 算法(Beeman, 1976) t t t t t t t t t t t t t t t t t t t t           ( ) 6 1 ( ) 6 5 ( ) 3 1 ( ) ( ) ( ) 6 1 ( ) 3 2 ( ) ( ) ( ) 2 2             v v a a a r r v a a

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material Predictor-Corrector integration methods (Gear,1971) 利用Taylor展开式计算下一时刻的位置，速度，加 速度及其它高级项 ■把实际计算a(t什δ的与预测的a(t什6t)作比轻 Aa(t+ot)=a(t+t)-a(t+t) r(t+8t)=r(t+8t)+coAa(t+8t) v(t+8t)=v(t+8t)+cAa(t+8t) a(t+t)/2=a(t+t)/2+c2Aa(t+ot) b(t+8t)/6=b(t+81)/6+cAa(t+8t) 振华制 10/14/2013 第七章-2MD方法 18 造

李 振 华 制 10/14/2013 第七章-2 MD 方法 18 造 Predictor-Corrector integration methods (Gear, 1971)  利用Taylor展开式计算下一时刻的位置，速度，加 速度及其它高级项  把实际计算a c (t+δt)的与预测的a(t+δt)作比较 (t t) (t t) (t t) c a   a  a  ( )/ 6 ( )/ 6 ( ) ( )/ 2 ( )/ 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3 2 1 0 t t t t c t t t t t t c t t t t t t c t t t t t t c t t c c c c                                     b b a a a a v v a r r a

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material Predictor-Corrector integration methods(Gear,1971) Gear给出了一套他认为最好的系数 这些系数Taylor阶数的截断阶数有关，这里（三阶 后截断) Co=1/6 C1=5/6 C2=1/2 C3=1/3 李振华 10/14/2013 第七章-2MD方法 19 造

李 振 华 制 10/14/2013 第七章-2 MD 方法 19 造 Predictor-Corrector integration methods (Gear, 1971)  Gear 给出了一套他认为最好的系数 这些系数Taylor阶数的截断阶数有关，这里（三阶 后截断） 1/ 3 1/ 2 5 / 6 1/ 6 3 2 1 0     c c c c

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material 90 其它高阶方法 Runge-Kutta Integrator ■ Bulirsch-Stoer Integrator 振华制 10/14/2013 第七章-2MD方法 20造

李 振 华 制 10/14/2013 第七章-2 MD 方法 20 造 其它高阶方法  Runge-Kutta Integrator  Bulirsch-Stoer Integrator