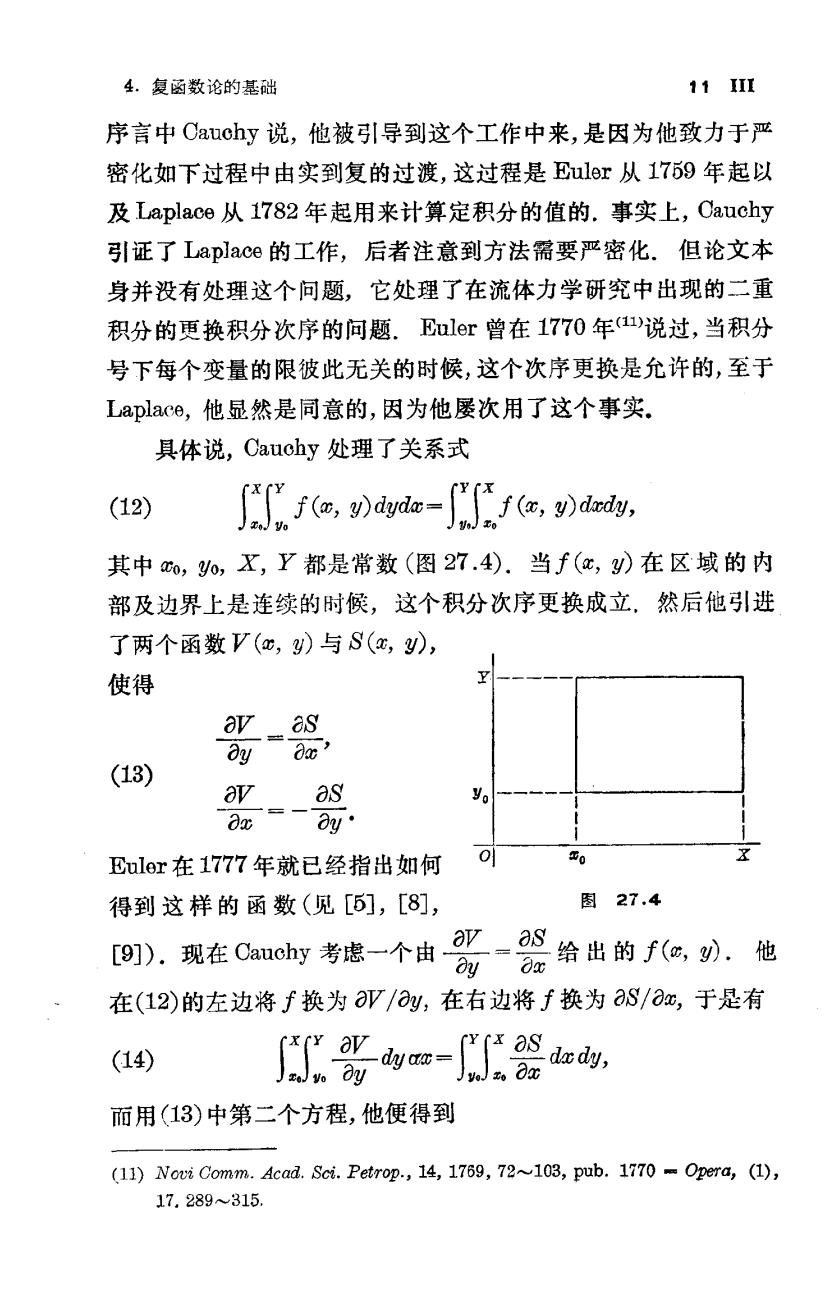
4.复函数论的基础 111 序言中Cauchy说,他被引导到这个工作中来,是因为他致力于严 密化如下过程中由实到复的过渡,这过程是mlr从179年起以 及Laplace从1782年起用来计算定积分的值的.事实上,Cauchy 引证了Laplace的工作,后者注意到方法溶要严密化.但论文本 身并没有处理这个问题,它处理了在流体力学研究中出现的二重 积分的更换积分次序的问题.加ler曾在1770年说过,当积分 号下每个变量的限彼此无关的时候,这个次序更换是允许的,至于 Laplace,他显然是同意的,因为他屡次用了这个事实. 具体说,Cauchy处理了关系式 (12) fo.dvde-)uwds. 其中,o,X,Y都是常数(图27.4).当f(x,)在区域的内 部及边界上是连续的时候,这个积分次序更换成立,然后他引进 了两个函数V(o,)与S(,y), 使得 av as y-0 (13) 器 ulor在1777年就已经指出如何 得到这样的函数(见[5],[8], 图27.4 .我在Cy考虑-个由部-部给出的于小.他 在(12)的左边将f换为aP/,在右边将f换为aS/m,于是有 (14) %m=器, 而用(13)中第二个方程,他便得到 (11)Novi Comm.Acad.Sci.Petrop.,14,1769,72~103,pub.1770-Opera,(1), 17.289315

I112 第27章单复变函数 (15) -瓜器 这些等式可以用来在任一次序下计算二重积分的值.不过它们并 不涉及复函数.当Cauchy在他的引言12中说,他将“严格地并且 直接地建立由实到虚(复)的过渡”时,他心中想的是方程(13). Cauchy说1)这两个方程包含了由实到虚的过渡的全部理论. 上述一切都是在1814年的论文的正文中,而且确实没有明显 指出复函数理论怎样被包括在内.另外,虽然Cauchy按照Euler 与Laplace的同一方式,用复函数来计算实定积分的值,但是这个 用法并未把复函数作为基本实体.一直到1821年,在他的《分析 教程》(Coursd'analyse)中a4),他说 cosa+-Isin a, cosb+√/-1sinb, cos(a+6)+v-Isin(a+b) “是三个符号式,它们不能按照一般已建立的常规来解释,并且不 代表任何实的东西.”他说,上面的第一与第二式的乘积等于第三 式这一事实,并不具有什么意义.为了使这个方程具有意义,必须 令实部与√一工的系数相等.“每一个虚方程仅仅是实量间的两 个方程的符号表示.”如果我们按照对实量建立的法则来对复式进 行运算,我们得到时常是重要的准确结果 在这本书里他确实处理了复数及复变数u+√一1”,其中6 及)是一个实变数的函数,不过总是这样理解,即两个实的部分是 它们的有意义内容.一个复变数的复值函数没有被考虑. 在1822这-一年,Cauchy前进了几步.从关系式(14)和(1) 他有 (12)Eure8,(1),1,330. (13)Ewe3,(L),1,338. (14)Bure,(②),3,154

4.复函数论的基础 13n (V(Y)-V(.]d -[8(x,》-s,g0]y, (17)[S(a,Y)-S(a,v)lda =-x,g-va,0]迪. 现在他有了可以把这两个方程结合起来的想法,因此作出了关于 F(z)=F(o+)=S+训的一个陈述.例如,他以元乘(16)并将 两方程相加,得到 re+na-re+s恤 P(X+》迪-Fa+, 整理后,就给出 (18) Y()d)da -便re+ods+r(x+0, 最后这个结果是沿着一个长方形边界(图27.4)的复积分法这一 简单情形下的Cauchy积分定理.这个结果可以表示为 (19) Jmed-jR肉 ·即是说,积分与路径无关. 以上这些想法,是Cauchy在1822年的一个注解中,在他 《关于无穷小计算误程的总结》as)(Resume des leons sur le calcul in finitesimal)中,并且在1827年发表的1814年的论文的一个脚 注中给出的.从这些较晚的著作,我们看到Cauchy是怎样从实 函数到复函数的. 1825年,Cauchy写了另一篇论文,“关于积分限为虚数的定 (15)-Euvres(2),4,13~256

11114 第27章单复变函数 积分的报告”,但这篇文章到1874年才发表.(a16)这篇论文被许多 人看作是他的最重要的论文,并且是科学史上最瑰丽的一篇,虽然 在一段时间内Cauchy本人并没有赏识到它的价值. 在这篇论文中,他又考虑了将常数及变数用复值代替的方法 来计算实积分的问题.他处理了 (20) fx+ir ()dz 其中z=x+必,并且小心地定义这个积分为和数 [.+) 的极限,其中o,,…,X以及yo,y1,Y是沿着从(,0) 到(X,y)的路径的分划点.这里心十侧肯定是复平面上的一个 点并且积分是沿着一条复的路径的.他还证明,如果令=中(), y=中(),其中t是实的,那么结果与中和中的选择无关,也就是 说,与路径无关,条件是在两条不同的路径之间没有()的间断 点.这个结果普遍化了对于矩形成立的结果. Cauchy正式叙述他的定理如下:若f(m+iy)对于o≤r≤X 和%≤y≤Y为有穷并连续,那末积分(20)的值与函数x=中(t)和 则=()的形式无关.他证明这条定理用了变分的方法.他考虑了 一条可供选择的路径中(t)+u(),中(t)十v(),并且证明积分 对于8的第一变分等于零.这个证明并不令人满意.在其中 Cauchy不仅用了f(2)的导数的存在性,而且还用了导数的连续 性,但他在定理的叙述中并没有作任何假定.对这一点的解释是, Cauchy相信一个连续函数总是可微的,而导数只能在函数本身不 连续的地方才不连续.Cauchy的信念是有道理的,因为在他的工 作的早期,他和十八世纪和十九世纪初期的其他的人一样,都把函 数理解为一个解析表达式,因而导数立即可以通过惯用的形式微 (16)13i.des Sci..Hath,7,1874,265~304,ad8,1875,4355,148~159;this paper is ot in Cauchy's Evvres

4.复函数论的基础 15111 分法则得出. 在1825年的论文中,Cauchy对于他在1814年的论文中以 及在该论文的一个脚注里已经接触到的一个较重要的概念看得较 清楚些了.他考虑当f()在矩形(图27.4)的内部或边界上不连 续时,将发生什么事情.这时沿着两条不同路径的积分的值可能 不同.如果在=a+动处,f(2)为无穷,但极限 F=lim(2-)f(2) 存在,也就是说,在处于有一个单极点,那末积分的差是 士2m√-1F.例如对于函数f(2)=1/(1+),它在:=√-1处 为无穷,因而a=0,b=1,而 ((21) x+(划-1)√-1 -贤e+g*-4g-司 2 Cauchy在他的数学练习》a)(Exercices de mathematique)中,把 量F本身称为积分留数.另外,当一个函数在两条积分路径所围 的区域内有几个极点时,Cauchy指出,必须取留数之和来得到沿 着两条路径的积分之差.在这个关于留数的特别的一节中,他的 两条路径仍构成一个矩形,但他取了很大的一个,并让边长变为无 穷,使所有的留数都包含在内. 在《练习》18)中,Cauchy指出f(z)在:1的留数也是f()展为 2一4的幂级数展开式中项2-)2的系数.很久以后,在1841 年的一篇论文u)中,Cauchy给出了在一个极点的留数的一个新 的表达式,即 Fe0-sTel=∫fO出 (17)Four vol1s,1826~1830-Euvres,(2),6~9. (18)Vol.1,1826,23~37=Eure,(2),6,23~37. (19)Exercices d'analyse et de physique mathsmalique,Vol.2,1841,48~112 Euvre8,(②),12,48~112