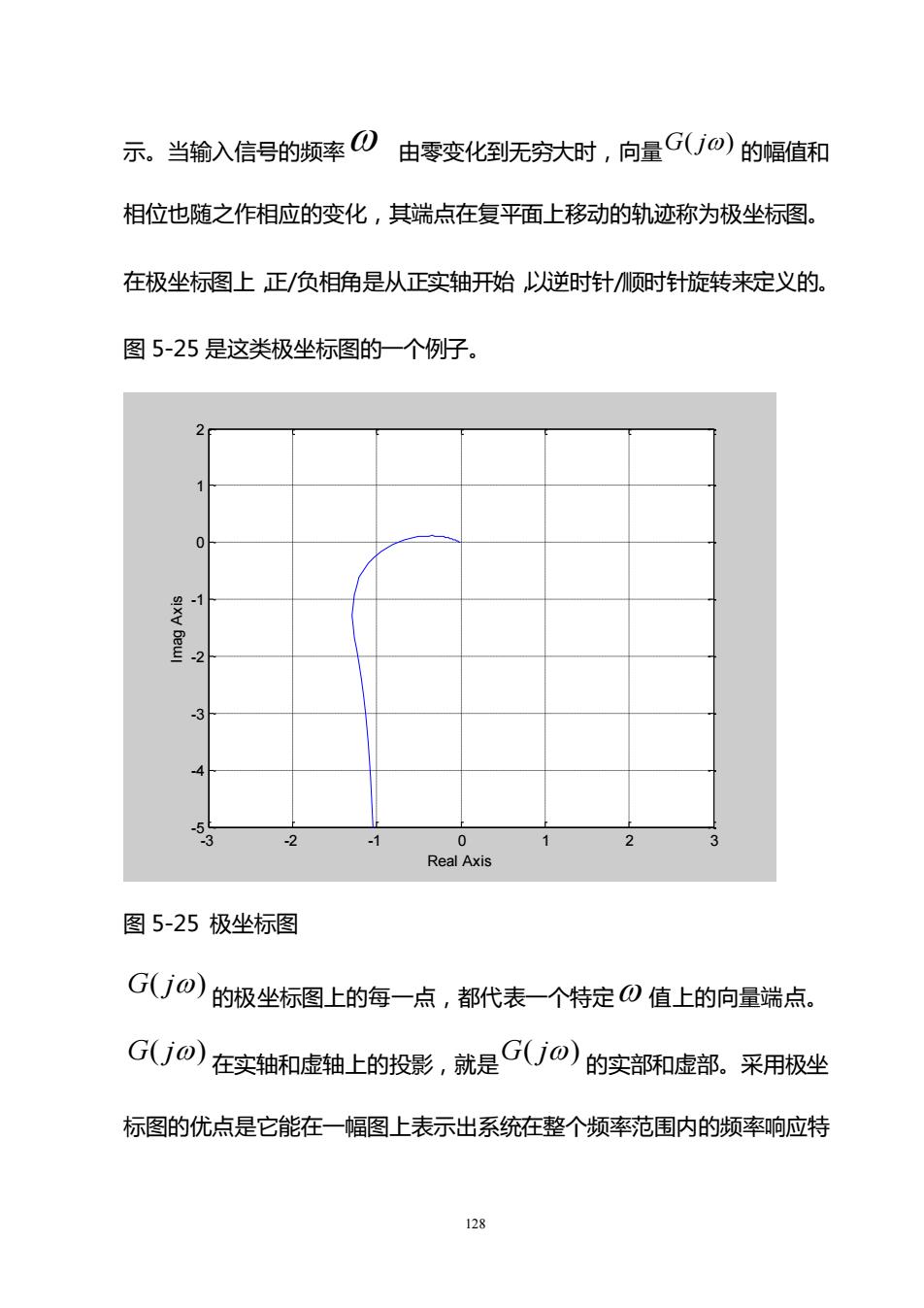
示。当输入信号的频率の由零变化到无穷大时,向量G(jo)的幅值和相位也随之作相应的变化,其端点在复平面上移动的轨迹称为极坐标图。在极坐标图上正/负相角是从正实轴开始以逆时针/顺时针旋转来定义的。图5-25是这类极坐标图的一个例子。0EaxyBeul--3d68-20211RealAxis图5-25极坐标图G(jo)的极坐标图上的每一点,都代表一个特定の 值上的向量端点。G(jo)在实轴和虚轴上的投影,就是G(jo))的实部和虚部。采用极坐标图的优点是它能在一幅图上表示出系统在整个频率范围内的频率响应特128
128 示。当输入信号的频率 由零变化到无穷大时,向量 G( j) 的幅值和 相位也随之作相应的变化,其端点在复平面上移动的轨迹称为极坐标图。 在极坐标图上,正/负相角是从正实轴开始,以逆时针/顺时针旋转来定义的。 图 5-25 是这类极坐标图的一个例子。 -3 -2 -1 0 1 2 3 -5 -4 -3 -2 -1 0 1 2 Real Axis Imag Axis 图 5-25 极坐标图 G( j) 的极坐标图上的每一点,都代表一个特定 值上的向量端点。 G( j) 在实轴和虚轴上的投影,就是 G( j) 的实部和虚部。采用极坐 标图的优点是它能在一幅图上表示出系统在整个频率范围内的频率响应特
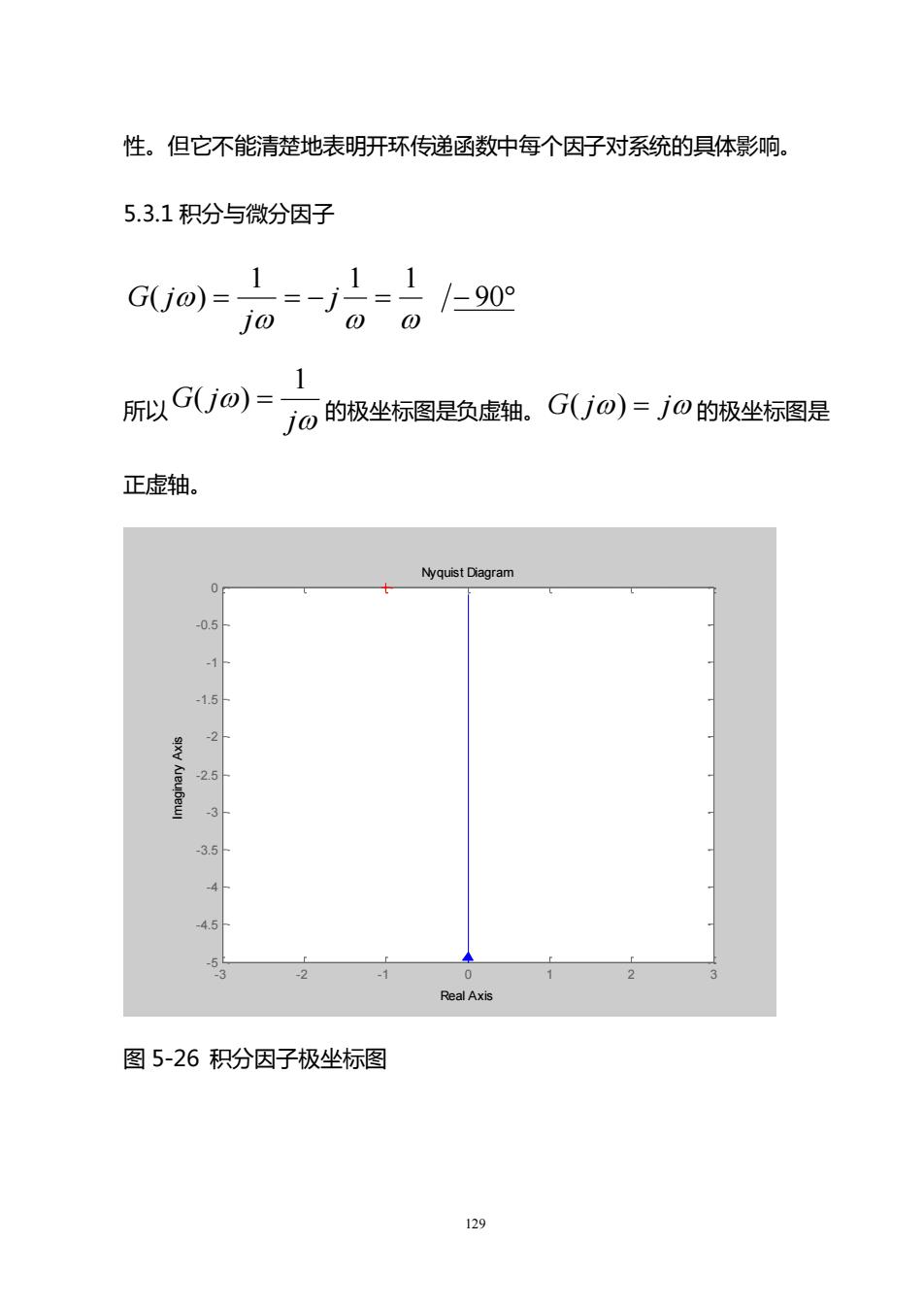
性。但它不能清楚地表明开环传递函数中每个因子对系统的具体影响。5.3.1积分与微分因子11190°G(jo) :jo00所以 G(jの)jn 的极坐标图是负虚轴。G(jo)=jO 的极坐标图是正虚轴。Nyquist Diagram0.5-1-1.5-2r-2.5-33.5A-4.553aRealAxis图5-26积分因子极坐标图129
129 性。但它不能清楚地表明开环传递函数中每个因子对系统的具体影响。 5.3.1 积分与微分因子 = = − = − 90 1 1 1 ( ) j j G j 所以 j G j 1 ( ) = 的极坐标图是负虚轴。 G( j) = j 的极坐标图是 正虚轴。 Nyquist Diagram Real Axis Imaginary Axis - 3 - 2 - 1 0 1 2 3 - 5 -4.5 - 4 -3.5 - 3 -2.5 - 2 -1.5 - 1 -0.5 0 图 5-26 积分因子极坐标图
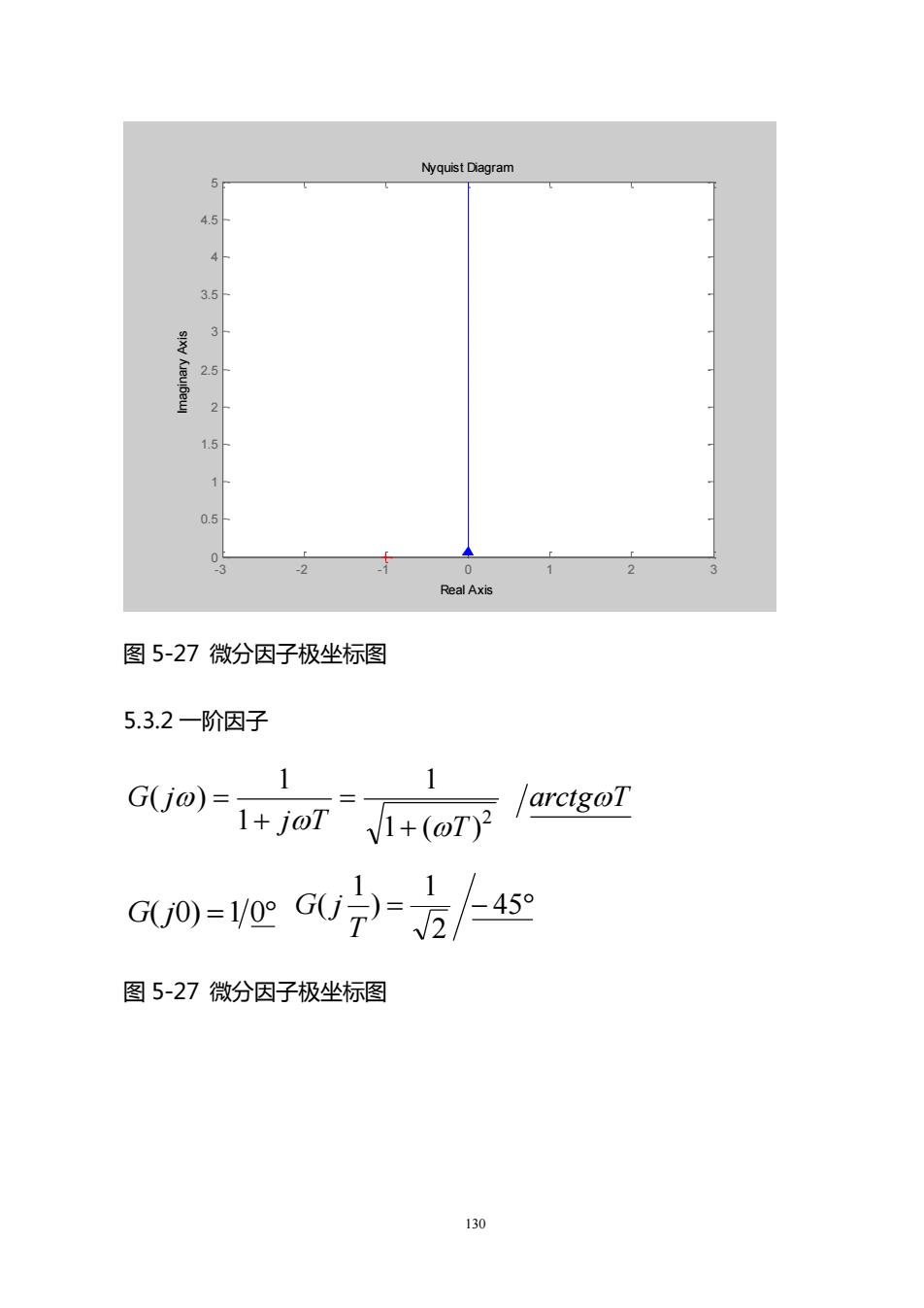
NyquistDiagram4.5A3.53s(xy Kieuibeu2.521.50.5032Real Axis图5-27微分因子极坐标图5.3.2一阶因子11larctgoTG(jo) =1+joT/1+(oT)/45G(j0)=1/0° G(j=)2图5-27微分因子极坐标图130
130 Nyquist Diagram Real Axis Imaginary Axis - 3 - 2 - 1 0 1 2 3 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 图 5-27 微分因子极坐标图 5.3.2 一阶因子 arctg T j T T G j 2 1 ( ) 1 1 1 ( ) + = + = G( j0) =1 0 = − 45 2 1 ) 1 ( T G j 图 5-27 微分因子极坐标图
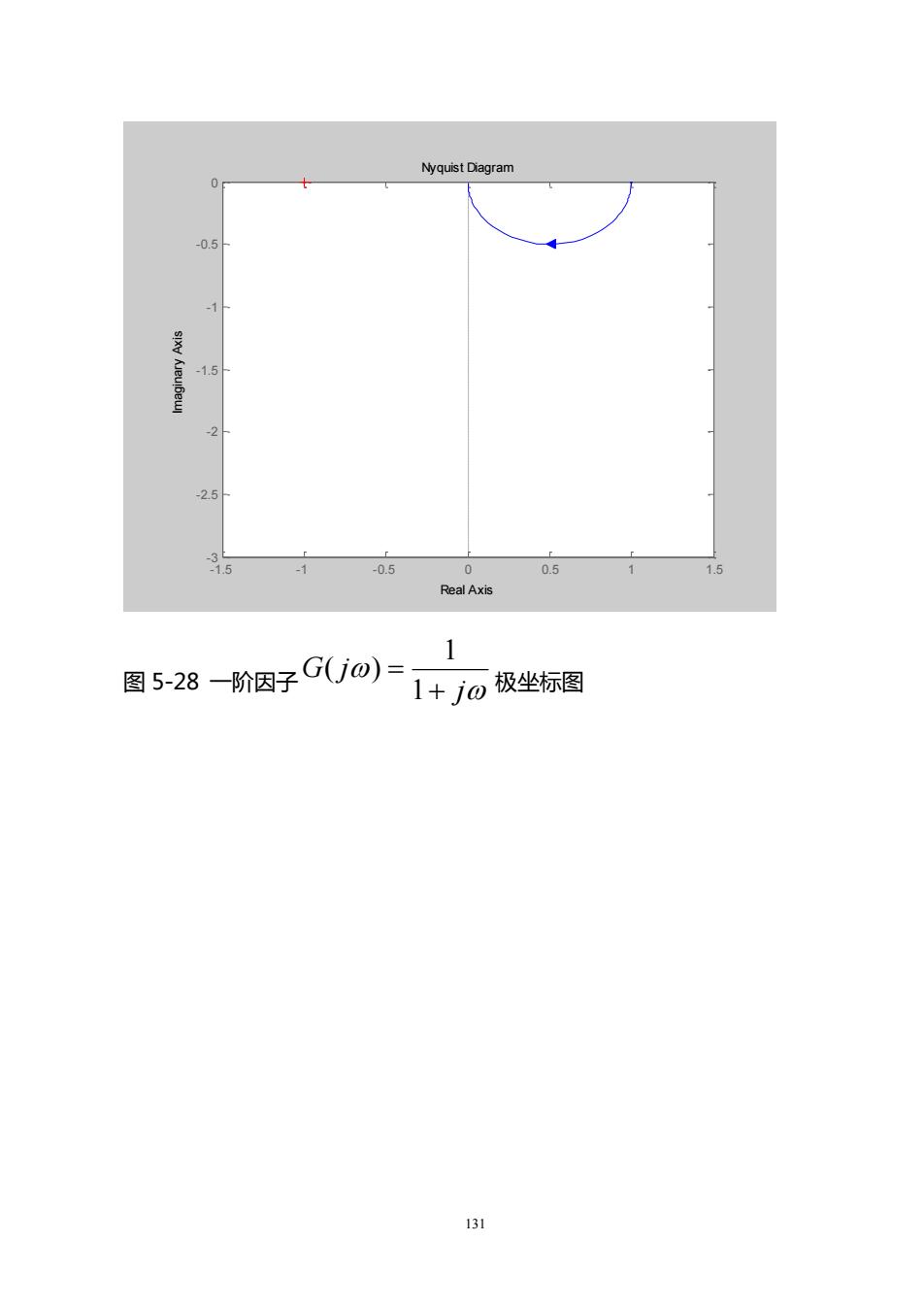
NyquistDiagram10.5-1sx-1.5-2H-2.53-1.50.5-100.51.5Real Axis图 5-28 一阶因子G(jo)=1+jの极坐标图131
131 Nyquist Diagram Real Axis Imaginary Axis -1.5 - 1 -0.5 0 0.5 1 1.5 - 3 -2.5 - 2 -1.5 - 1 -0.5 0 图 5-28 一阶因子 j G j + = 1 1 ( ) 极坐标图
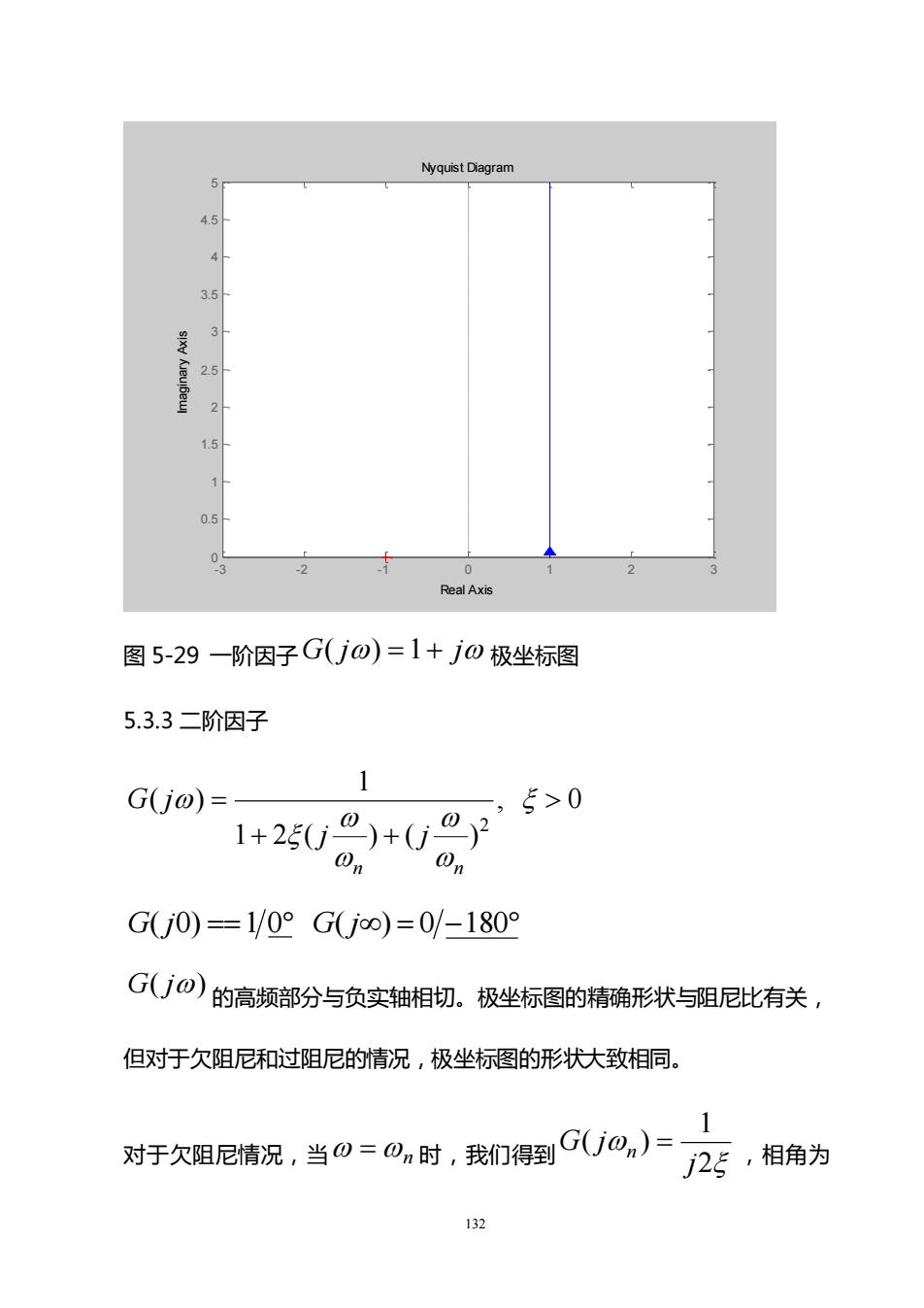
NyquistDiagram4.53.5xeue251.50.5RealAxis图5-29一阶因子G(jの)=1+jの极坐标图5.3.3二阶因子1G(jの) =>C1 + 2E(i1QG(j0) == 1/0° G(joo)= 0/-180°G(jo)的高频部分与负实轴相切。极坐标图的精确形状与阻尼比有关,但对于欠阻尼和过阻尼的情况,极坐标图的形状大致相同。对于欠阻尼情况,当の=のn时,我们得到G(jo,)j2,相角为132
132 Nyquist Diagram Real Axis Imaginary Axis - 3 - 2 - 1 0 1 2 3 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 图 5-29 一阶因子 G( j) =1+ j 极坐标图 5.3.3 二阶因子 , 0 1 2 ( ) ( ) 1 ( ) 2 + + = n n j j G j G( j0) ==1 0 G( j) = 0 −180 G( j) 的高频部分与负实轴相切。极坐标图的精确形状与阻尼比有关, 但对于欠阻尼和过阻尼的情况,极坐标图的形状大致相同。 对于欠阻尼情况,当 =n 时,我们得到 2 1 ( ) j G j n = ,相角为