
入信号,控制系统是否存在稳态误差,以及稳态误差的大小,都可以从观察对数幅值曲线的低频区特性予以确定。①静态位置误差常数的确定E(s)R(s) +C(s)G(s)图5-21单位反馈控制系统考虑图5-21所示的单位反馈控制系统。假设系统的开环传递函数为K(Ts+1)(T2s + 1)..(Tms+ I)G(s) =s'(Tis + 1)(T2s+ 1)..(Tn-vs + 1)K(T j@+1)(T j@ +1)..(Tm j@ +1)G(jo) :(jの)(Tjの+1)(T2j0 +1)..(Tn-vjの+1)图5-22为一个0型系统对数幅值曲线的例子。在这个系统中,G(jo)在低频段等于K,即lim G(jo)= Kp0-0由此得知,低频渐近线是一条幅值为20logKp分贝的水平线。15G(s) =(s + 1)(0.2s + 1)123
123 入信号,控制系统是否存在稳态误差,以及稳态误差的大小,都可以从观 察对数幅值曲线的低频区特性予以确定。 静态位置误差常数的确定 + - R(s) E(s) C(s) G(s) 图 5-21 单位反馈控制系统 考虑图 5-21 所示的单位反馈控制系统。假设系统的开环传递函数为 ( 1)( 1) ( 1) ( 1)( 1) ( 1) ( ) 1 2 1 2 + + + + + + = − s T s T s T s K T s T s T s G s n m ( ) ( 1)( 1) ( 1) ( 1)( 1) ( 1) ( ) 1 2 1 2 + + + + + + = − j T j T j T j K T j T j T j G j n m 图 5-22 为一个 0 型系统对数幅值曲线的例子。 在这个系统中, G( j) 在低频段等于 K p ,即 Kp G j = → lim ( ) 0 由此得知,低频渐近线是一条幅值为 K p 20log 分贝的水平线。 ( 1)(0.2 1) 15 ( ) + + = s s G s
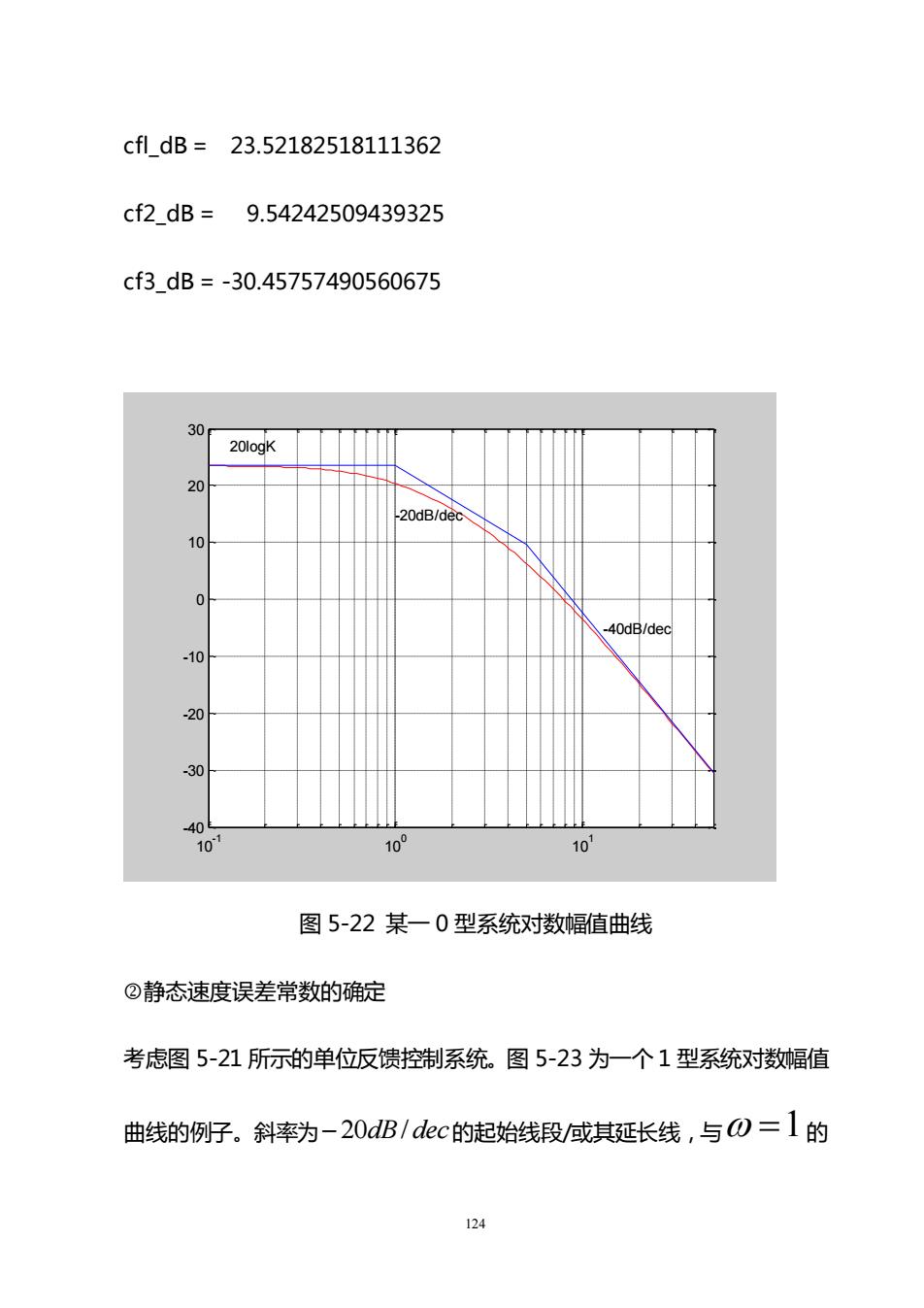
cfl_dB=23.52182518111362cf2 dB =9.54242509439325cf3dB=-30.457574905606753020logk20-20dB/dec100-40dB/dec-10-20-30-4010°10~110图5-22某一0型系统对数幅值曲线②静态速度误差常数的确定考虑图5-21所示的单位反馈控制系统。图5-23为一个1型系统对数幅值曲线的例子。斜率为-20dB/dec的起始线段/或其延长线,与の=1 的124
124 cfl_dB = 23.52182518111362 cf2_dB = 9.54242509439325 cf3_dB = -30.45757490560675 10-1 100 101 -40 -30 -20 -10 0 10 20 30 20logK -20dB/dec -40dB/dec 图 5-22 某一 0 型系统对数幅值曲线 静态速度误差常数的确定 考虑图 5-21 所示的单位反馈控制系统。图 5-23 为一个 1 型系统对数幅值 曲线的例子。斜率为−20dB/ dec 的起始线段/或其延长线,与 =1 的

直线的交点具有的幅值为20logK,。这可证明如下:K在 1 型系统中G(jの)=0<<1jo=20logK,斜率为-20dB/dec的起始线段/或其因此20log0=延长线与0 分贝线的交点的频率在数值上等于K,。假设交点上的频率为K01,于是即joK作为一个例子,考虑具有单位反馈的1型系统,其开环传递函数为:KG(s) =s(Ts + 1)如果定义转角频率为の2,假设斜率为-40dB/dec的直线与/或其延长线1K20302,0 =K, = K与0分贝线的交点为の3TT由此得到 2 =01_03即302在伯德图上, log O1 - log 0 = log 03 -log 2125
125 直线的交点具有的幅值为 Kv 20log 。这可证明如下: 在 1 型系统中 ( ) = , 1 j K G j v 因此 v v K j K 20log 20log 1 1 = = 斜率为 −20dB/ dec 的起始线段/或其 延长线与 0 分贝线的交点的频率在数值上等于 Kv 。假设交点上的频率为 1 ,于是 1 1 = j Kv 即 Kv =1 作为一个例子,考虑具有单位反馈的 1 型系统,其开环传递函数为: ( 1) ( ) + = s Ts K G s 如果定义转角频率为 2 ,假设斜率为−40dB/ dec 的直线与/或其延长线 与 0 分贝线的交点为 3 , T 1 2 = , T K = 2 3 ,1 = Kv = K 由此得到 2 1 2 =3 即 2 3 3 1 = 在伯德图上, 1 3 3 2 log −log = log −log
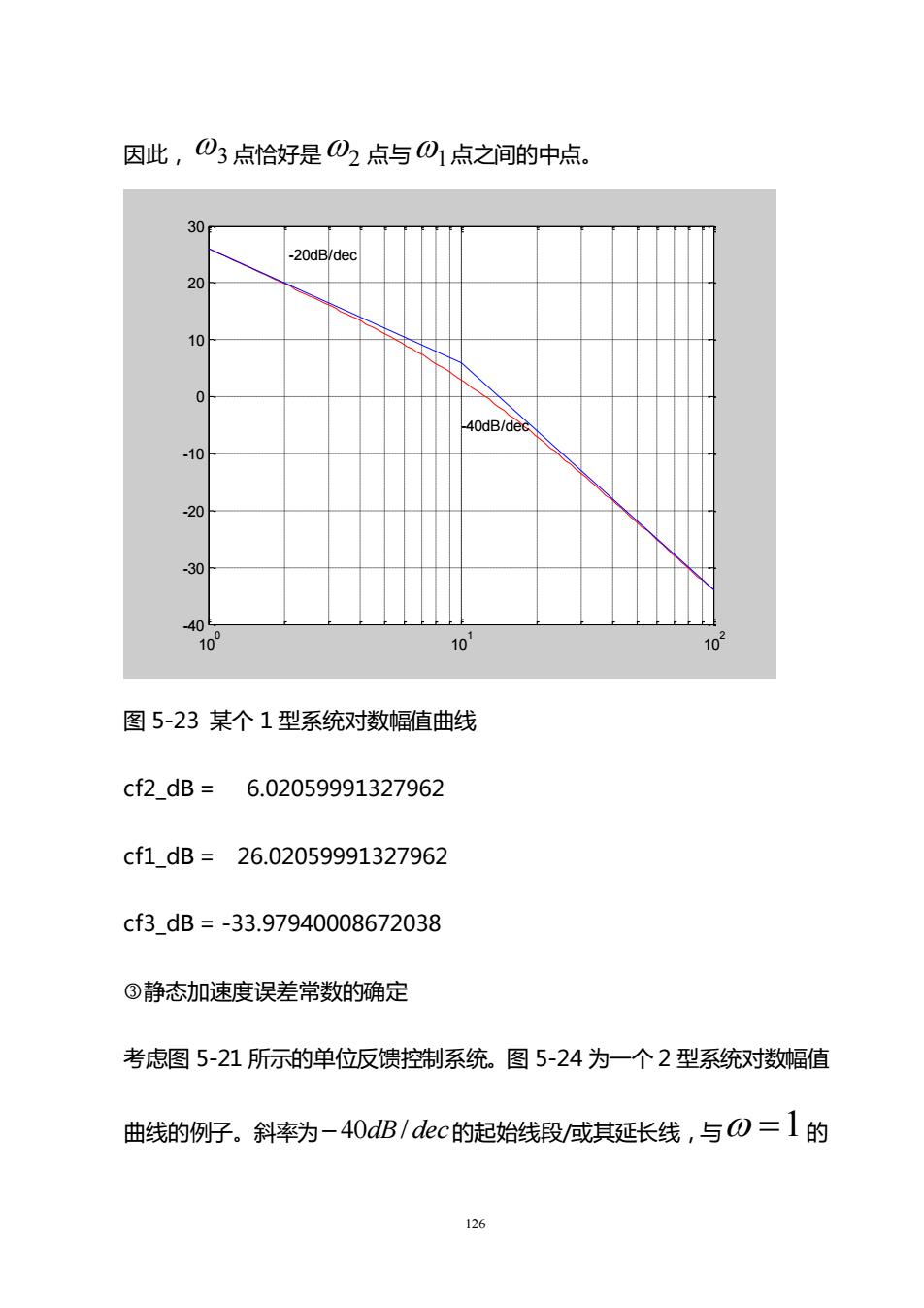
因此,①3点恰好是2点与01点之间的中点。30-20dB/dec20100-40dB/dee-10-20-30-401001010图5-23某个1型系统对数幅值曲线cf2_dB =6.02059991327962cf1 dB=26.02059991327962cf3_dB=-33.97940008672038③静态加速度误差常数的确定考虑图5-21所示的单位反馈控制系统。图5-24为一个2型系统对数幅值曲线的例子。斜率为-40dB/dec的起始线段/或其延长线,与の=1 的126
126 因此, 3 点恰好是 2 点与 1 点之间的中点。 100 101 102 -40 -30 -20 -10 0 10 20 30 -20dB/dec -40dB/dec 图 5-23 某个 1 型系统对数幅值曲线 cf2_dB = 6.02059991327962 cf1_dB = 26.02059991327962 cf3_dB = -33.97940008672038 静态加速度误差常数的确定 考虑图 5-21 所示的单位反馈控制系统。图 5-24 为一个 2 型系统对数幅值 曲线的例子。斜率为−40dB/ dec 的起始线段/或其延长线,与 =1 的

直线的交点具有的幅值为20logK。Ka0<<1G(io)由于低频时(jo)?K20log= 20log K所以(jo)斜率为-40dB/dec的起始线段/或其延长线与0分贝线的交点的频率为のa在数值上等于 K。α的平方根。证明如下:K.20log1=0于是=/K20log(joa)dB A-40dB/dec-60dB/dec-20dB/decの(对数坐标)C00a=Ka0=1图5-242型系统对数幅值曲线5.3极坐标图(Polarplot),幅相频率特性曲线,奈奎斯特曲线G(jo)G(jの)可用幅值和相角 (の)的向量表频率特性是复数。127
127 直线的交点具有的幅值为 Ka 20log 。 由于低频时 , 1 ( ) ( ) 2 = j K G j a 所以 a a K j K 20log ( ) 20log 1 2 = = 斜率为 −40dB/ dec 的起始线段/或其延长线与 0 分贝线的交点的频率为 a 在数值上等于 Ka 的平方根。证明如下: 20log1 0 ( ) 20log 2 = = a a j K 于是 a = Ka ( 对数坐标 ) dB −40dB/dec −60dB/dec −20dB/dec =1 0 a = Ka 图 5-24 2 型系统对数幅值曲线 5.3 极坐标图(Polar plot),幅相频率特性曲线,奈奎斯特曲线 频率特性是复数。 G( j) 可用幅值 G( j) 和相角 () 的向量表